【模式识别与机器学习】——PCA与Kernel PCA介绍与对比

 

PCA与Kernel PCA介绍与对比

1. 理论介绍

　　PCA：是常用的提取数据的手段，其功能为提取主成分（主要信息），摒弃冗余信息（次要信息），从而得到压缩后的数据，实现维度的下降。其设想通过投影矩阵将高维信息转换到另一个坐标系下，并通过平移将数据均值变为零。PCA认为，在变换过后的数据中，在某一维度上，数据分布的更分散，则认为对数据点分布情况的解释力就更强。故在PCA中，通过方差来衡量数据样本在各个方向上投影的分布情况，进而对有效的低维方向进行选择。

　　KernelPCA：是PCA的一个改进版，它将非线性可分的数据转换到一个适合对齐进行线性分类的新的低维子空间上，核PCA可以通过非线性映射将数据转换到一个高维空间中，在高维空间中使用PCA将其映射到另一个低维空间中，并通过线性分类器对样本进行划分。

　　核函数：通过两个向量点积来度量向量间相似度的函数。常用函数有：多项式核、双曲正切核、径向基和函数（RBF）（高斯核函数）等。

2. 技术实现

　　（1）在KernelPCA中，这个问题同样是求特征向量的问题，只不过目标矩阵是经过核变换之后的协方差矩阵；与前相同，这个问题解决的实质还是要求C矩阵的特征向量，但对C求特征向量的过程较为复杂，经过了几次矩阵变化，先求得与核变换有关的矩阵K 的特征向量a，再通过变换方程与a的点乘得到协方差矩阵的特征向量v。

 

　　（2）Kernel版的PCA思想是比较简单的，我们同样需要求出Covariance matrix C，但不同的是这一次我们要再目标空间中来求，而非原空间。

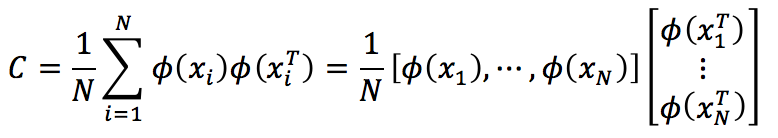
如果令，则Φ(_i)表示_i被映射到目标空间后的一个列向量，于是同样有

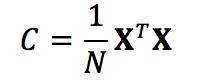
C和X^TX具有相同的特征向量。但现在的问题是Φ是隐式的，我们并不知道。所以，我们需要设法借助核函数K来求解X^TX。

因为核函数K是已知的，所以XX^T是可以算得的。

 

 

 

　　（3）扼要总结如下：

Solve the following eigenvalue problem:

 

The projection of the test sample Φ(xj) on the i-th eigenvector can be computed by

 

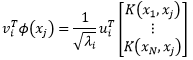
所得之vTi·Φ(xj)即为特征空间（Feature space）中沿着vi方向的坐标。

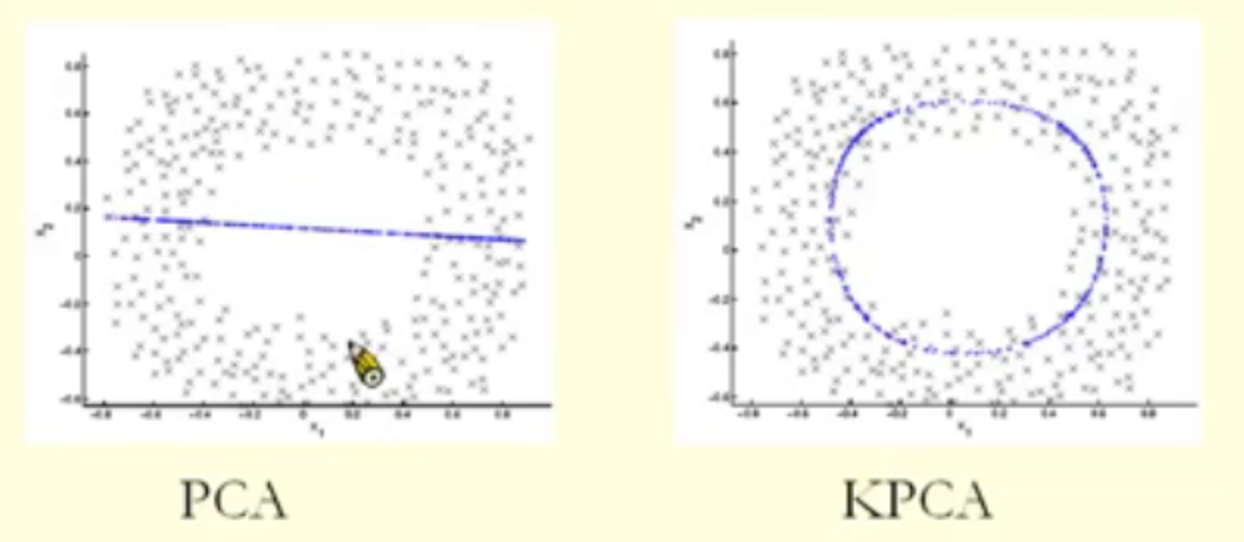
　　（4）最后我们给出的是一个KPCA的例子。其中左图是用传统PCA画出的投影。右图是在高维空间中找到投影点后又转换回原空间的效果。可见，加了核函数之后的PCA变得更加强大了。

 

具体推法：https://blog.csdn.net/zhangping1987/article/details/30492433