DS博客作业05--树
1.本周学习总结
1.1.思维导图
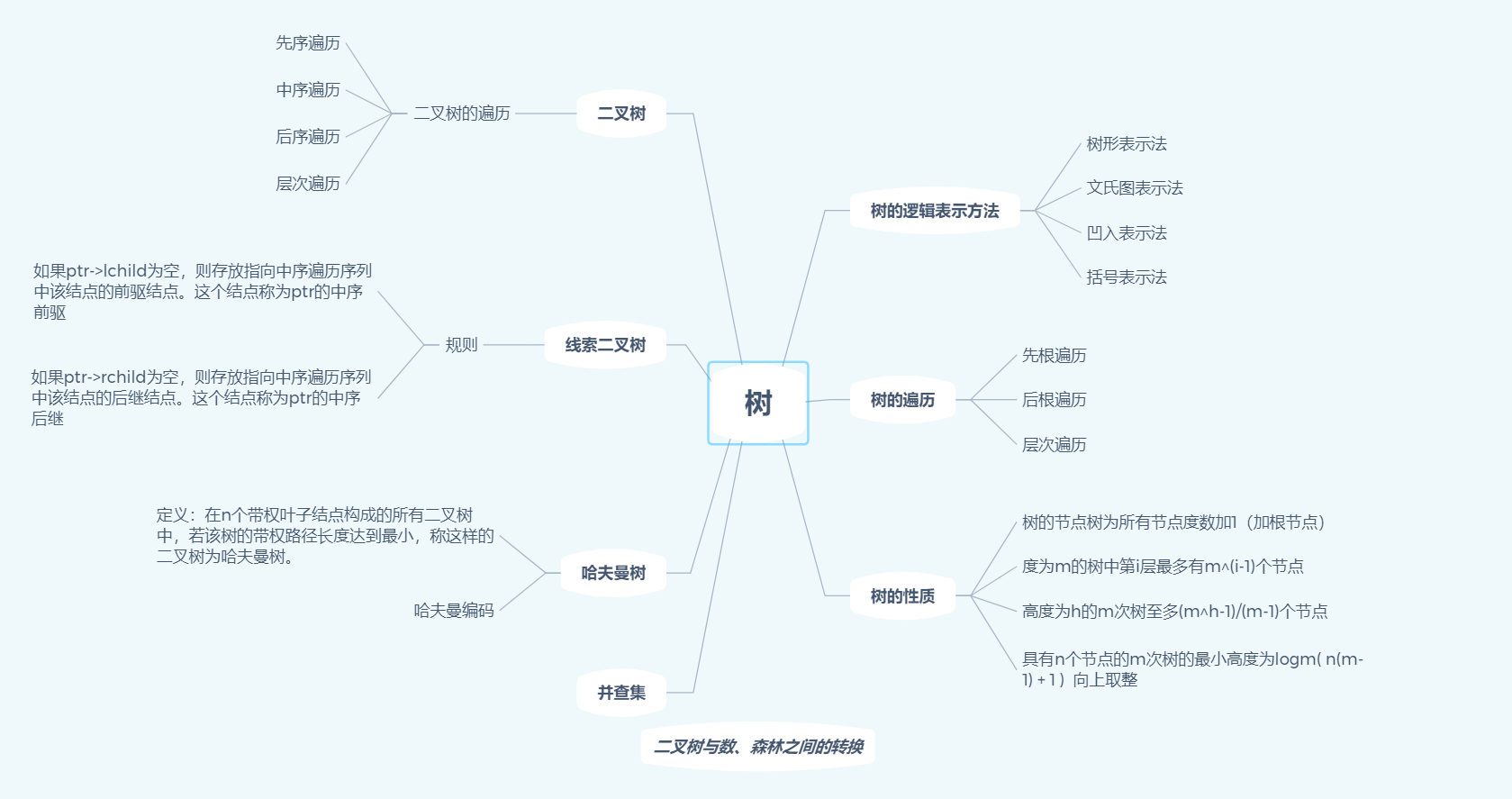
1.2谈谈你对树结构的认识及学习体会
树的学习很难,但也很有意义,学好树,能让我们的代码简洁许多。在学习过程中,多在草稿纸上画图,这样能够帮助理解。对递归计算的理解很重要,但也是最花时间的部分。
2.pta实验作业
2.1题目1:输出二叉树每层节点
2.1.1设计思路
main函数{
定义字符串str;
定义树指针b;
定义 i=0,高度h;
输入str;
b=CreatBtree(str,i);
h=GetHeight(b);
PrintLevel(b,h);
return 0;
}
CreatBtree函数题目已给出;
GetHeight函数略过;
CreatBtree函数
{
定义 i=0,flag=0,k=0;
定义树指针 p;
定义队列指针 q;
if b 为空
输出"NULL";
return;
树的根结点入队b;
输出 “++i:根结点的data,”;
输出 “++i:”;
h=h-2;
if(根结点的左孩子不为空)
将其左孩子入队;
输出左孩子;
k++;
if(根结点的右孩子不为空)
将其右孩子入队;
输出右孩子;
k++;
出队;
while(队不为空)
flag=k;
k=0;
if h不等于0 输出 “++i:”;
while(flag不等于0)
p=队头的结点;
if(根结点的左孩子不为空)
将其左孩子入队;
输出左孩子;
k++;
if(根结点的右孩子不为空)
将其右孩子入队;
输出右孩子;
k++;
出队;
flag--;
if h不等于0 输出换行符;
h--
}
2.1.2代码截图
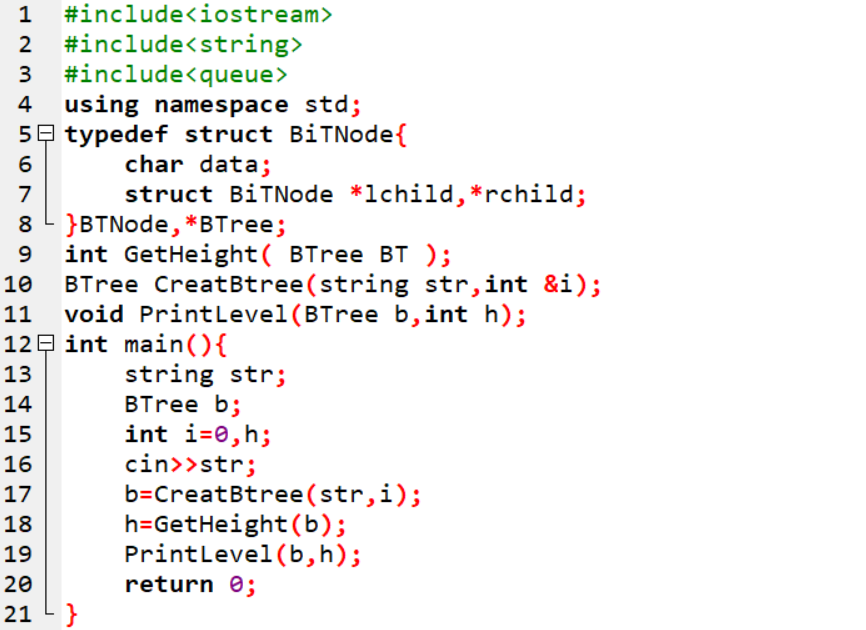


2.1.3PTA提交列表说明

- Q1:刚开始做的时候在如何输出正确格式的答案上花了很多时间。
- A1:添加上了一个计算树的高度的函数就问题解决了。
- Q2:创建树出了问题。
- A2:在函数CreatBtree中的形参i前应加上引用符号&。
2.2题目2:根据后序和中序遍历输出先序遍历
2.2.1设计思路
main函数{
定义树根结点 b=NULL
定义数组post[30],in[30];
定义结点数N,i;
b=new BTNode;
输入N;
for i=0 to i<N
输入post[i];
for i=0 to i<N
输入in[i];
b=CreatBT(post,in,N);
输出"Preorder:";
GetPre(b);
return 0;
}
CreatBT函数{
定义树结点指针 b;
定义整型数 r,k,*p;
if N小等于0 return NULL
r=*(post+N-1);
b=new BTNode;
b->data=r;
for p=in to p<in+N
如果 *p 等于 r break;
k=p-in;
b的左孩子等于CreatBT(post,in,k);
b的右孩子等于CreatBT(post+k,p+1,N-k-1);
return b;
}
GetPre函数{
if b不为空
输出“ ”以及b->data;
GetPre(b的左孩子);
GetPre(b的右孩子);
}
2.2.2代码截图
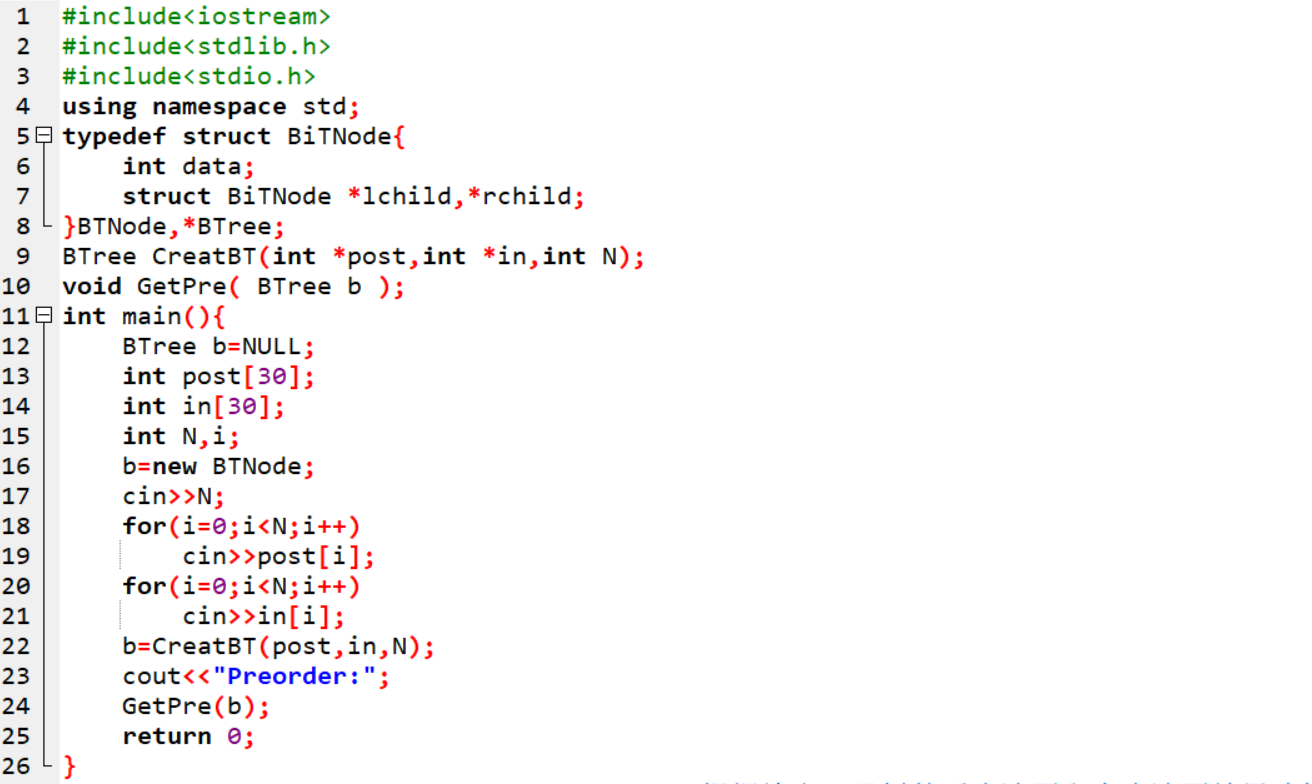
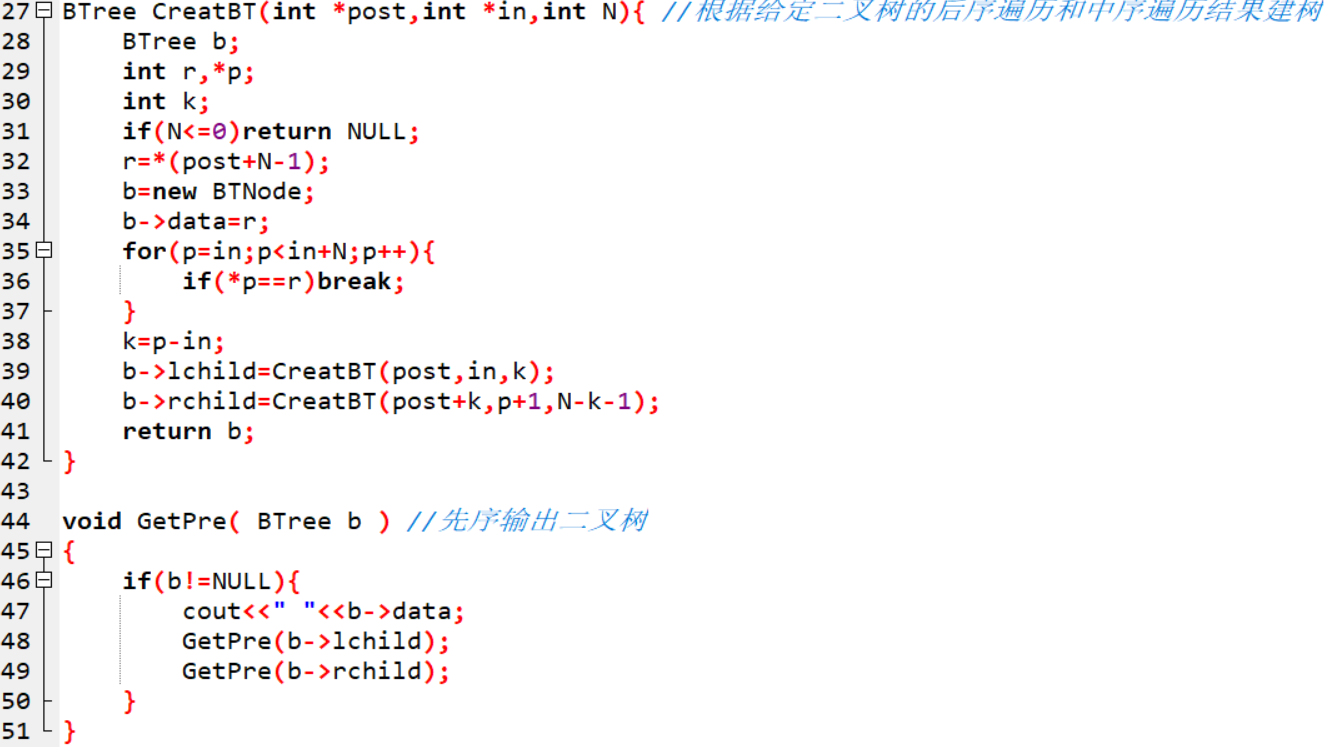
2.2.3PTA提交列表说明

- Q1:测试点一和四发生段错误
- A1:发现是树结点的类型定义错误。
2.3题目3:还原二叉树
2.3.1设计思路
main函数{
定义树结点指针 b;
定义字符数组pre[50],in[50];
定义结点数N;
b=new BTNode;
输入N;
输入pre,in;
b=CreatBT(pre,in,N);
输出GetHeight(b);
return 0;
}
CreatBT函数{
定义树结点指针 b;
定义字符指针 *p;
定义整型数 k;
if N小等于0 return NULL;
b=new BTNode;
b->data=*pre;
for p=in to p<in+N
如果 *p 等于 *pre break;
k=p-in;
b的左孩子等于CreatBT(post+1,in,k);
b的右孩子等于CreatBT(post+k+1,p+1,N-k-1);
return b;
}
GetHeight函数{
定义整型数 lh,rh;
if 结点BT为空 return 0;
else
lh等于GetHeight(BT->lchild);
rh等于GetHeight(BT->rchild);
若lh大于rh,返回lh+1;反之,返回rh+1;
}
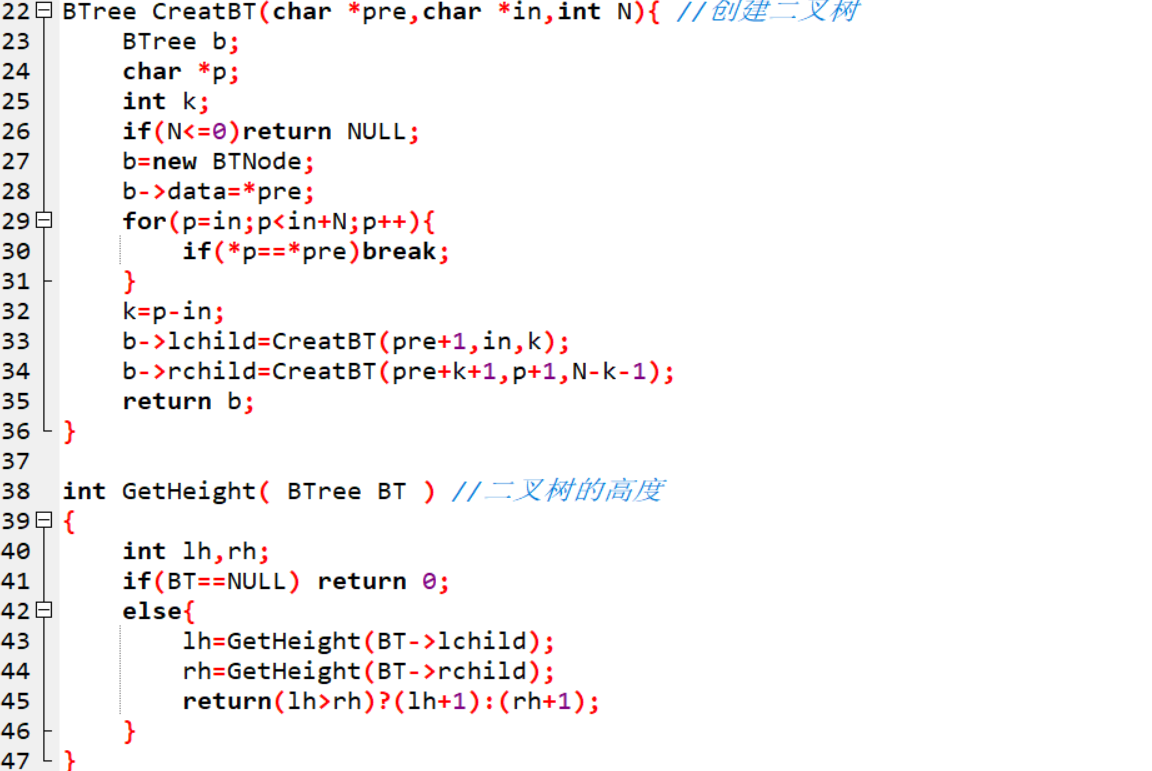
2.3.2代码截图

2.3.3PTA提交列表说明

- 答案正确
3.阅读代码
3.1题目:玩转二叉树
给定一棵二叉树的中序遍历和前序遍历,请你先将树做个镜面反转,再输出反转后的层序遍历的序列。所谓镜面反转,是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。
输入第一行给出一个正整数N(≤30),是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。
3.2解题思路
build函数 //la,ra表示中序遍历 lb,rb表示前序遍历
{
if la大于ra
return 0;
定义整形数 x等于pre[lb];
定义整形数 p1等于la,p2;
while(in[p1]不等于x) //在前序遍历中找到根节点
p1++;
p2等于p1-la;
a[x]的左孩子等于build(la,p1-1,lb+1,lb+p2);
a[x]的右孩子等于build(p1+1,ra,lb+p2+1,rb);
return x;
}
bfs函数
{
定义队列 q;
将先序遍历的根结点入队
定义整型数组 b[55];
定义整型数 k=0;
while(队列不为空) //利用队列来按层输出
{
定义 z等于队头;
出队;
b[k++]等于z;
if a[z]的右孩子不为空
将a[z]的右孩子入队;
if a[z]的左孩子不为空
将a[z]的左孩子入队;
}
for i=0 to k-1
if i等于0 输出“b[i]”;
else 输出“ b[i]”;
return;
}
main()函数
{
定义 n;
输入n;
for i=0 to n-1
输入in[i];
for i=0 to n-1
输入pre[i];
bfs(pre[0]);
return 0;
}
3.3代码截图



3.4学习体会
- 学习到可以使用万能头文件#include<bits/stdc++.h>
- 平时更经常使用二叉链的储存结构进行操作,但本题使用顺序存储结构会更加精简。
- 层次遍历输出的函数值得借鉴。
