对顶堆
最近leetcode上面遇到一道题，需要用滑动窗口维护前k个出现最多的数的区间和，但是用对顶堆可以方便的写出来，下面介绍一种用multiset实现对顶堆的用法
先上模板：
typedef pair<int,int> E;
struct topheap{
int k; //后k个最大值
multiset<E>m1,m2;
void adjust()//调整函数
{
while(m2.size() > k)
{
E p = *m2.begin();
m2.erase(m2.begin());
m1.insert(p);
}
while(m1.size() && m2.size() < k)
{
E p = *prev(m1.end());
m1.erase(prev(m1.end()));
m2.insert(p);
}
}
void add(E p) //增加节点
{
if(p < *m2.begin()) m1.insert(p);
else m2.insert(p);
adjust();
}
void del(E p)
{
auto it = m2.find(p);
if(it != m2.end()) m2.erase(it);
else m1.erase(m1.find(p));
adjust();
}
void print() //打印元素，方便调试
{
if(m2.size())
{
for(auto it = m2.rbegin();it != m2.rend();it ++)
{
E p = *it;
cout<<p.first<<" "<<p.second<<endl;
}
}
if(m1.size())
{
for(auto it = m1.rbegin();it != m1.rend();it ++)
{
E p = *it;
cout<<p.first<<" "<<p.second<<endl;
}
}
}
};
用multiset的好处是可以选择维护前k小的元素集合还是后k大的元素集合，只需要把m1和m2中维护哪一个元素个数是k就行了，前者是前k小，后者是后k大。同时，用multiset还能访问堆顶之外的其他元素。
题目：3321. 计算子数组的 x-sum II
题解代码：
typedef pair<long long,long long> E;
struct topheap{
long long k,sum = 0; //sum用来求后x种数的区间和，这里的k就是维护的元素个数
multiset<E>m1,m2;
void kset(long long x) {k = x;}
void adjust()
{
while(m2.size() > k)
{
E p = *m2.begin();
sum -= p.first * p.second;
m2.erase(m2.begin());
m1.insert(p);
}
while(m1.size() && m2.size() < k)
{
E p = *prev(m1.end());
sum += p.first * p.second;
m1.erase(prev(m1.end()));
m2.insert(p);
}
}
void add(E p)
{
if(p < *m2.begin()) m1.insert(p);
else m2.insert(p),sum += p.first * p.second;
adjust();
}
void del(E p)
{
auto it = m2.find(p);
if(it != m2.end()) m2.erase(it),sum -= p.first * p.second;
else m1.erase(m1.find(p));
adjust();
}
void print()
{
if(m2.size())
{
cout<<"m2:"<<endl;
for(auto it = m2.rbegin();it != m2.rend();it ++)
{
E p = *it;
cout<<p.first<<" "<<p.second<<endl;
}
}
if(m1.size())
{
cout<<"m1:"<<endl;
for(auto it = m1.rbegin();it != m1.rend();it ++)
{
E p = *it;
cout<<p.first<<" "<<p.second<<endl;
}
}
}
};
class Solution {
public:
vector<long long> findXSum(vector<int>& nums, int k, int x) {
int n = nums.size();map<long long,long long> mp;topheap hap;vector<long long> ans;
hap.kset(x);
for(int i = 0;i < k;i ++) mp[nums[i]] ++;
for(auto [x,y] : mp) //初始化，先把下表为0的ans加入答案数组
hap.add({y,x});
ans.push_back(hap.sum);
for(int i = 1;i + k - 1< n;i ++)
{
long long fir = nums[i - 1],sec;
if(mp[fir] > 0)
{
sec = mp[fir];
hap.del({sec,fir});
mp[fir] --;
if(mp[fir] > 0) hap.add({mp[fir],fir}); //如果减去这个位置之前那个数一个的情况下，出现次数不为0
}
fir = nums[i + k - 1],sec = mp[fir];
if(sec > 0) //如果i + k - 1这个位置的数在维护的集合里面出现了，就先把它删除
hap.del({sec,fir});
mp[fir] ++;
hap.add({++sec,fir});
ans.push_back(hap.sum);
}
return ans;
}
};
简单介绍
对顶堆算法最早由美国计算机科学家 罗伯特·弗洛伊德 提出
该算法一般用来动态的维护数据中前K个小的数
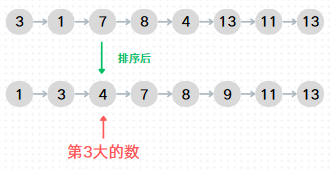
暴力求法
暴力求法就是先将数据排好序然后从第一小的那个数开始，一个一个往后面数，直到数到第K大的数为止
代码实现部分：
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main()
{
int n,k;//n个数，第k大的数
cin>>n;
vector<int> nums(n);
for(int i = 0 ;i < n;i ++) //输入数据
{
cin>>nums[i];
}
sort(nums.begin(),nums.end());//排序
int k;cin>>k;
cout<<nums[k - 1]<<endl;
return 0;
}
这样一旦数据给的多了，要求一边输入数据一边求已有数据里面第k大的数的话就会大大降低程序的效率
对顶堆算法
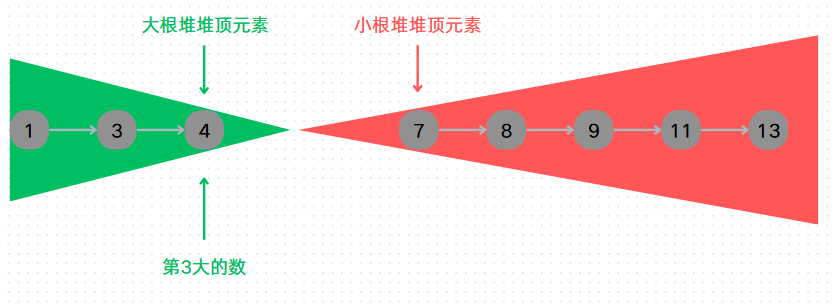
于是我们用到堆来解决这个问题
我们分别用一个大根堆和一个小根堆将堆顶对起来存数据。由于大根堆和小根堆的性质分别是把堆里面的最小值放在堆顶和把堆里面的最大值放在堆顶，所以我们只需要保持小根堆里面的元素个数只有k个就行了。这样一来，小根堆堆顶的元素就是第k大那个元素。
代码实现部分
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
struct DualHeap {
priority_queue<int> minHeap; //大根堆，存前k个数
priority_queue<int,vector<int>,greater<int>> maxHeap; //小根堆，存后面的数
int k = 0; // 要保持小根堆中的元素个数
void k_set(int u) { k = u; }
//调整函数
void adjust() {
while (minHeap.size() > k) {
maxHeap.push(minHeap.top());
minHeap.pop();
}
while (minHeap.size() < k && maxHeap.size()) {
minHeap.push(maxHeap.top());
maxHeap.pop();
}
}
// 插入元素
void add(int u) {
if (minHeap.size() < k || u < minHeap.top()) {
minHeap.push(u);
} else {
maxHeap.push(u);
}
adjust(); // 调整堆平衡
}
int get_k() {
return minHeap.top();
}
};
int main() {
int n, k;
cin >> n >> k;
DualHeap heap;
heap.k_set(k);
for (int i = 0; i < n; i++) {
int x;
cin >> x;
heap.add(x); // 插入每个元素
}
cout << heap.get_k() << endl;
return 0;
}
扩展
我们既可以用对顶堆动态维护前k个数，也可以用对顶堆的性质维护后k个数。
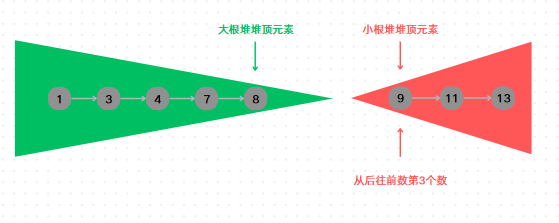
假设我们需要求从后往前数第k个数，暴力做法也是效率很低，这里我们只需要让小根堆的元素个数保持在k个就行了，其他小一点的元素放到大根堆里面就行了。
这里我们当k等于3，也就是按从大到小的顺序的第3个数
代码实现：
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
struct DualHeap {
priority_queue<int> minHeap; //大根堆，存前k个数
priority_queue<int, vector<int>, greater<int>> maxHeap; //小根堆，存后面的数
int k = 0; // 要保持小根堆中的元素个数
void k_set(int u) { k = u; }
//调整函数
void adjust() {
while (maxHeap.size() > k) {
minHeap.push(maxHeap.top());
maxHeap.pop();
}
while (maxHeap.size() < k && minHeap.size()) {
maxHeap.push(minHeap.top());
minHeap.pop();
}
}
// 插入元素
void add(int u) {
if (maxHeap.size() < k || u > maxHeap.top()) {
maxHeap.push(u);
} else {
minHeap.push(u);
}
adjust(); // 调整堆平衡
}
int get_k() {
return maxHeap.top();
}
};
int main() {
int n, k;
cin >> n >> k;
DualHeap heap;
heap.k_set(k);
for (int i = 0; i < n; i++) {
int x;
cin >> x;
heap.add(x); // 插入每个元素
}
cout << heap.get_k() << endl;
return 0;
}
