#啥也不是：飞蛾子乱飞

飞蛾子乱飞

问题(4.5)描述：

正儿八经的复杂做法

极坐标下进行建模

飞蛾1的运动轨迹为：

\[\rho=\rho(\theta) \]

飞蛾2的运动轨迹为：

\[\rho=\rho(\theta+\frac{2}{3}\pi) \]

飞蛾3的运动轨迹为：

\[\rho=\rho(\theta-\frac{2}{3}\pi) \]

根据

\[飞蛾1的轨迹切线方向(朝向)=飞蛾1飞蛾2位置直线方向 \]

建立方程如下：

\[\left\{\frac{\sin (\theta ) \rho'(\theta )+\cos (\theta ) \rho(\theta )}{\cos (\theta ) \rho'(\theta )-\sin (\theta ) \rho(\theta )}=\frac{\sin \left(\theta +\frac{2 \pi }{3}\right) \rho\left(\theta +\frac{2 \pi }{3}\right)-\sin (\theta ) \rho(\theta )}{\cos \left(\theta +\frac{2 \pi }{3}\right) \rho\left(\theta +\frac{2 \pi }{3}\right)-\cos (\theta ) \rho(\theta )}\right\} \]

注意到三只飞蛾飞行轨迹形状完全一致，则有

\[\rho\left(\theta +\frac{2 \pi }{3}\right)=\rho\left(\theta \right) \]

得到以下微分方程：

\[\left\{\frac{\sin (\theta ) \rho '(\theta )+\rho (\theta ) \cos (\theta )}{\cos (\theta ) \rho '(\theta )-\rho (\theta ) \sin (\theta )}=\frac{\rho (\theta ) \sin \left(\theta +\frac{2 \pi }{3}\right)-\rho (\theta ) \sin (\theta )}{\rho (\theta ) \cos \left(\theta +\frac{2 \pi }{3}\right)-\rho (\theta ) \cos (\theta )}\right\} \]

得到其通解为：

\[\rho(\theta)=C\cdot\text e^{-\sqrt 3\cdot \theta} \]

代入初始条件则有

\[\rho(0)=200\sqrt 3 \\C=200\sqrt 3 \]

飞蛾飞过的路径表示为

\[\begin{align} \text d s&=\sqrt{\left(\rho(\theta)\text d\theta\right )^2+(\text d\rho(\theta))^2}\\ ds&=2\rho(\theta)\text d\theta \\ \int_0^{+\infty}2\rho(\theta)\text d\theta&=400\sqrt 3\cdot\int_0^{+\infty}\text e^{-\sqrt 3\cdot \theta}\text d\theta=400 \end{align} \]

飞行轨迹图

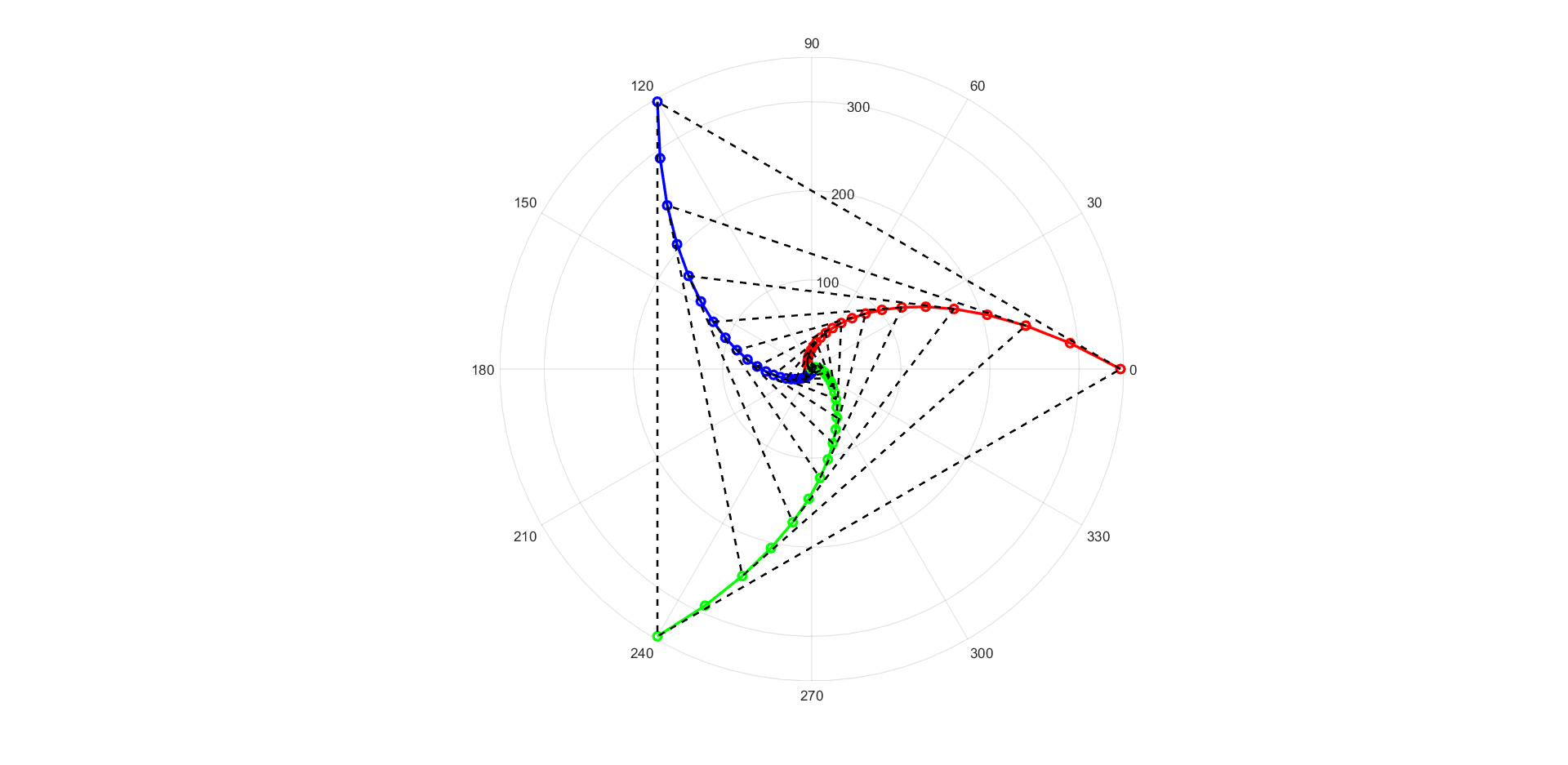
matlab绘图

theta=0:0.1:2*pi;
f_rho=@(theta)200*sqrt(3)*exp(-sqrt(3).*theta);
rho=f_rho(theta);
theta2=theta+2/3*pi;
rho2=f_rho(theta2);
theta3=theta-2/3*pi;
rho3=f_rho(theta3);

figure(1)
polarplot(theta,rho,'r-o','linewidth',2);hold on
polarplot(theta2,rho,'b-o','linewidth',2);
polarplot(theta3,rho,'g-o','linewidth',2);
for i=1:2:length(theta)
    polarplot([theta(i),theta2(i),theta3(i),theta(i)],rho(i)*[1,1,1,1],'k--','linewidth',1.5);hold on
end