C++： 基于四叉树数据结构的自适应网格（初探）

C++： 基于四叉树数据结构的自适应网格

二叉树是一种典型的非线性存储数据结构，查找效率可以达到\(O(log_2N)\)，同样，这类树状结构存在许多种变体，详细参考邓俊辉老师的《数据结构C++》课程。在这里不详细介绍树状数据结构的具体特性，只是初步尝试下基于四叉树数据结构如何实现\(CFD\)计算网格的自适应功能。

四叉树数据数据结构

四叉树数据结构与二维空间网格对应关系如下图所示

基于四叉树数据结构，容易实现对于二维空间区域的局部细化，这对于\(CFD\)计算是十分有用的。一般来说，网格的好坏能够很大程度上影响\(CFD\)数值计算过结果的准确性，网格越精细，流场空间分辨率也就越高，能够描述更为细致的流场，同时也意味着，需要求解的线性方程组更加庞大。

自适应网格就是为了优化此类问题而提出的，在流场内，物理量梯度较大的地方，设置更加细致的网格，流场平缓的区域，网格可以适当稀疏。然而，一般的多面体、多边形网格划分难度较大，为了划分合适的贴体网格，精确拟合物体表面，网格划分过程中计算量同样巨大。因此，自适应网格一般都是基于简单的几何体，规整地四分或者八分网格，以此达到网格划分。著名的\(CFD\)开源求解程序\(Gerris\)，便拥有基于四/八叉树建立的网格自适应功能。

源码项目地址(还没更新)

demo

例子：在一块宽度为\(\pi\)的方形区域中间，定义一条曲线\(z=sin(x+t)\)，在曲线周围设置网格加密最大至7层，曲线上下0.5为加密区域。效果如下

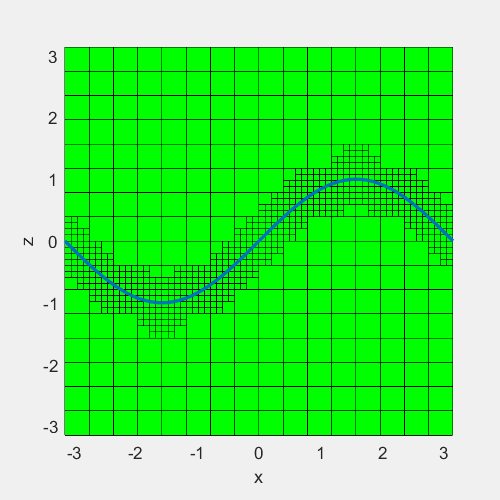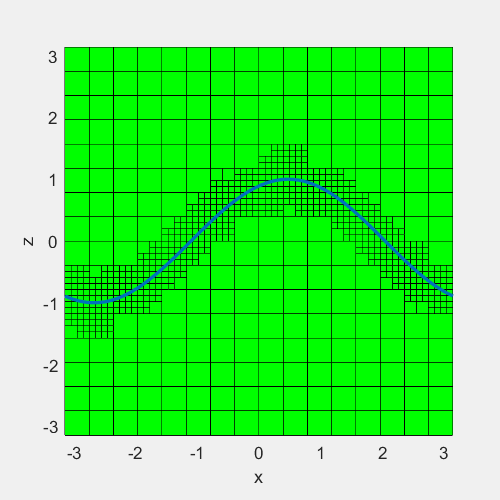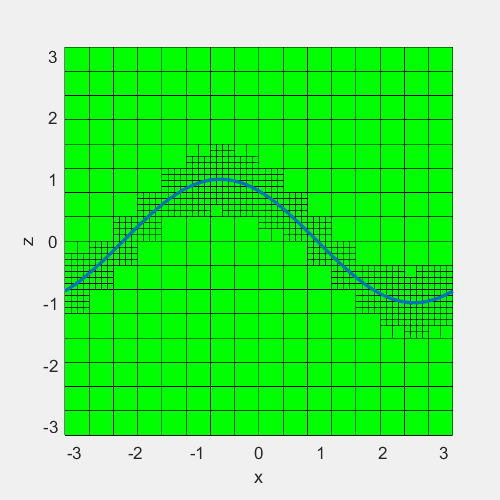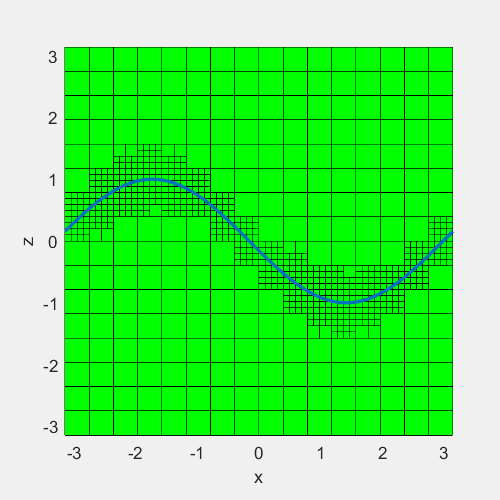
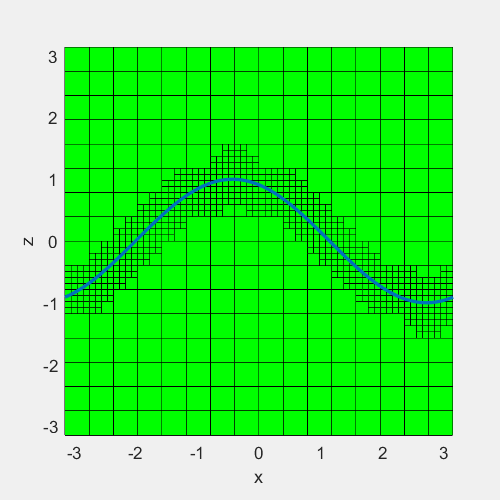
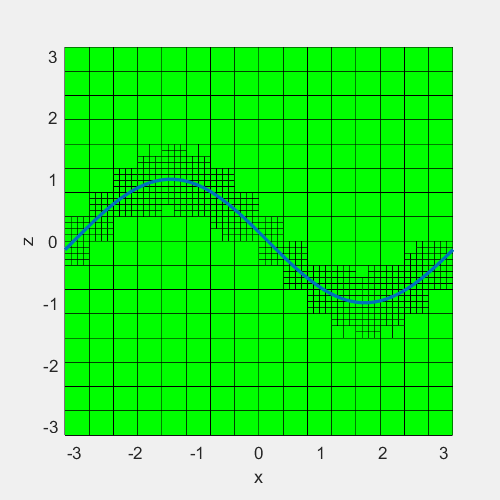
#include <iostream>
#include "QuadTree.h"
#include "PanelTree.h"
using namespace std;
#define PI 3.1415926
double Eta(const Panel& e, double t) {
	double x=e.Centroid(0, 0);
	double y=e.Centroid(1, 0);
	double z = e.Centroid(2, 0);
	return sin(x + t);
}

int main(){
	Panel patch({ -PI,0,-PI }, { -PI,0,PI }, { PI,0,PI }, { PI,0,-PI });
	PanelTree tree(patch);
	char buff[100];
	for (int i = 0; i < 100; i++) {
		sprintf_s(buff, "leafsfile_%04d.txt", i);
        //最大加密至7层，曲线上下0.5为加密区域
		tree.Expand_demo(tree.root, 7, i/30., Eta, 0.5, -0.5);
		tree.WriteLeafsNode(buff);
	}
	return 0;
}

四叉树模板类 ADT

四叉树模板类

/*QuadTree.h
* Include; TreeNode Class, QuadTree Class
*/
#pragma once
#include <iostream>
#include <vector>
#include <iomanip>
#include <fstream>
#define FormatOut(string,X) std::cout<< std::setw(20) << std::left <<string<<":"<< (#X)<<" = "<<X<<std::endl

template<class T> using vector = std::vector<T>;
template<class T> class TreeNode;
template<class T> using TreeNodePosi = TreeNode<T>*;

#define HasChild(p) (p->c1st!=NULL||p->c2nd!=NULL||p->c3rd!=NULL||p->c4th!=NULL)
#define HasParent(p) (p->parent!=NULL)
template<class T>
class TreeNode {
public:
	T element;
	TreeNodePosi<T> parent, c1st, c2nd, c3rd, c4th;
	int height;
	TreeNode() :parent(NULL), c1st(NULL), c2nd(NULL), c3rd(NULL), c4th(NULL), height(1) {}
	TreeNode(T e) : element(e), parent(NULL), c1st(NULL), c2nd(NULL), c3rd(NULL), c4th(NULL), height(1) {}
	TreeNode(T e, TreeNodePosi<T> p) :element(e), parent(p), c1st(NULL), c2nd(NULL), c3rd(NULL), c4th(NULL) {
		this->height = 1 + p->height;
	}
	void insertAsc1st(T const& e) { this->c1st = new TreeNode(e, this); this->c1st->height = this->height + 1; }
	void insertAsc2nd(T const& e) { this->c2nd = new TreeNode(e, this); this->c2nd->height = this->height + 1; }
	void insertAsc3rd(T const& e) { this->c3rd = new TreeNode(e, this); this->c3rd->height = this->height + 1; }
	void insertAsc4th(T const& e) { this->c4th = new TreeNode(e, this); this->c4th->height = this->height + 1; }
};

template<class T>
class QuadTree {
public:
	int Leaf_Num;
	vector<TreeNodePosi<T>> Leafs;
	int size;
	TreeNodePosi<T> root;
	QuadTree() :root(NULL), size(0), Leaf_Num() {}
	QuadTree(const T &root_node) :size(1), Leaf_Num(1) {
		root = new TreeNode<T> (root_node);
	}
	virtual void Expand(TreeNodePosi<T> p);					//Expend 1 Level
	virtual void Expand(TreeNodePosi<T> p, int Level);		//Expand to Level
	void DeleteTreeNode(TreeNodePosi<T>& p) { delete p; p = NULL; 
	}					//delete TreeNode
	void DeleteTree(TreeNodePosi<T>& p);						//delete Tree at p
	~QuadTree() {
		DeleteTree(this->root); 
		delete root; 
		root = NULL;
		std::cout << "QuadTree deconstructor" << std::endl;
	}
	void Travers(TreeNodePosi<T> p, vector<TreeNodePosi<T>>& S);
	void Travers();
	void WriteLeafsNode(const char* filename);
};

template<class T>
void QuadTree<T>::Expand(TreeNodePosi<T> p) {
	T c1_sub, c2_sub, c3_sub, c4_sub;
	p->insertAsc1st(c1_sub);
	p->insertAsc2nd(c2_sub);
	p->insertAsc3rd(c3_sub);
	p->insertAsc4th(c4_sub);
	size += 4;
}

template<class T>
void QuadTree<T>::Expand(TreeNodePosi<T> p, int Level){
	if (p->height >= Level) return;
	else {
		this->Expand(p);
		this->Expand(p->c1st, Level);
		this->Expand(p->c2nd, Level);
		this->Expand(p->c3rd, Level);
		this->Expand(p->c4th, Level);
	}
}

template<class T>
inline void QuadTree<T>::DeleteTree(TreeNodePosi<T>& p){
	if (p == NULL) return;
	if (HasChild(p)) {
		DeleteTree(p->c1st); DeleteTreeNode(p->c1st);
		DeleteTree(p->c2nd); DeleteTreeNode(p->c2nd);
		DeleteTree(p->c3rd); DeleteTreeNode(p->c3rd);
		DeleteTree(p->c4th); DeleteTreeNode(p->c4th);
	}
	else {
		DeleteTreeNode(p);
	}
}

template<class T>
inline void QuadTree<T>::Travers(TreeNodePosi<T> p, vector<TreeNodePosi<T>>& S){
	if (p == NULL) return;
	if (!HasChild(p)) {
		S.push_back(p);
	}
	else {
		Travers(p->c1st, S);
		Travers(p->c2nd, S);
		Travers(p->c3rd, S);
		Travers(p->c4th, S);
	}
}

template<class T>
inline void QuadTree<T>::Travers(){
	Leafs.clear();
	Travers(this->root, this->Leafs);
	Leaf_Num = Leafs.size();
	FormatOut("Leaf Size", Leaf_Num);
}
//output file!!! Note: the class T should overload << operator
template<class T>
void QuadTree<T>::WriteLeafsNode(const char* filename){
	this->Travers();
	std::ofstream fout(filename);
	for (TreeNodePosi<T> p : this->Leafs)
		fout << p->element;
	fout.close();
}

PanelTree 类

PanelTree类继承自QuadTree类，数据成员为自定义的Panel结构体，源码依赖开源矩阵库\(Eigen\)

/*
*PanelTree.h
*/
#pragma once
#include "QuadTree.h"
#include <iostream>
#include <iomanip>
#include <fstream>
#include "Eigen/Dense"

#define FOUT_V(name) out << std::setw(20) << std::scientific << std::setprecision(4) << e.##name<<","


#define FOUT(name) out << std::setw(20) << std::scientific << std::setprecision(4) << e.##name(0, 0)<<","\
					   << std::setw(20) << std::scientific << std::setprecision(4) << e.##name(1, 0)<<","\
					   << std::setw(20) << std::scientific << std::setprecision(4) << e.##name(2, 0)<<","

template<class T> using Mat3 = Eigen::Matrix<T, 3, 1>;

using string = std::string;
using ofstream = std::ofstream;

struct Panel {
public:
	Mat3<double> P1 = { 0,0,0 };
	Mat3<double> P2 = { 0,0,0 };
	Mat3<double> P3 = { 0,0,0 };
	Mat3<double> P4 = { 0,0,0 };
	Mat3<double> Centroid = { 0,0,0 };
	Mat3<double> Normal = { 0,0,0 };
	double ds, Fraction;
	Panel(Mat3<double> p1, Mat3<double> p2, Mat3<double> p3, Mat3<double> p4);
	Panel() {};
	Panel(const Panel& e);                  //copy constructor
	Panel& operator =(const Panel& e);      //overload = 
	void Cal();
	void Cal_Fraction(double eta);
	friend ofstream& operator << (ofstream& out, const Panel& e) {
		FOUT(Centroid); FOUT(Normal);
		FOUT_V(ds); FOUT_V(Fraction);
		FOUT(P1); FOUT(P2); FOUT(P3); FOUT(P4);
		out << std::endl;
		return out;
	}
};

class PanelTree : public QuadTree<Panel>
{
public:
	PanelTree(const Panel &root) :QuadTree<Panel>(root) {}
public:
	bool IsContainFreeSurface(Panel& e, double t, double (*Eta)(const Panel&, double));
	bool IsNearFreeSurface(Panel& e, double t, double (*Eta)(const Panel&, double), double up, double down);
	//bool IsContainCircle(Panel& e, double t, Mat3<double>(*Circle)(const Panel&, double));
	//bool IsNearCircle(Panel& e, double t, Mat3<double>(*Circle)(const Panel&, double), double r0);
	virtual void Expand(TreeNodePosi<Panel> p) override;
	void Expand_demo(TreeNodePosi<Panel> p, int Level, double t, double (*Eta)(const Panel&, double), double up, double down);
};

/*
*PanelTree.cpp
*/
#include "PanelTree.h"

Panel::Panel(Mat3<double> p1, Mat3<double> p2, Mat3<double> p3, Mat3<double> p4) {
	this->P1 = p1; this->P2 = p2; this->P3 = p3; this->P4 = p4;
	this->Cal();//计算中心、ds、法相向量等参数；
	this->Fraction = 0;
}

Panel::Panel(const Panel& e) {
	this->P1 = e.P1;    this->P2 = e.P2;    this->P3 = e.P3;    this->P4 = e.P4;
	this->Centroid = e.Centroid;
	this->Normal = e.Normal;
	this->Fraction = e.Fraction;
	this->ds = e.ds;
}

Panel& Panel::operator =(const Panel& e) {
	this->P1 = e.P1;    this->P2 = e.P2;    this->P3 = e.P3;    this->P4 = e.P4;
	this->Centroid = e.Centroid;
	this->Normal = e.Normal;
	this->Fraction = e.Fraction;
	this->ds = e.ds;
	return *this;
}

void Panel::Cal() {
	Mat3<double> n1 = { 0,0,0 }, n2 = { 0,0,0 };
	double Costheta = 0, Sintheta = 0;
	Mat3<double> tmp = { 0,0,0 };
	n1 = P1 - P3;
	n2 = P2 - P4;
	Costheta = n1.dot(n2) / (n1.norm() * n2.norm());
	Sintheta = sqrt(1 - pow(Costheta, 2));
	ds = 0.5 * (n1.norm() * n2.norm() * Sintheta);
	Centroid = (P1 + P2 + P3 + P4) / 4.;
	tmp = n1.cross(n2);
	Normal = tmp.normalized();
}

void Panel::Cal_Fraction(double eta) {
	double f[4]{};
	f[0] = this->P1(2, 0) - eta;
	f[1] = this->P2(2, 0) - eta;
	f[2] = this->P3(2, 0) - eta;
	f[3] = this->P4(2, 0) - eta;
	double fN = 0, fP = 0;
	if (f[0] <= 0 && f[1] <= 0 && f[2] <= 0 && f[3] <= 0)
		this->Fraction = 1.;
	else {
		if (f[0] >= 0 && f[1] >= 0 && f[2] >= 0 && f[3] >= 0)
			this->Fraction = 0.;
		else {
			for (int i = 0; i < 4; ++i) {
				if (f[i] >= 0) fP += f[i];
				else fN += f[i];
			}
			this->Fraction = abs(fN) / (abs(fP) + abs(fN));
		}
	}
}


bool PanelTree::IsContainFreeSurface(Panel& e,double t,double(*Eta)(const Panel&, double)){
	double eta = Eta(e, t);
	e.Cal_Fraction(eta);
	return !((abs(e.Fraction - 1) < 1.0e-5) || (abs(e.Fraction - 0) < 1.0e-5));
}

bool PanelTree::IsNearFreeSurface(Panel& e, double t, double(*Eta)(const Panel&, double), double up, double down){
	double eta = Eta(e, t);
	e.Cal_Fraction(eta);
	double z = e.Centroid(2, 0);
	return ((z - eta) >= down && (z - eta) <= up);
}

//bool PanelTree::IsContainCircle(Panel& e, double t, Mat3<double>(*Circle)(const Panel&, double))
//{
//	return false;
//}
//
//bool PanelTree::IsNearCircle(Panel& e, double t, Mat3<double> (*Circle)(const Panel&, double), double r0)
//{
//	Mat3<double> pos = Circle(e, t);
//	double dis = (e.Centroid - pos).norm();
//	return abs(dis)<=r0;
//}

void PanelTree::Expand(TreeNodePosi<Panel> p){
	Panel subP1, subP2, subP3, subP4;
	Mat3<double> c12 = { 0,0,0 };
	Mat3<double> c23 = { 0,0,0 };
	Mat3<double> c34 = { 0,0,0 };
	Mat3<double> c41 = { 0,0,0 };
	c12 = (p->element.P1 + p->element.P2) / 2.;
	c23 = (p->element.P2 + p->element.P3) / 2.;
	c34 = (p->element.P3 + p->element.P4) / 2.;
	c41 = (p->element.P4 + p->element.P1) / 2.;
	//subP1
	subP1.P1 = p->element.P1;
	subP1.P2 = c12;
	subP1.P3 = p->element.Centroid;
	subP1.P4 = c41;
	//subP2
	subP2.P1 = p->element.P2;
	subP2.P2 = c23;
	subP2.P3 = p->element.Centroid;
	subP2.P4 = c12;
	//subP3
	subP3.P1 = p->element.P3;
	subP3.P2 = c34;
	subP3.P3 = p->element.Centroid;
	subP3.P4 = c23;
	//subP4
	subP4.P1 = p->element.P4;
	subP4.P2 = c41;
	subP4.P3 = p->element.Centroid;
	subP4.P4 = c34;
	subP1.Cal();	subP2.Cal();	subP3.Cal();	subP4.Cal();
	p->insertAsc1st(subP1); p->insertAsc2nd(subP2);
	p->insertAsc3rd(subP3); p->insertAsc4th(subP4);
	Leaf_Num += 3;
	size += 4;
}

void PanelTree::Expand_demo(TreeNodePosi<Panel> p, int Level, double t, double (*Eta)(const Panel&, double), double up, double down)
{
	if (p->height >= Level) return;
	bool IsMin = p->height <= 4;
	bool IsContain = this->IsContainFreeSurface(p->element, t, Eta);
	bool IsNear = this->IsNearFreeSurface(p->element, t, Eta, up, down);
	if (IsMin||IsNear||IsContain) {
		this->Expand(p);
		this->Expand_demo(p->c1st, Level, t, Eta, up, down);
		this->Expand_demo(p->c2nd, Level, t, Eta, up, down);
		this->Expand_demo(p->c3rd, Level, t, Eta, up, down);
		this->Expand_demo(p->c4th, Level, t, Eta, up, down);
	}
}