数值计算:粒子群优化算法(PSO)
PSO
最近需要用上一点最优化相关的理论,特地去查了些PSO算法相关资料,在此记录下学习笔记,附上程序代码。基础知识参考知乎大佬文章,写得很棒!
传送门
背景
起源:1995年,受到鸟群觅食行为的规律性启发,James Kennedy和Russell Eberhart建立了一个简化算法模型,经过多年改进最终形成了粒子群优化算法(Particle Swarm Optimization, PSO) ,也可称为粒子群算法[1] 。
特点:粒子群算法具有收敛速度快、参数少、算法简单易实现的优点(对高维度优化问题,比遗传算法更快收敛于最优解)。
基本思想:粒子群算法的思想源于对鸟群觅食行为的研究,鸟群通过集体的信息共享使群体找到最优的目的地。
算法原理
| 鸟群觅食 | 粒子群算法 |
|---|---|
| 鸟 | 粒子 |
| 森林 | 求解空间 |
| 食物的量 | 目标函数值 |
| 每只鸟所处的位置 | 空间中的一个解(粒子位置) |
| 食物量最多的位置 | 全局最优解 |
-
每个粒子包含两个属性
- 速度:下一时刻粒子移动的方向与距离。
- 位置:所求问题粒子的当前解。
-
算法的6个重要参数
在\(D\)维空间中,有\(n\)个粒子。
-
第\(i(i=1,2,\cdots,n)\)个粒子的位置
\[\begin{align} X_{i}=\left [ x_{i1},x_{i2},\cdots,x_{iD}\right ] \end{align} \] -
第\(i(i=1,2,\cdots,n)\)个粒子的速度(粒子移动方向和大小)
\[\begin{align} V_{i}=\left [ v_{i1},v_{i2},\cdots,v_{iD}\right ] \end{align} \] -
第\(i(i=1,2,\cdots,n)\)个粒子的搜索到的最优位置(个体最优解)
\[\begin{align} P^{pbest}_{i}=\left [ p_{i1},p_{i2},\cdots,p_{iD}\right ] \end{align} \] -
群体搜索到的最优位置(群体最优解)为
\[\begin{align} P^{gbest}=\left [ p^{gbest}_{1},p^{gbest}_{2},\cdots,p^{gbest}_{D}\right ] \end{align} \] -
第 \(i(i=1,2,\cdots,n)\) 个粒子搜索到的最优位置的适应值(优化目标函数的值)为
\[\begin{align} f^p_i:\text{粒子历史最优适应值} \end{align} \] -
群体搜索到的最优位置的适应值为
\[\begin{align} f^g:\text{群体历史最优适应值} \end{align} \]
-
-
算法流程图
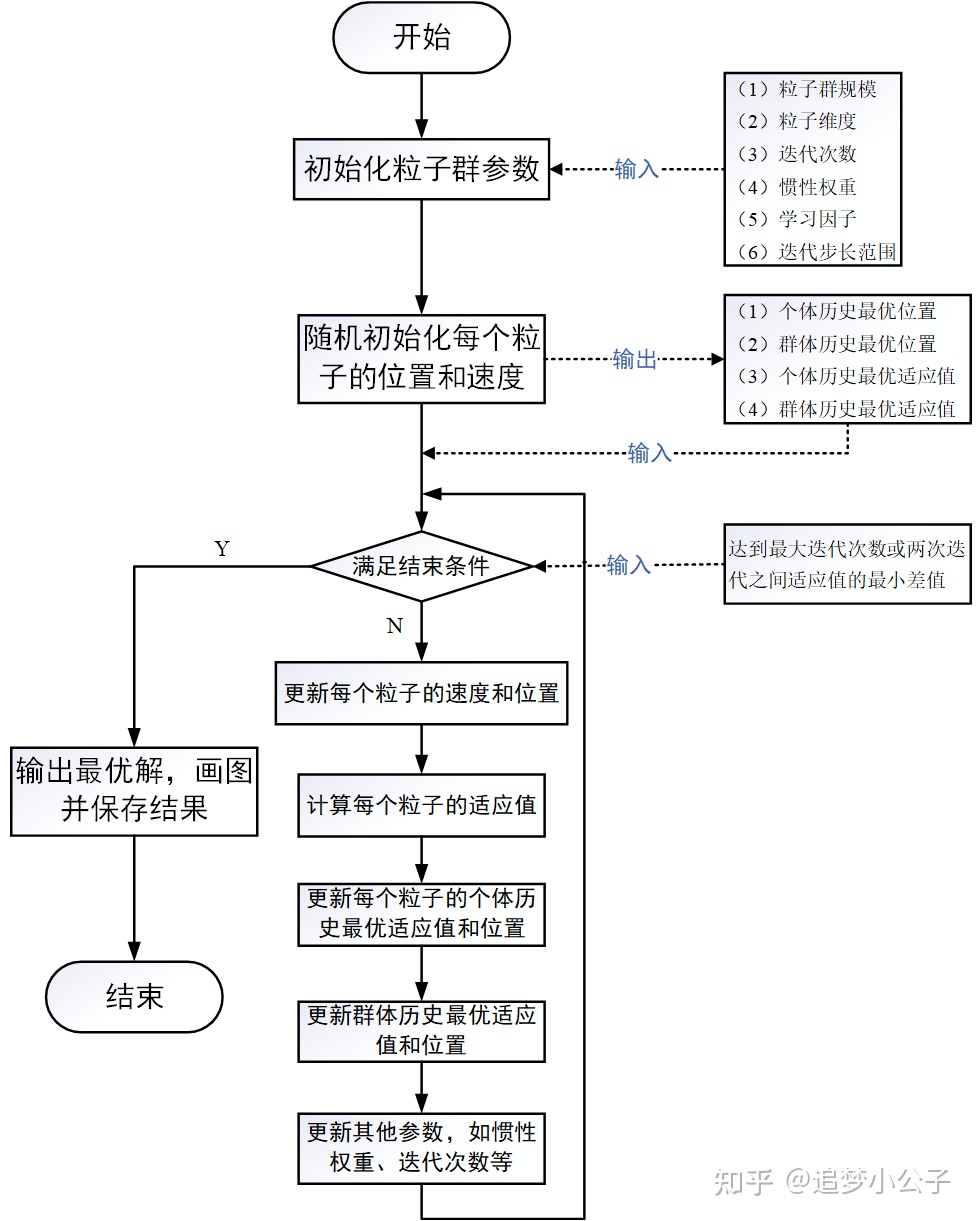
-
速度更新公式
\[\begin{align} V^{k+1}_{i}=\omega \cdot V^{k}_{i}+c_1r_1(P^{pbest}_{i}-X^{k}_{i})+c_2r_2(P^{gbest}_{i}-X^{k}_{i}) \end{align} \]\(r_1,r_2\)为区间\([0,1]\)内的随机数,\(\omega\)为权重因子,\(c_1,c_2\)分别为个体、群体学习因子
-
第一项:惯性部分
由惯性权重和粒子自身速度构成,表示粒子对先前自身运动状态的信任。
-
第二项:认知部分
表示粒子本身的思考,即粒子自己经验的部分,可理解为粒子当前位置与自身历史最优位置之间的距离和方向。
-
第三项:社会部分
表示粒子之间的信息共享与合作,即来源于群体中其他优秀粒子的经验,可理解为粒子当前位置与群体历史最优位置之间的距离和方向
\[\text{更新速度方向}=\text{惯性方向 + 个体最优方向 + 群体最优方向} \] -
-
位置更新公式
\[\begin{align} X^{k+1}_{i}=X^{k}_{i}+V^{k}_{i} \end{align} \]
算法的参数解释
-
粒子群规模\(n\)
一个正整数,推荐取值范围:[20,1000],简单问题一般取20~40,较难或特定类别的问题可以取100~200。较小的种群规模容易陷入局部最优;较大的种群规模可以提高收敛性,更快找到全局最优解,但是相应地每次迭代的计算量也会增大;当种群规模增大至一定水平时,再增大将不再有显著的作用。
-
粒子维度\(D\)
粒子搜索的空间维数即为自变量的个数。
-
迭代次数\(K\)
推荐取值范围:[50,100],典型取值:60、70、100
-
惯性权重\(\omega\)
惯性权重\(\omega\)描述粒子上一代速度对当前代速度的影响。\(\omega\)值较大,全局寻优能力强,局部寻优能力弱;反之,则局部寻优能力强。当问题空间较大时,为了在搜索速度和搜索精度之间达到平衡,通常做法是使算法在前期有较高的全局搜索能力以得到合适的种子,而在后期有较高的局部搜索能力以提高收敛精度。所以\(\omega\)不宜为一个固定的常数。
当\(\omega=1\) 时,退化成基本粒子群算法,当 \(\omega=0\) 时,失去对粒子本身经验的思考。推荐取值范围:$$[0.4,2]$$,典型取值:0.9、1.2、1.5、1.8
在解决实际优化问题时,往往希望先采用全局搜索,使搜索空间快速收敛于某一区域,然后采用局部精细搜索以获得高精度的解。线性变化策略:随着迭代次数的增加,惯性权重\(\omega\)不断减小,从而使得粒子群算法在初期具有较强的全局收敛能力,在后期具有较强的局部收敛能力。
\[\omega= \omega_{max}-(\omega_{max}-\omega_{min})\frac{k}{k_{max}} \]\(\omega_{max},\omega_{min}\)为最大,最小惯性权重值,\(k,k_{max}\)为当前迭代次数与最大迭代次数。
-
学习因子\(c_1,c_2\)
也称为加速系数或加速因子(这两个称呼更加形象地表达了这两个系数的作用)
\(c_1=0\):无私型粒子群算法,“只有社会,没有自我”,迅速丧失群体多样性,易陷入局部最优而无法跳出。
\(c_2=0\):自我认知型粒子群算法,“只有自我,没有社会”,完全没有信息的社会共享,导致算法收敛速度缓慢 。
\(c_1,c_2\)都不为0,称为完全型粒子群算法,更容易保持收敛速度和搜索效果的均衡,是较好的选择。 推荐取值范围:[0,4];
典型取值:\(c_1=c_2=2、c_1=1.6,c_2=1.8、c_1=1.6,c_2=2\)针对不同的问题有不同的取值,一般通过试凑来调整这两个值。
粒子群算法条件限制
位置限制
限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
速度限制
为了平衡算法探索能力与开发能力,需要设定一个合理的速度范围,限制粒子的最大速度。
\(V_m\)较大时,粒子飞行速度快,探索能力强,但粒子容易飞过最优解
\(V_m\)较小时,飞行速度慢,开发能力强,但是收敛速度慢,且容易陷入局部最优解
\(V_m\)一般设为每维变量变化范围的10%~20%
优化停止准则
一般有两种:
-
最大迭代步数
-
可接受的满意解:上一次迭代后最优解的适应值与本次迭代后最优解的适应值之差小于某个值后停止优化
初始化:
如果粒子的初始化范围选择得好的话可以缩短优化的收敛时间,我们需要根据具体的问题进行分析。如果根据我们的经验判断出最优解一定在某个范围内,则就在这个范围内初始化粒子;如果无法确定,则以粒子的取值边界作为初始化范围。
MATLAB编程实现
实例效果
采用面相对象的编程思路,将完整的\(PSO\)算法以及数据成员封装到类中,\(demo.m\)实例以及\(PSO.m\)类代码见后续
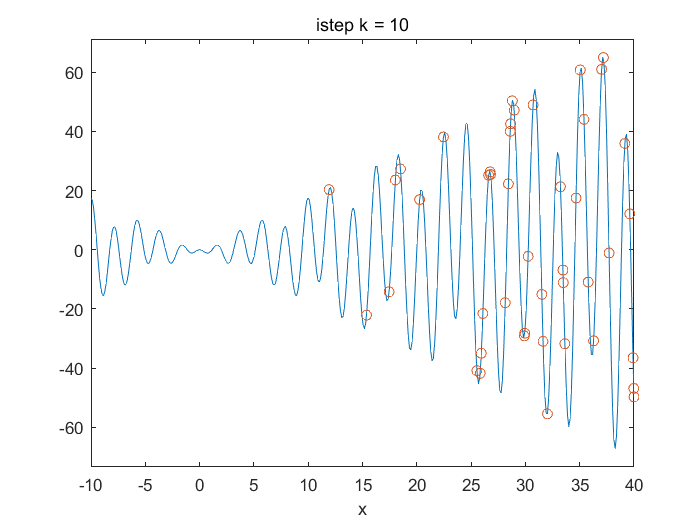
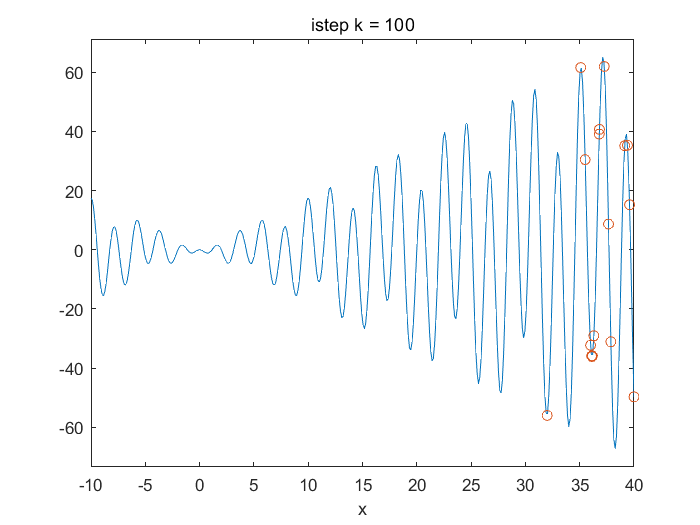
\(Demo1D.m\)以一维函数\(f(x)=xsin(x) \cdot cos(2x)-2xsin(x)\)求\([0,20]\)范围内最小值的PSO算法实例,迭代80时,结果达到收敛。
算法特性
- 支持多维空间变量
- 支持设定位置与速度许可范围(for each dimension)
- 支持常系数与线性压缩权重参数
对于多优化目标还需进一步改进。
\(demo1D.m\)
clc;clear all;
f= @(x)(x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x)); % 函数表达式
pso=PSO(f,50,1);
pso.SetRangeLim([-10,40],[-4,4]); %设置位置与速度范围
%pso.SetOmega("const",0.2);
pso.SetOmega("linear",[0.5,2]); %设置权重Omega因子
pso.solve(200); %迭代求解100步
%% Plot
figure(111)
for i=1:1:pso.k_max
ezplot(f,[-10,0.01,40]);
hold on
x=pso.record_X_V{i,1}(:,1);
plot(x,f(x),'o'); title(num2str(i,"istep k = %d"))
hold off
pause(0.1)
end

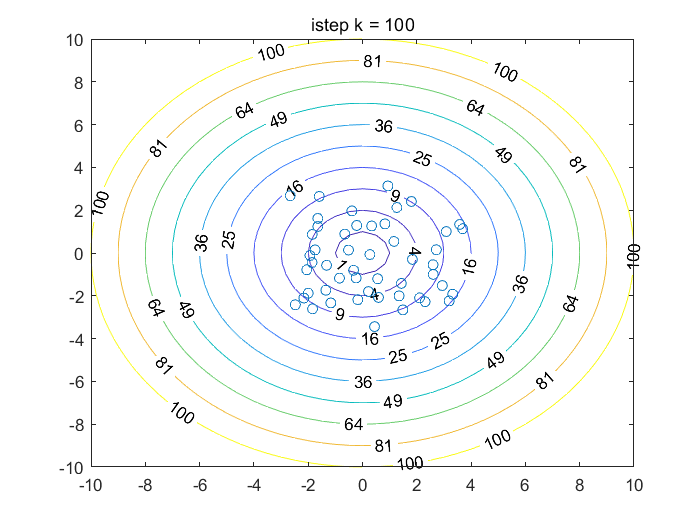
\(demo2D.m\)
clc;clear all;
%%
f= @(x)x(:,1).^2+x(:,2).^2;
pso=PSO(f,50,2);
pso.SetRangeLim([-10,-10;10,10],[-2,-2;2,2]); %设置位置与速度范围
pso.SetOmega("linear",[0.4,2]); %设置权重Omega因子
pso.Set_C_factor(1,1); %设置学习因子
pso.solve(200); %迭代求解100步
%% plot
figure(112)
[X,Y] = meshgrid(-10:0.5:10,-10:0.5:10);
Z=X.^2+Y.^2;
line=[0:1:10].^2;
%for i=1:1:pso.k_max
for i=160
contour(X,Y,Z,line,'ShowText','on');
hold on
x=pso.record_X_V{i,1}(:,1);
y=pso.record_X_V{i,1}(:,2);
plot(x,y,'o'); title(num2str(i,"istep k = %d"))
hold off
pause(0.1)
end


\(PSO.m \quad class\)
classdef PSO < handle
%PSO 算法类
properties
%% 目标函数
func;
%%
N=50; %种群个数,默认值50
D=1; %变量空间维数
k_max=100;%最大迭代步数,默认值为100
%%
omega; %权重因子/范围
flag_omega="const";%权重形式
c1=1; %个体学习因子
c2=1; %群体学习因子
%% 粒子属性
X; %位置
V; %速度
flag_lim=false;
lim_X; %位置限制范围
lim_V; %速度限制范围
%% 记录
X_pbest; %粒子个体最佳位置
X_gbest; %粒子群体最佳位置
func_pbest; %每个个体的历史最佳适应度
func_gbest; %种群历史最佳适应度
%%
k; %当前迭代步
%%
record_func; %记录位置与速度
record_X_V;
flag_plot=false;
end
methods
function self = PSO(func,N,D)
%PSO 构造函数
% fun:目标函数
% N :粒子数目
% D :空间维数
self.func=func;
self.N=N;
self.D=D;
self.X=zeros(self.N,self.D);
self.V=zeros(self.N,self.D);
self.X_pbest=zeros(self.N,self.D);
self.X_gbest=zeros(1,self.D);
self.func_pbest=ones(self.N,1)*1.0e10;
self.func_gbest=1.0e10;
fprintf("创建PSO Model完成\n");
end
function solve(self,k_max)
%求解
self.k=1;
self.record_func=zeros(k_max,self.D+1);%初始化记录容器
self.record_X_V=cell(k_max,1);
self.k_max=k_max;
self.Initial(); %初始化
while(self.k<=self.k_max)
self.Update_p_g_best(); %更新群体
self.Update_V_X(); %更新速度、位置
self.k=self.k+1;
self.Report(10);
end
end
function SetRangeLim(self,limX,limV)
%设置空间位置与速度限制范围
% limX(1,i):第i维数据最小值
% limX(2,i):第i维数据最大值
self.flag_lim=true;
self.lim_X=ones(2,self.D);
self.lim_X(1,:)=limX(1,:);
self.lim_X(2,:)=limX(2,:);
self.lim_V=ones(2,self.D);
self.lim_V(1,:)=limV(1,:);
self.lim_V(2,:)=limV(2,:);
end
function Set_C_factor(self,c1,c2)
%设置学习因子
% c1:个体学习因子
% c2:群体学习因子
self.c1=c1;
self.c2=c2;
end
function Initial(self)
%初始化粒子位置
if self.flag_lim
for d=1:1:self.D
for i=1:1:self.N
self.X(i,:)=self.lim_X(1,d)+(self.lim_X(2,d)-self.lim_X(1,d))*...
rand(1,self.D);
self.V(i,:)=self.lim_V(1,d)+(self.lim_V(2,d)-self.lim_V(1,d))*...
rand(1,self.D);
end
end
else
for i=1:1:self.N
self.X(i,:)= rand(1,self.D);
self.V(i,:)= rand(1,self.D);
end
end
fprintf("PSO Model初始化完成\n");
end
function SetOmega(self,flag,omega)
self.flag_omega=flag;
self.omega=omega;
end
function Update_V_X(self)
%更新速度矢量,与当前位置
% flag == const 常系数权重 omega为常值
% flag == linear 线性权重 omega为范围
if self.flag_omega == "const"
omega_=self.omega;
elseif self.flag_omega == "linear"
omega_=self.omega(2)-(self.omega(2)-self.omega(1))*(self.k/self.k_max);
end
for i=1:1:self.N
self.V(i,:)=self.V(i,:)*omega_+...
self.c1*bsxfun(@times,self.X_pbest(i,:)-self.X(i,:),rand(1,self.D))+...
self.c2*bsxfun(@times,self.X_gbest-self.X(i,:),rand(1,self.D));
end
if self.flag_lim
% 限制速度范围
for i=1:1:self.D
tmpV=self.V(:,i);
tmpV(tmpV<self.lim_V(1,i))=self.lim_V(1,i);
tmpV(tmpV>self.lim_V(2,i))=self.lim_V(2,i);
self.V(:,i)=tmpV;
end
end
self.X=self.X+self.V; %g更新位置
if self.flag_lim
% 限制位置范围
for i=1:1:self.D
tmpX=self.X(:,i);
tmpX(tmpX<self.lim_X(1,i))=self.lim_X(1,i);
tmpX(tmpX>self.lim_X(2,i))=self.lim_X(2,i);
self.X(:,i)=tmpX;
end
end
self.record_X_V{self.k,1}=[self.X,self.V];
end
function Update_p_g_best(self)
% 更新X_pbest,X_gbest
func_x=self.func(self.X); % 个体当前适应度(函数值)
for i=1:1:self.N
if self.func_pbest(i) > func_x(i)
self.func_pbest(i)=func_x(i);
self.X_pbest(i,:)=self.X(i,:);
end
end
if self.func_gbest > min(self.func_pbest)
[self.func_gbest, nmin] = min(self.func_pbest); % 更新群体历史最佳适应度
self.X_gbest = self.X_pbest(nmin, :); % 更新群体历史最佳位置
end
self.record_func(self.k,:)=[self.X_gbest,self.func_gbest];
end
function Report(self,step)
if(mod(self.k,step)==0)
fprintf("\nCurrent istep k = %d\n",self.k);
fprintf("X = %f func= %f\n",self.X_gbest,self.func_gbest);
fprintf("Residual(func) = %f \n",abs(self.record_func(self.k-1,2)-self.record_func(self.k-2,2)));
end
end
end
end
参考文献
[1] Kennedy J . Particle swarm optimization[J]. Proc. of 1995 IEEE Int. Conf. Neural Networks, (Perth, Australia), Nov. 27-Dec. 2011, 4(8):1942-1948 vol.4.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号