异常值检验（1）
Outlier Detection
Generalized ESD Test
数据集：\(\left\{ x_{1}, x_{2}, \ldots, x_{n} \right\}\)
原假设 \(H_{0}\)：数据集中不存在异常值。
备择假设 \(H_{1}:\) 最多存在 \(r\) 个异常值。
计算统计量：
其中，\(\bar{x}\) 为样本均值，\(s\) 为样本标准差。
移除使得 \(x_{i} - \bar{x}\) 最大的 \(x_{i}\)，在剩余的 \((n - 1)\) 个 sample 上重新计算 \(R_{i}\)。重复此过程，得到 \(R_{1}, R_{2}, \ldots, R_{r}\)。
令显著性水平为 \(\alpha\)，对于 \(i = 1, 2, \ldots, r\)，分别计算：
以上，\(t_{p, v}\) 是自由度为 \(v\) 的 t-distribution 的 \(100p\) 分位点，其中：
根据 Rosner 的数据模拟，该假设检验方法在样本量 \(n \geq 25\) 时非常精确，在 \(n \geq 15\) 时较为精确。
代码实现如下：
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as stats
y = np.random.random(100)
x = np.arange(len(y))
plt.scatter(x, y)
plt.show()
y[14] = 9
y[83] = 10
y[44] = 14
plt.scatter(x, y)
plt.show()
def test_stat(y, iteration):
stdev = np.std(y)
avg_y = np.mean(y)
abs_val_minus_avg = abs(y - avg_y)
max_of_deviations = max(abs_val_minus_avg)
max_ind = np.argmax(abs_val_minus_avg)
cal = max_of_deviations / stdev
print(f'Test Statistics Value(R{iteration}) : {cal}')
return cal, max_ind
def calc_critical(size, alpha, iteration):
t_dist = stats.t.ppf(1 - alpha / (2 * size), size - 2)
numerator = (size - 1) * np.sqrt(np.square(t_dist))
denominator = np.sqrt(size) * np.sqrt(size - 2 + np.square(t_dist))
critical = numerator / denominator
print(f'Critical Value(lambda{iteration}) : {critical}')
return critical
def check_values(R, C, inp, max_index, iteration):
if R > C:
print('{} is an outlier. R{} > λ{}: {:.4f} > {:.4f} \n'.format(inp[max_index],iteration, iteration, R, C))
else:
print('{} is not an outlier. R{}> λ{}: {:.4f} > {:.4f} \n'.format(inp[max_index],iteration, iteration, R, C))
def ESD_Test(input_series, alpha, max_outliers):
stats = []
critical_vals = []
for iterations in range(1, max_outliers + 1):
stat, max_index = test_stat(input_series, iterations)
critical = calc_critical(len(input_series), alpha, iterations)
check_values(stat, critical, input_series, max_index, iterations)
input_series = np.delete(input_series, max_index)
critical_vals.append(critical)
stats.append(stat)
if stat > critical:
max_i = iterations
print('H0: there are no outliers in the data')
print('Ha: there are up to 10 outliers in the data')
print('')
print('Significance level: α = {}'.format(alpha))
print('Critical region: Reject H0 if Ri > critical value')
print('Ri: Test statistic')
print('λi: Critical Value')
print('')
df = pd.DataFrame({'i' :range(1, max_outliers + 1), 'Ri': stats, 'λi': critical_vals})
def highlight_max(x):
if x.i == max_i:
return ['background-color: yellow']*3
else:
return ['background-color: white']*3
df.index = df.index + 1
print('Number of outliers {}'.format(max_i))
return df.style.apply(highlight_max, axis = 1)
ESD_Test(y, 0.05, 7)
Mining Distance-based outliers in near linear time with randomization and a Simple pruning rule
给定特征空间上的一个距离测度，存在多种不同基于距离的异常值定义，其中三个经典定义为：
-
异常值为那些使得满足相互距离小于 \(d\) 的其余数据点的个数少于 \(p\) 的数据点。
-
异常值为那些距离它们最近的第 \(k\) 个邻居的距离最大的 \(n\) 个数据点。
-
异常值为那些距离它们最近的 \(k\) 个邻居的平均距离最大的 \(n\) 个数据点。
以上三种定义均存在一定的问题。第一种定义没有把 “距离的排序” 纳入考量，且参数 \(d\) 的值需要进行估计。第二种定义只考虑到 “最近的第 \(k\) 个邻居“，而忽略了前 \(k-1\) 个更近的邻居所包含的信息。第三中定义虽然求的是最近的 \(k\) 个邻居的平均距离，但是时间复杂度却上升了。
算法如下：
代码实现如下：
import numpy as np
import matplotlib.pyplot as plt
# Distance between two points x and y using Euclidean metric.
def distance(x, y):
return np.sqrt(np.sum((y - x) ** 2))
# Return the maximum distance between point x and a point in Y.
def max_dist(x, Y):
return max(map(lambda y: distance(x, y), Y))
# Return the k closest examples in Y to x.
def closest(x, Y, k):
result = []
for y in list(Y):
result.append((y, distance(x, y)))
result.sort(key=lambda tup: tup[1], reverse=True)
return set(map(lambda tup: tup[0], result[:min(k, len(result))]))
# D, a set of examples in random order; k, the number of nearest
# neighbors; n, the number of outliers to return.
def find_outliers(D, k, n):
def score(N, b):
result = list(map(lambda n: distance(b, n), list(N)))
result.sort(reverse=True)
return np.mean(result[:k])
c = 0
O = set()
block_size = len(D) // 5
pointer = 0
while pointer <= len(D):
B = D[pointer: min(pointer+block_size, len(D))]
pointer += block_size
neighbors = dict.fromkeys(B)
for i in neighbors.keys():
neighbors[i] = set()
for d in D:
for b in B:
if b == d:
continue
if len(neighbors[b]) < k or distance(b, d) < max_dist(b, neighbors[b]):
neighbors[b] = closest(b, neighbors[b] | {d}, k)
if score(neighbors[b], b) < c:
B = list(set(B) - {d})
O = set(sorted(list(set(B) | O), reverse=True)[:n])
c = min([score(O, o) for o in list(O)])
return O
y = np.random.random(100)
x = np.arange(len(y))
plt.scatter(x, y)
plt.show()
y[14] = 9
y[83] = 10
y[44] = 14
plt.scatter(x, y)
plt.show()
find_outliers(list(y), 3, 3)
Local Outlier Factor (LOF)
异常值识别通常有两种思路，即基于距离的方法（distance-based approaches）和基于密度的方法（density-based approaches）。前者基于的思想是，观测到一个距离数据分布中心非常远的数据点的概率是极小的，因此这种点可以被视作为一个异常（Mehrotra, 1997）。然而，基于密度的方法也是很重要的，考虑以下情形：
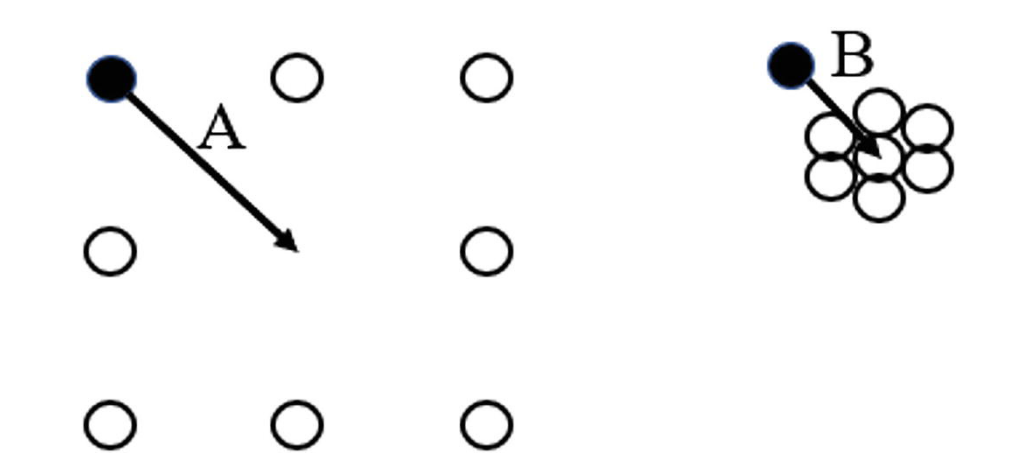
在上方两图中，向量 \(A, B\) 分别指向各自数据集的中心，并且如果以距离的视角看待此问题，向量 \(A\) 的模显然大于向量 \(B\) 的模。然而，相比于向量 \(B\)，相关于向量 \(A\) 的数据点显然更加均匀地排布在其周围，或者简而言之，向量 \(B\) 的坐标显然更像是一个异常值。
在基于密度的识别异常值方法中，我们纳入 “邻域”（neighborhood）的概念，其中一种定义方法是，对于任意一个数据点，给定一个数字 \(n\)，求出数据集中距离它最近的 \(k\) 个点作为它的邻域。KNN（k-nearest neighbors）算法就是对邻域思想的一种实现，由于算法比较基础这里按下不表。KNN 算法与这里提到的基于密度的异常值检验法的区别是，对于 KNN 算法，在确定一个数据点的邻域后算法将停止；然而，对于基于密度的异常值检验方法，在确定一个数据点的邻域后，我们将比较这个数据点的密度与它邻域中所有数据点的密度。如果相比之下，这个点的密度显著低于邻域中其它点的密度，那么这个点更可能是一个异常值。
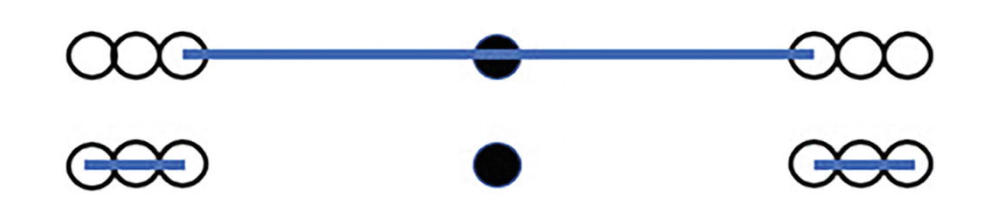
如上图，假设对于任意一个数据点，我们取距离它最近的两个点作为其邻域（即 \(k=2\)）。那么对于黑点，其邻域为两侧靠中间的两个白点，上方的长蓝色线段为邻域覆盖的范围；而对于这两个白点，它们的邻域却分别是外侧的另外两个白点，下方的两段短蓝色线段分别为它们邻域覆盖的范围。显然，黑点的密度远远大于其邻域两个白点的密度，从图中恰好体现出，黑点是一个异常值。
Definition. (Reachability Distance)
Reachability Distance 是一个基于密度和邻域的算法，在计算它之前首先要确定一个邻域的范围。如下例，假设 \(k=5\)：
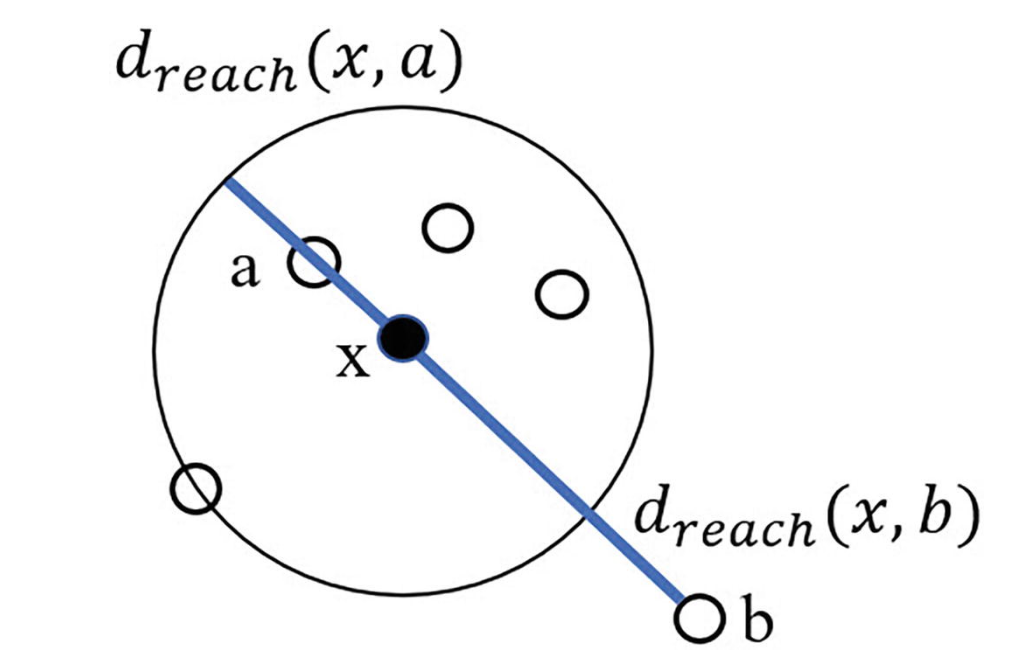
对于数据点 \(x\)，邻域范围 \(k=5\)，我们可以确定数据集中距离 \(x\) 最近的五个点（在图中即为黑点 \(x\) 与除 \(b\) 之外的所有白点，这里的假设是 \(x\) 也可以作为它自身的邻近点）。注意到，点 \(b\) 不在 \(x\) 的邻域中。
我们按照以下方式定义 Reachability Distance：
- 对于在 \(x\) 邻域之外的点 \(p\)，Reachability Distance 为 \(x\) 与 \(p\) 之间的实际距离。
- 对于在 \(x\) 邻域之内的点 \(p\)，Reachability Distance 为 \(x\) 与 数据集中距离 \(x\) 第 \(k\) 近的点之间的距离。
在上图中，圆上的白点为距离 \(x\) 第五近的点（包括 \(x\) 自身），设这个点为 \(o\)，那么对于圆内任意一点，定义点 \(x\) 到它的 Reachability Distance 皆为圆的半径，即 \(d(x, o)\)。而对于圆外任意一点，例如点 \(b\)，点 \(x\) 到点 \(b\) 的 Reachability Distance 即为它们的实际距离 \(d(x, b)\)。
换言之，对于目标点 \(x\)，设数据集中距离 \(x\) 第 \(k\) 近的点为 \(o\)，设它到数据集中另外一点 \(p\) 的 Reachability Distance 为 \(d_{reach}(x, p)\)，那么 \(d_{reach}(x, p)\) 的数学表达式为：
Definition. (Average Reachability Distance)
对于目标点 \(x\)，它的 Average Reachability Distance 定义为 \(x\) 到数据集中除 \(x\) 外所有数据点的平均 Reachability Distances。即，假设数据集为 \(D\)，且 \(|D| = N\)，那么 Average Reachability Distance 定义为：
对于目标点 \(x\)，它的 Average Reachability Distance 衡量了我们为了寻找 \(x\) 的相似点所需要移动的平均距离。
Definition. (Local Average Reachability Distance)
相似地，对于目标点 \(x\)，假设它的邻域为 \(S_{x}\)，且 \(|S_{x}| = k\)，那么它的 Local Average Reachability Distance 定义为：
Definition. (Reachability Density)
对于目标点 \(x\)，它的 Reachability Density 定义为它的 Average Reachability Distance 的倒数，即：
若目标点 \(x\) 的 Average Reachability Distance 越大，说明我们为了寻找与 \(x\) 相似的点所需要移动的平均距离越大，则 \(x\) 的 Reachability Density 越小。
Definition. (Local Reachability Density)
相似地，对于目标点 \(x\)，它的 Local Reachability Density 定义为它的 Local Average Reachability Distance 的倒数，即：
Definition. (Local Outlier Factor)
对于目标点 \(x\)，它的 Local Outlier Factor 定义为：数据集 \(D\) 中除 \(x\) 以外的所有数据点的平均 Local Reachability Density 与 点 \(x\) 的 Local Reachability Density 的比值，即：
Connectivity-Based Outlier Factor
上文介绍的 Local Outlier Factor 的确存在一些实践中的缺陷，最大的缺陷是，异常值并不一定存在于 “低密度” 区域，如下图：
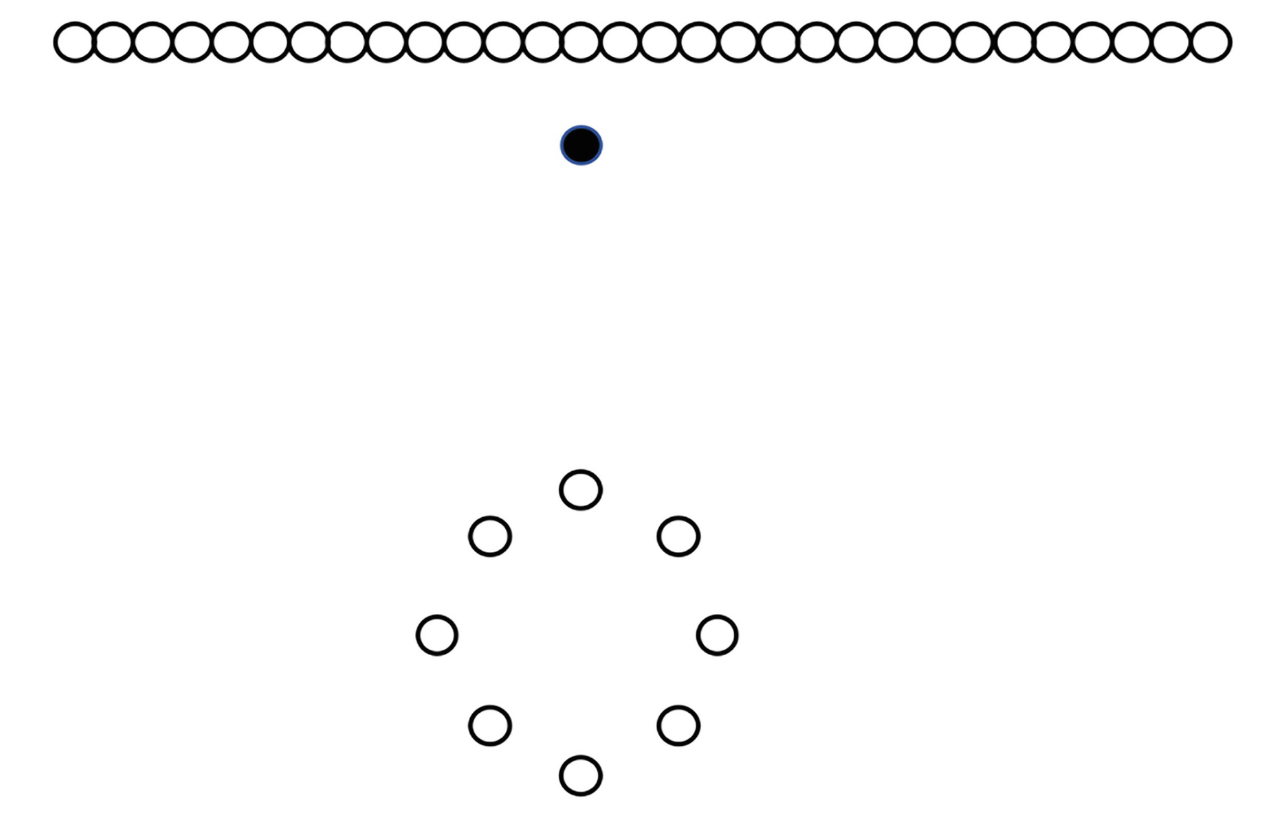
此处，显然上方与下方的白点分别构成两簇，黑点即为异常值。然而，如果我们应用 LOF 算法且将黑点判别为一个异常点，那么下方的白色簇将全部归为异常点，因为该簇中点与点的距离相对较大。
Connectivity-Based Outlier Factor (COF) 是另一种基于密度的聚类方法，并且能够解决上述 LOF 存在的问题。它向 density 中添加了 isolativity 的概念，即，一个点与其它点的联系程度。在上图中，下方构成圆形的白色点彼此之间相互连接，而黑色点却并不属于任何已存在的规律模式（直线或圆），因此，黑点是一个异常值。
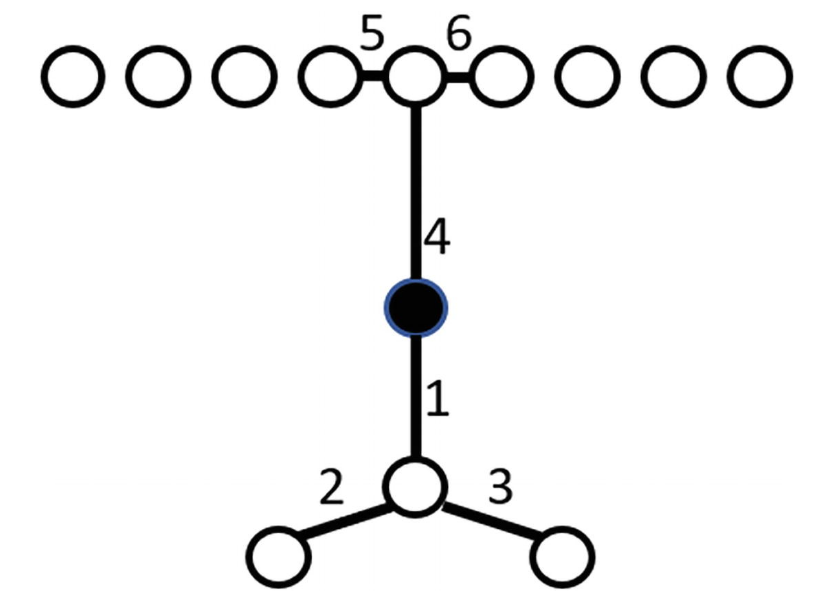
对于上图这个例子，我们介绍这样一种算法。对于任意一个给定的数据点， 例如图中黑点，找到与之最相邻的点，以路径连接它们并标记为路径 \(1\)（如图所示）。将黑点与新连接的点视作一个整体，在所有未与它们相连的点中找到与之相邻的最近的点，再将它们连接并标记为路径 \(2\)（如图所示）。重复这种操作，直到达到最初设定的所需搜寻的点的数量为止。
在建立好上述连接之后，我们可以进行权重运算得到 COF 的值，对于更早的路径（例如路径 \(1\) 早于 路径 \(2\)）赋予更大的权重，更高的 COF 值代表这个点更有可能是一个异常值。
Local Outlier Correlation Integral (LOCI)
Local Outlier Correlation Integral 是一个类似于 LOF 和 COF 的基于密度的异常值检测法。一个最主要的区别在于，LOCI 提供了一种自动判别一个数据点是否为异常值的方法，这意味着我们无需提供数据以外的任何信息（Papadimitriou, 2002）。对于 LOF 与 COF，前者我们需要先行规定一个邻域大小，后者我们需要先行规定搜寻点的数量。相比之下，LOCI 并不需要提前规定邻域的范围，它采用了一种测度 \(alpha(\alpha)\) 以表示邻域的大小，其中 \(\alpha \in (0, 1)\)，默认值 \(\alpha = 0.5\)。
除去 \(\alpha\)，我们还需要一个变量 \(r\)，以代表样本邻域（sampling neighborhood）的距离，所谓样本邻域即对于一个给定的点，我们用来与之比较的点集。具体来说，我们基于一个半径为 \(\alpha \cdot r\) 的有界超球，也被称为 counting neighborhood，通过确定在超球范围内相邻点的数量来判断一个点是否为异常点。
我们令数据集为 \(S = \left\{ p_{1}, p_{2}, \ldots \right\}\)，令数据点 \(p_{i}, p_{j}\) 间的距离为 \(d(p_{i}, p_{j}) \geq 0\)，其中度量 \(d\) 可以任意选取，但除去非负性，还必须满足度量（metric）的基本三定义，即：
Definition. \(r-neighbors\)
对于给定点 \(p_{i} \in S\)，定义其 \(r-neighbors\) 为被包含在以 \(p_{i}\) 为中心，以 \(r\) 为半径的闭球 \(\bar{B}_{r}(p_{i})\) 之中的所有数据点，记作 \(\mathcal{N}(p_{i}, r)\)，即：
其中 \(k\) 为数据的维度。
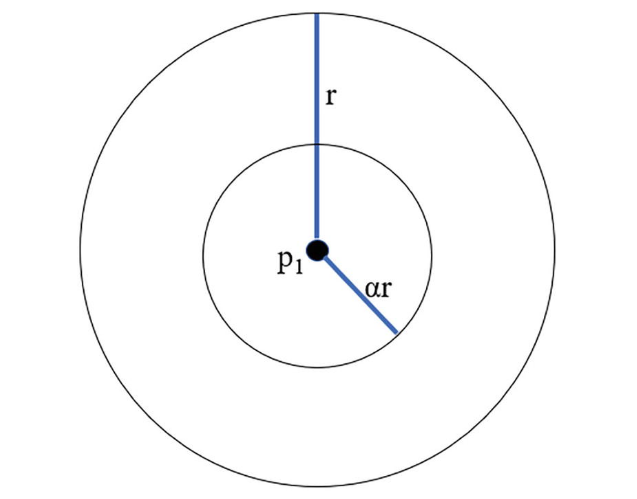
如上图所示，在二维平面上，半径为 \(r\) 的圆代表 sampling neighborhood，半径为 \(\alpha \cdot r\) 的圆代表 counting neighborhood。我们通过计算在 counting neighborhood 范围内的数据点的数量，来表示给定数据点周围的点的聚集拥挤程度。我们对于 sampling neighborhood 中其它每一个点都重复此操作，这样我们能够比较给定点与其它点所在范围的拥挤程度。
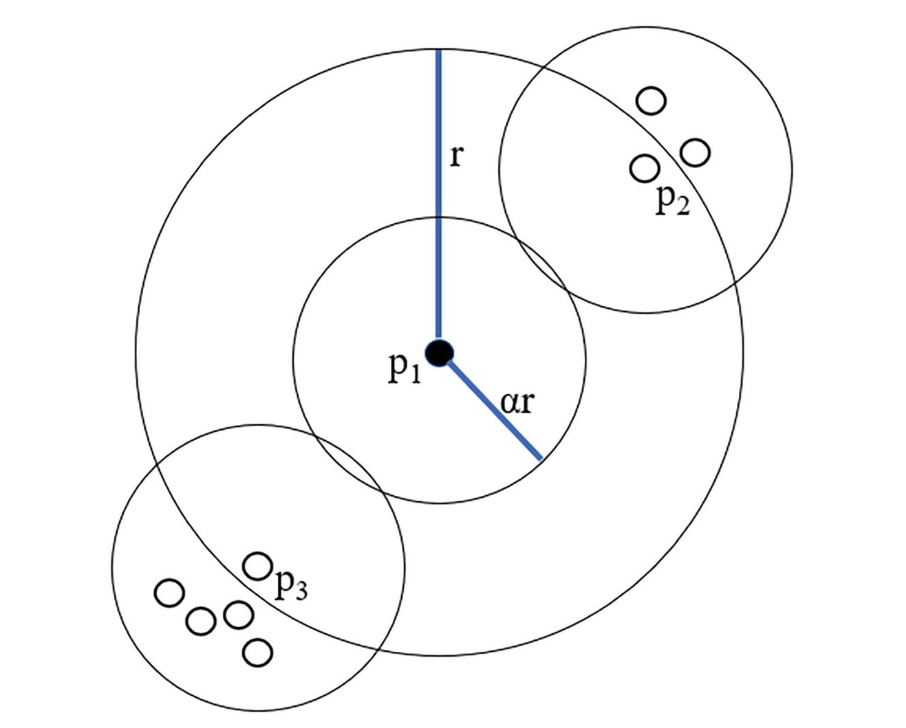
如上图所示，\(p_{1}\) 是我们选中的点，注意到 \(p_{2}, p_{3}\) 两点也在 \(p_{1}\) 的 sampling neighborhood 中（半径为 \(r\) 的圆），同时也分别画出 \(p_{1}, p_{2}, p_{3}\) 的 counting neighborhood（半径为 \(\alpha \cdot r\) 的小圆）。在各自的 counting neighborhood 中，我们观察到 \(p_{1}\) 拥有 \(1\) 个这样的数据点（即它自身），\(p_{2}\) 拥有 \(3\) 个，\(p_{3}\) 拥有 \(5\) 个。
我们定义以点 \(p_{i}\) 为中心，半径为 \(r\) 的 \(r-neigbors\) 中所包含点的个数为 \(n(p_{i}, r)\)，即：
则对于点 \(p_{i}\)，其半径为 \(\alpha \cdot r\) 的 counting neighborhood \(\alpha r - neigbors\) 中包含的点的个数为 \(n(p_{i}, \alpha r)\)。
例如对于上图：
对于给定的数据点，我们可以计算它的 sampling neighborhood 中的平均 \(\alpha r - neighbors\)，记作 \(\hat{n}(p_{i}, r, \alpha)\)，即：
对于上例，我们有：
Multi-granularity Deviation Factor (MDEF)
多粒度偏离因子（Multi-granularity Deviation Factor）应用上述的公式进行计算：
换言之，我们将给定数据点的 \(\alpha r - neighbors\) 与它 sampling neighborhood 中的平均 \(\alpha r - neighbors\) 进行比较。在上例中，我们有：
定义 \(\sigma_{\hat{n}}(p_{i}, r, \alpha)\) 为数据点 \(p_{i}\) 的 sampling neighborhood 中所有点的 counting neighborhood 中包含点的数量的标准差，即：
在上例中，\(\sigma_{\hat{n}}(p_{1}, r, \alpha)\) 为：
定义 MDEF 的标准差 \(\sigma_{\text{MDEF}}(p_{i}, r, \alpha)\) 为：
在得到 \(MDEF(p_{i}, r, \alpha)\) 的标准差之后，我们需要除 \(\alpha\) 外的另一个参数 \(k_{\sigma}\)，代表我们所取的 MDEF 的标准差的个数，若点 \(p_{i}\) 的 \(MDEF(p_{i}, r, \alpha)\) 值超过 \(k_{\sigma}\) 个 MDEF 的标准差，我们认为它是一个异常值，即：
原论文中 \(k_{\sigma}\) 的默认值为 \(3\)（Papadimitriou, 2002），如此选取的原因参考以下引理。
Lemma. (Deviation probability bounds)
对于任意一个数据集中两两点的距离的分布，以及其中任意一点 \(p_{i}\)，我们有：
Proof.
由 Chebyshev’s inequality，我们有：
切比雪夫不等式是一个相对宽松的界，但是它独立于两两距离距离的分布情况而成立。若数据集中点的两两距离的分布已知，实际的界将收紧。例如，若 neighborhood sizes 服从正态分布，且我们选取 \(k_{\sigma} = 3\)，根据 Chebyshev’s inequality，大约有 \(\frac{1}{9}\) 的数据点将被视为异常点，但是实际上被视作异常值的点的个数将远远小于 \(0.01\)。
Copula-Based Outlier Detection (COPOD)
Copula 是一种提供灵活与通用的生成给定单变量边际分布的多元分布的方法。由于边际分布已确定，联合分布则能通过这已确定的边际分布变换到单位立方体 cube: \([0, 1]^{n}\) 上。具体请参考：Copula - 车天健 - 博客园 (cnblogs.com)。一个数据集中可能包含多个随机变量，这便存在两个问题：第一，我们不一定能够知道各个变量的分布，例如一个由 \(X \times Y\) 生成的数据集，\(X \sim N(\mu, \sigma^{2})\)，而 \(Y \sim Beta(\alpha, \beta)\)，在更极端的情况下我们甚至连边缘分布的类型都不知道；第二，我们不一定能知道变量之间的相关性，例如，在 ”\(\text{身高} \times \text{体重}\)“ 的数据集中，粗暴地假设体重独立于身高是不合理。简单来说，Copula 允许我们仅仅通过随机变量 \(X_{1}, X_{2}, \ldots, X_{d}\) 各自的边缘分布，来大致描述其联合分布 \((X_{1}, X_{2}, \ldots, X_{d})\)。
COPOD 通过拟合 Empirical Copula，由于 Copula 本质是一个多元累积分布函数，那么此 Empirical Copula 即是一个 Empirical Cumulative Distribution Function（ECDF，经验 CDF）。令 \(X\) 是一个 \(d\) 维数据集且拥有 \(n\) 个 observation，我们使用 \(X_{i}\) 表示第 \(i\) 个 observation，\(X_{j}\) 表示第 \(j\) 个维度，\(X_{j, i}\) 来表示第 \(i\) 个 observation 在第 \(j\) 维度上的值。
经验 CDF \(\hat{F}(x)\) 定义为：
Theorem.
令 \(X\) 为连续随机变量，其 CDF 为 \(F\)，那么 \(F_{X}(X) \sim \text{Unif}[0, 1]\)。
Proof.
首先， \(F_{X}\) 为累积分布函数，则 \(F_{X}(X) \in [0, 1]\)。令 \(Y = F_{X}(X)\)，那么：
因此 \(F(X) \sim \text{Unif}[0, 1]\)。
Inverse Sampling
我们可以通过均匀分布以逆变换（inverse transform）生成任意所需的分布。例如，有均匀随机变量 \(U \sim \text{Unif}[0, 1]\)，那么 \(F^{-1}(U)\) 服从于分布 \(F\)。这有两种理解方式：
-
由以上 Theorem. 可知，若 \(X\) 是连续随机变量且 CDF 为 \(F_{X}\)，那么 \(F_{X}(X) \sim \text{Unif}[0, 1]\)，则 \(U \sim \text{Unif}[0, 1]\) 同分布于随机变量 \(F_{X}(X)\)。因此，\(F_{X}^{-1}(U)\) 同分布于 \(F_{X}^{-1}(F_{X}(X)) = X\)，服从于分布 \(F_{X}\)。
-
令 \(Y = F_{X}^{-1}(U)\)，则：
\[\begin{align*} P(Y \leq y) & = P(F_{X}^{-1}(U) \leq y) \\ & = P(F_{X}(F_{X}^{-1}(U)) \leq F_{X}(y)) \qquad (F_{X} \text{ is monotonically increasing}) \\ & = P(U \leq F_{X}(y)) \\ \end{align*} \]注意到 \(F_{X}(y)\) 是一个常数，则 \(P(U \leq F_{X}(y)) = F_{U}(F_{X}(y)) = F_{X}(y)\)，因此：
\[P(Y \leq y) = F_{X}(y) \]所以 \(Y = F_{X}^{-1}(U)\) 服从于分布 \(F_{X}\)。
我们令一个 \(d\) 维 copula: \(C: [0, 1]^{d} \rightarrow [0, 1]\)，为一个随机向量 \(\vec{U} = (U_{1}, U_{2}, \ldots, U_{d})\) 的 CDF，其中 \(U_{i} \sim \text{Unif}[0, 1], ~ \forall 1 \leq i \leq d\)，记作：
结合上述 Theorem，我们有：
即 Sklar’s Theorem。
对于维度 \(j\)，由 inverse transformation 有：
通过上述 inverse transformation，我们可以得到 empirical copula \(\hat{U}^{i}\)：
结合经验 CDF 表达式，我们能得到 empirical copula：
通过 COPOD 实现异常值检验一共分为三个步骤：
-
根据数据集 \(X = ( X_{1, i}, X_{2, i}, \ldots, X_{d, i}), ~ 1 \leq i \leq n\) 计算 ECDF（经验 CDF），对于任意数据点，ECDF 给出在统计经验上随机变量取值将小于这个点的概率。
-
通过上述生成的 ECDF，得出 Empirical Copula Function，从而将随机变量的联合概率分布转换为边缘分布。
-
使用上述得到的 Empirical Copula Function 估计尾部概率（Tail Probability），即 \(\forall x_{i}: ~ F_{X}(\vec{x_{i}}) = P \big( X_{1} \leq x_{1, i}, \ldots, X_{d} \leq x_{d, i} \big)\)。
Empirical CDF Outlier Detection (ECOD)
假设有独立同分布生成的样本数据 \(X_{1}, X_{2}, \ldots, X_{n} \in \mathbb{R}^{d}\)，且数据点维度为 \(d\)，即矩阵数据集 \(\mathbf{X} \in \mathbb{R}^{n \times d}\)。
Definition. Left and Right tail ECDF
Left and right tail ECDF 分别定义为，在某一个维度（例如 \(j\)）上的传统 CDF 以及 survival function，即对于 \(z \in \mathbb{R}\)：
Definition. Sample Skewness Coefficient
对于某一个维度（例如 \(j\)），这个维度上的 sample skewness coefficient 定义为：
其中 \(\overline{X^{(j)}} = \frac{1}{n} \sum\limits_{i=1}^{n}X_{i}^{(j)}\) 为第 \(j\) 个特征（维度）的样本均值。
Definition. Aggregated Tail Probability
对于数据点 \(X_{i} \in \mathbf{X}\) ，定义其以下三种 aggregated tail probability：
Definition. Outlier Score
对于数据点 \(X_{i} \in \mathbf{X}\) ，定义其 outlier score 为以上三种 aggregated tail probability 的最大值：
代码实现如下：
import numpy as np
class ECOD(object):
def __init__(self, data: np.array):
if len(data.shape) == 1:
data = data.reshape(-1, 1)
self.data = data
self.size, self.dim = self.data.shape
for p in self.data:
try:
assert len(p) == self.dim
except:
raise AssertionError("Sample dimensions should be identical.")
def ecdf(self, x, d: int) -> dict:
try:
assert 0 <= d < self.dim
except:
raise AssertionError("Incorrect dimension appointed.")
left = np.sum(self.data[:, d] <= x) / self.size
right = np.sum(self.data[:, d] >= x) / self.size
return {"left": left, "right": right}
def skewness(self, d: int) -> float:
try:
assert 0 <= d < self.dim
except:
raise AssertionError("Incorrect dimension appointed.")
avg = np.mean(self.data[:, d])
nominator = np.mean((self.data[:, d] - avg) ** 3)
denominator = np.power((np.sum((self.data[:, d] - avg) ** 2) / (self.size - 1)), 1.5)
return nominator / denominator
def aggregate(self, p: np.array) -> dict:
left, right, auto = [], [], []
for j in range(self.dim):
prob = self.ecdf(x=p[j], d=j)
left.append(np.log(prob["left"]))
right.append(np.log(prob["right"]))
if self.skewness(j) < 0:
auto.append(np.log(prob["left"]))
else:
auto.append(np.log(prob["right"]))
return {"left": -np.sum(left), "right": -np.sum(right), "auto": -np.sum(auto)}
def score(self, p) -> float:
return np.max(list(self.aggregate(p=p).values()))
def execute(self, onum: int):
scores = list(map(lambda p: self.score(p=p), self.data))
idx = np.argsort(scores)[::-1][:onum]
return self.data[idx]
本文来自博客园，作者：车天健，转载请注明原文链接：https://www.cnblogs.com/chetianjian/p/17466788.html
