对马尔科夫决策过程的代码补充解释

　　这篇文章是https://www.cnblogs.com/chester-cs/p/12928649.html的代码补充解释，这里我仅仅实现了Value迭代，Policy迭代读者可以尝试自己实现。

　　学习了MDP即马尔科夫决策过程之后我就想用代码实现实现，想看看机器是如何不断优化自身的。

　　考虑这样一个世界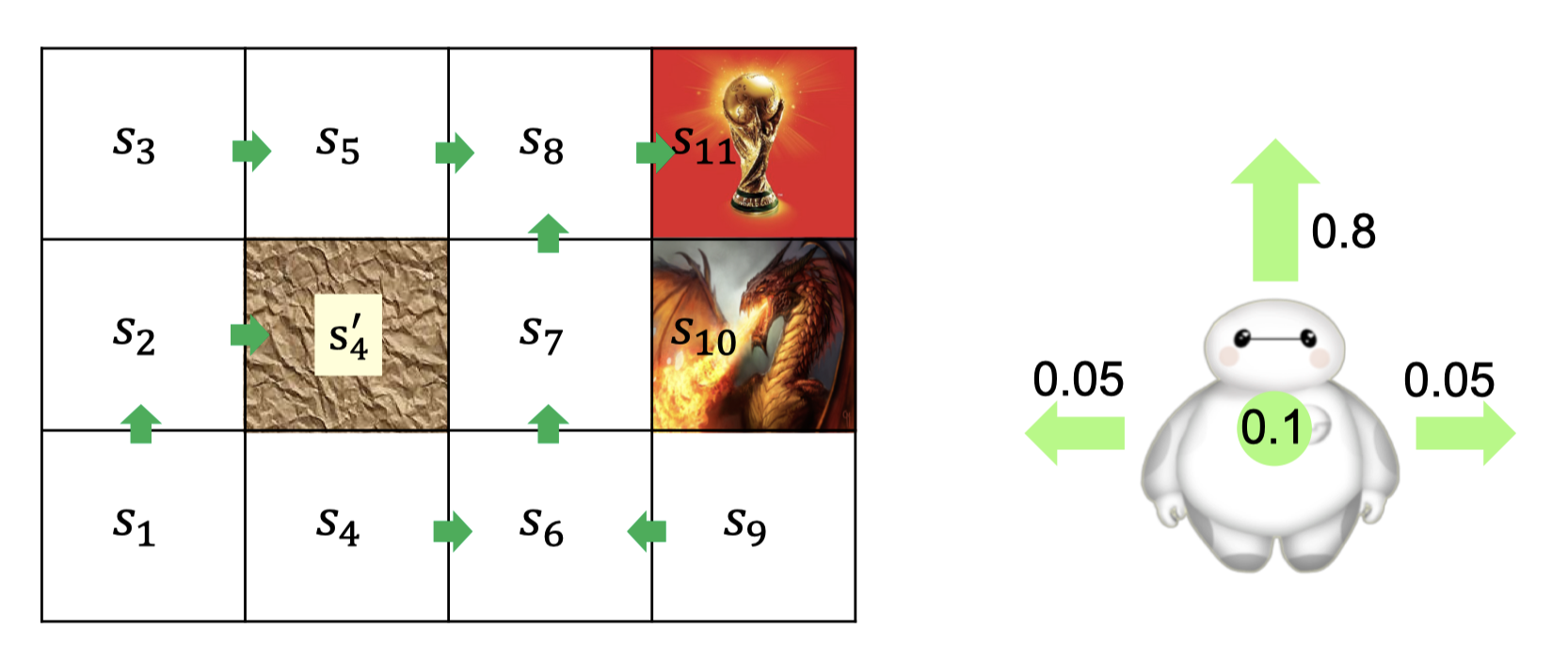：　　有奖励，有陷阱，有阻碍。给Agent发出指令后Agent的行为是非确定的。

　　这个问题和更常见的“增强学习问题”的差别在哪里？

　　1. 状态空间是有限的，离散的。而有很多“增强学习问题”是状态连续的，状态无穷的

　　2. 动作空间是有限的，离散的。而有很多“增强学习问题”是动作连续的

　　3. 由（1）（2），我们能够以矩阵形式保存每个状态下每个动作的$Q$值即$Q(s,a)$。当状态、动作空间很大的时候这是不现实的，我们可以采用人工神经网络等方法来拟合$Q$。

　　有了以上的思考，我们也不考虑这么多了，看一下这个典型的MDP，优化后是什么样。我写了一个ipynb文件。

## 使用value-iteration来寻找最优策略，其中更改reward-function使得agent采取永远不会输的策略
import numpy as np

P = np.zeros((11,4,11))
V = np.zeros(11)
Q = np.zeros((11,4))
R = np.zeros((11,4))

## 定义转移概率矩阵
P[0] = np.array([[0.15,0.8,0,0.05,0,0,0,0,0,0,0],[0.95,0,0,0.05,0,0,0,0,0,0,0],[0.95,0.05,0,0,0,0,0,0,0,0,0],[0.15,0.05,0,0.8,0,0,0,0,0,0,0]])
P[1] = np.array([[0,0.2,0.8,0,0,0,0,0,0,0,0],[0.2,0.8,0,0,0,0,0,0,0,0,0],[0.05,0.9,0.05,0,0,0,0,0,0,0,0],[0.05,0.9,0.05,0,0,0,0,0,0,0,0]])
P[2] = np.array([[0,0,0.95,0,0.05,0,0,0,0,0,0],[0,0.8,0.15,0,0.05,0,0,0,0,0,0],[0,0.05,0.95,0,0,0,0,0,0,0,0],[0,0.05,0.15,0,0.8,0,0,0,0,0,0]])
P[3] = np.array([[0.05,0,0,0.9,0,0.05,0,0,0,0,0],[0.05,0,0,0.9,0,0.05,0,0,0,0,0],[0.8,0,0,0.2,0,0,0,0,0,0,0],[0,0,0,0.2,0,0.8,0,0,0,0,0]])
P[4] = np.array([[0,0,0.05,0,0.9,0,0,0.05,0,0,0],[0,0,0.05,0,0.9,0,0,0.05,0,0,0],[0,0,0.8,0,0.2,0,0,0,0,0,0],[0,0,0,0,0.2,0,0,0.8,0,0,0]])
P[5] = np.array([[0,0,0,0.05,0,0.1,0.8,0,0.05,0,0],[0,0,0,0.05,0,0.9,0,0,0.05,0,0],[0,0,0,0.8,0,0.15,0.05,0,0,0,0],[0,0,0,0,0,0.15,0.05,0,0.8,0,0]])
P[6] = np.array([[0,0,0,0,0,0,0.15,0.8,0,0.05,0],[0,0,0,0,0,0.8,0.15,0,0,0.05,0],[0,0,0,0,0,0.05,0.9,0.05,0,0,0],[0,0,0,0,0,0.05,0.1,0.05,0,0.8,0]])
P[7] = np.array([[0,0,0,0,0.05,0,0,0.9,0,0,0.05],[0,0,0,0,0.05,0,0.8,0.1,0,0,0.05],[0,0,0,0,0.8,0,0.05,0.15,0,0,0],[0,0,0,0,0,0,0.05,0.15,0,0,0.8]])
P[8] = np.array([[0,0,0,0,0,0.05,0,0,0.15,0.8,0],[0,0,0,0,0,0.05,0,0,0.95,0,0],[0,0,0,0,0,0.8,0,0,0.15,0.05,0],[0,0,0,0,0,0,0,0,0.95,0.05,0]])
P[9] = np.array([[0,0,0,0,0,0,0,0,0,1,0],[0,0,0,0,0,0,0,0,0,1,0],[0,0,0,0,0,0,0,0,0,1,0],[0,0,0,0,0,0,0,0,0,1,0]])
P[10] = np.array([[0,0,0,0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0,0,0,1]])

## 定义reward-function
punishment = -100
reward = 100
R[0] = np.array([0,0,0,0])
R[1] = np.array([0,0,0,0])
R[2] = np.array([0,0,0,0])
R[3] = np.array([0,0,0,0])
R[4] = np.array([0,0,0,0])
R[5] = np.array([0,0,0,0])
R[6] = np.array([0.05*punishment,0.05*punishment,0,0.8*punishment])
R[7] = np.array([0.05*reward,0.05*reward,0,0.8*reward])
R[8] = np.array([0.8*punishment,0,0.05*punishment,0.05*punishment])
R[9] = np.array([0,0,0,0])
R[10] = np.array([0,0,0,0])

for j in range(100):
    for s in range(9):
        for a in range(4):
            Q[s][a] = R[s][a]+0.9*P[s][a]@V
        V[s] = np.max(Q[s])
print('Print policy(With punish:-100,reward:100): ')
for l in range(9):
    print('State' + str(l+1) +': '+ str(np.argmax(Q[l])))

　　一共11个状态0-10，定义了每个状态的价值$V$，状态价值矩阵$Q(s,a)$，以及概率转移矩阵$P$。0-3的动作分别表示向上下左右行走。

　　价值矩阵是长度为11的向量，状态动作矩阵是11×4的矩阵。这两个都好理解对不对。而状态转移矩阵我定义成了11×4×11，是这样来用的，前一个状态共有11个，那么有4个动作可选，选每个动作后下一个状态又是“非确定的”（因为我这个游戏的限制！）所以转移后的状态也应该是一个向量的概率分布。

　　我分别用拿到奖杯奖励100，被龙杀死惩罚100。和奖励100惩罚10000，来进行价值迭代，得到的结果是不同的。

Print policy(With punish:-100,reward:100): 
State1: 0
State2: 0
State3: 3
State4: 3
State5: 3
State6: 0
State7: 0
State8: 3
State9: 2

---

 

Print policy(With punish:-10000,reward:100): 
State1: 0
State2: 0
State3: 3
State4: 2
State5: 3
State6: 2
State7: 2
State8: 3
State9: 1

　　拿状态9来看，惩罚小的时候，agent会大线条的直接向左走，因为这样能更快吃到奖杯啊，被杀死的概率也不大。当惩罚大的时候，agent学谨慎了，一直向下走。因为它学到了向左走有0.05的概率被惩罚到倾家荡产，而向下走虽然慢却稳健安全。

　　拿状态4来看，惩罚小的时候，agent会直接向右走，因为这样离奖杯更近。当惩罚大的时候agent显然明白了右边是危险的，直接调转方向向左走了。状态6、7更明显，agent宁愿一直对着墙走也不愿冒被惩罚的风险。

　　Agent的智能不就在这迭代中获得了吗~~~