深度学习中损失函数之RMS和MES

　　学校给我们一人赞助了100美元购买英文原版图书，几方打听后选择了PRML 即Pattern Recognition and Machine Learning。自从拆封这本书开始慢慢的品读，经常会有相见恨晚之感。虽然目前我只是慢慢地阅读了前几个小节，也知道后面的章节会越来越晦涩，但是还是下定决心一定要把这本书弄透彻。这篇文章是在阅读引章：曲线拟合时发现的问题。想记录下来学到的两个点，并对一道课后习题作解析。

　　第一节是曲线拟合，曲线拟合是深度学习问题中的regression问题，即回归问题。其他的问题据我了解还有classification问题，即分类问题和clustering问题，即聚类问题。regression问题很显然是一个有监督学习。给你一系列点x，再给你一系列这些点对应的target，我们的目标是找到一个函数使得target和我们预测的x之间的误差最小。

　　在这一节是以一个正弦函数为例，给出正弦曲线上加上了随机误差的一系列点。我们选择多项式拟合polynomial fitting：$$y(x,\textbf{w})=w_0+w_{1}x+w_{2}x^{2}+\cdots+w_{M}x^{M}=\sum_{j=0}^M w_j x^j$$

　　现在我们要解决的问题有三个：

　　1.什么叫误差？既然我们的目标是让误差最小，那么误差函数error function(或者是loss function?)应该长什么样？

　　2.有了误差函数，怎么样确定多项式的系数coefficients来使得误差函数最小。

　　3.多项式的次数order应该怎么选择？

　　下面一一进行解答：

　　1.首先我们选用了一类简单而且广泛被使用的error function--SSE，即和方差。我们的目标是最小化以下的目标error function(SSE):$$E(\textbf{w})=\frac{1}{2} \sum_{n=1}^{N} \left\{y(x_n ,\textbf{w})-t_n \right\}^2$$从直观上可以看到，这个损失函数是正定的，而且它的值越小，预测值和target值间的差距就越小，相应的，拟合效果就越好。其中$\frac{1}{2}$是为了方便计算，还可以选为其他值。我们的问题转化为了最小化误差函数。

　　2.已经交代过，我们采用多项式拟合，那么模型的参数就是多项式的系数$w_{0}~w_{M}$。怎样确定模型参数使得error function最小呢？这里的解法很特殊。我们使用的是最小平方误差，那么对误差函数关于多项式系数进行求导，得到的结果将是关于系数$\textbf{w}$的线性函数(我有一个理解，其实就是让loss对w向量求梯度，是不是呢？以后应该能回答)。为了求取极小值，在这里我们是可以让这个导数为$\textbf{0}$，从而获得解析形式的解$w^{*}$，(这里和之前模式识别课上学的那个什么伪逆解是不是有些关系？也是解析解)。具体细节在PRML中体现在课后习题，在后面讲。

　　3.现在我们能够对一个给定次数的多项式求出使error function最小的参数了，还没有解决的问题是，多项式的order应该如何选择？将这个问题推广就变成了一个模型选择的问题，使用更高次数的多项式一定能对样本点进行最好的拟合，进而获得最佳的泛化性能吗？下面的的几张图能够说明问题。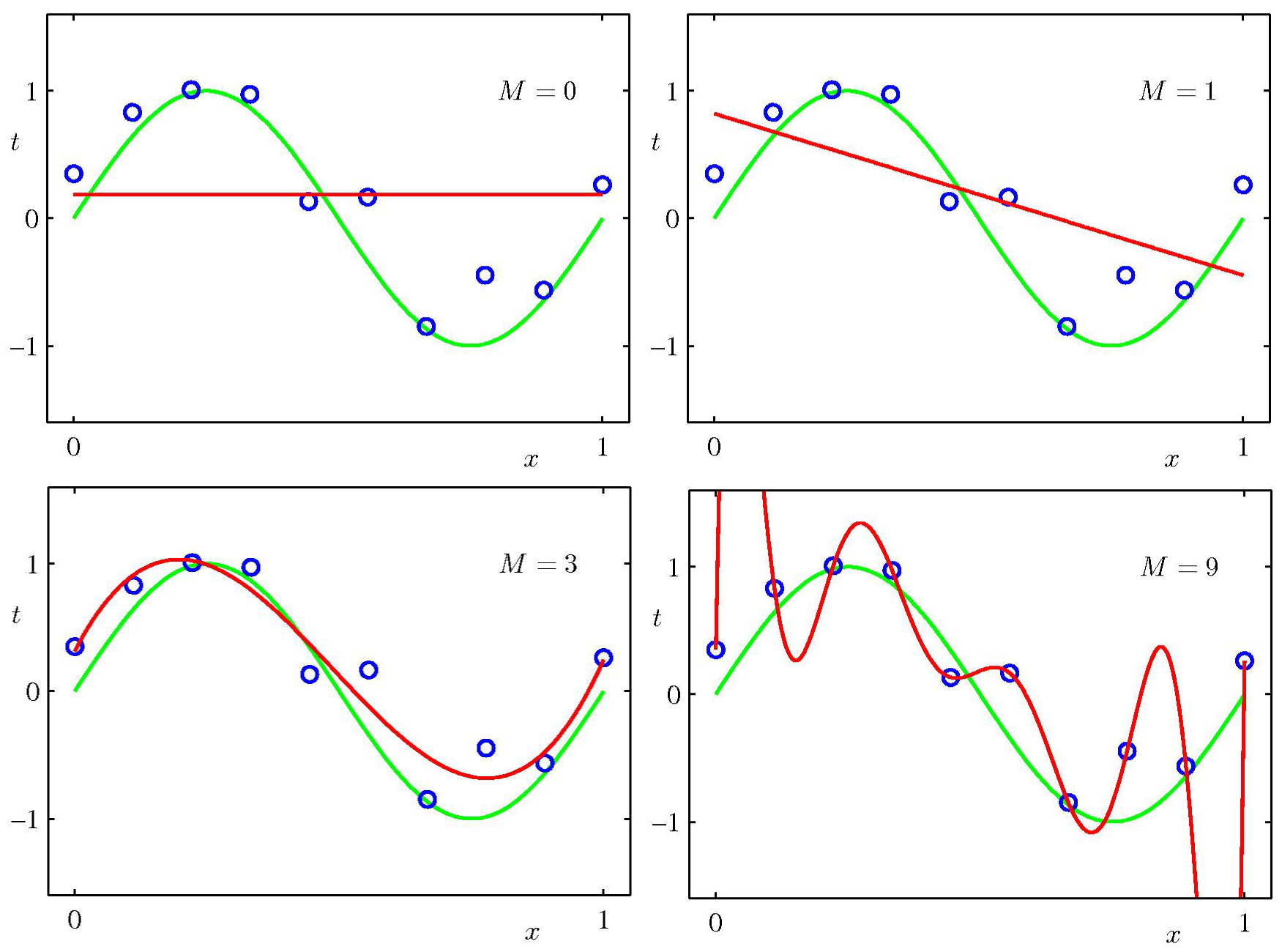

 　　我们看到，当M比较小时，拟合效果很差，随着M增加(如M=3)，能够进行较好的拟合。但是当M达到9时，因为对十个样本点，9次多项式能够唯一确定。拟合曲线却在样本点之间发生了剧烈的振荡，不能够获得很好的泛化性能。原因是出现了over-fitting过拟合。此时的曲线对随机的噪声非常敏感，且不具有任何的灵活性。当样本点增加后，这种过拟合现象得到了极大的缓解。此时为了让不同大小的数据集产生的误差函数的有相同的比例和单位。我们选用RMS error function:$$E_{RMS} = \sqrt{2E(\textbf{w* })/N}$$