使用torch实现RNN
(本文对https://blog.csdn.net/out_of_memory_error/article/details/81456501的结果进行了复现。)
在实验室的项目遇到了困难,弄不明白LSTM的原理。到网上搜索,发现LSTM是RNN的变种,那就从RNN开始学吧。
带隐藏状态的RNN可以用下面两个公式来表示: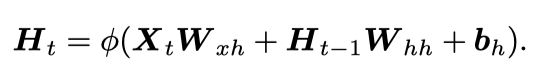
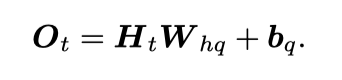
可以看出,一个RNN的参数有W_xh,W_hh,b_h,W_hq,b_q和H(t)。其中H(t)是步数的函数。
参考的文章考虑了这样一个问题,对于x轴上的一列点,有一列sin值,我们想知道它对应的cos值,但是即使sin值相同,cos值也不同,因为输出结果不仅依赖于当前的输入值sinx,还依赖于之前的sin值。这时候可以用RNN来解决问题
用到的核心函数:torch.nn.RNN() 参数如下:
-
input_size – 输入
x的特征数量。 -
hidden_size – 隐藏层的特征数量。
-
num_layers – RNN的层数。
-
nonlinearity – 指定非线性函数使用
tanh还是relu。默认是tanh。 -
bias – 如果是
False,那么RNN层就不会使用偏置权重 $b_ih$和$b_hh$,默认是True -
batch_first – 如果
True的话,那么输入Tensor的shape应该是[batch_size, time_step, feature],输出也是这样。 -
dropout – 如果值非零,那么除了最后一层外,其它层的输出都会套上一个
dropout层。 -
bidirectional – 如果
True,将会变成一个双向RNN,默认为False。
下面是代码:
1 # encoding:utf-8 2 import torch 3 import numpy as np 4 import matplotlib.pyplot as plt # 导入作图相关的包 5 from torch import nn 6 7 8 # 定义RNN模型 9 class Rnn(nn.Module): 10 def __init__(self, INPUT_SIZE): 11 super(Rnn, self).__init__() 12 13 # 定义RNN网络,输入单个数字.隐藏层size为[feature, hidden_size] 14 self.rnn = nn.RNN( 15 input_size=INPUT_SIZE, 16 hidden_size=32, 17 num_layers=1, 18 batch_first=True # 注意这里用了batch_first=True 所以输入形状为[batch_size, time_step, feature] 19 ) 20 # 定义一个全连接层,本质上是令RNN网络得以输出 21 self.out = nn.Linear(32, 1) 22 23 # 定义前向传播函数 24 def forward(self, x, h_state): 25 # 给定一个序列x,每个x.size=[batch_size, feature].同时给定一个h_state初始状态,RNN网络输出结果并同时给出隐藏层输出 26 r_out, h_state = self.rnn(x, h_state) 27 outs = [] 28 for time in range(r_out.size(1)): # r_out.size=[1,10,32]即将一个长度为10的序列的每个元素都映射到隐藏层上. 29 outs.append(self.out(r_out[:, time, :])) # 依次抽取序列中每个单词,将之通过全连接层并输出.r_out[:, 0, :].size()=[1,32] -> [1,1] 30 return torch.stack(outs, dim=1), h_state # stack函数在dim=1上叠加:10*[1,1] -> [1,10,1] 同时h_state已经被更新 31 32 33 TIME_STEP = 10 34 INPUT_SIZE = 1 35 LR = 0.02 36 37 model = Rnn(INPUT_SIZE) 38 print(model) 39 40 loss_func = nn.MSELoss() # 使用均方误差函数 41 optimizer = torch.optim.Adam(model.parameters(), lr=LR) # 使用Adam算法来优化Rnn的参数,包括一个nn.RNN层和nn.Linear层 42 43 h_state = None # 初始化h_state为None 44 45 for step in range(300): 46 # 人工生成输入和输出,输入x.size=[1,10,1],输出y.size=[1,10,1] 47 start, end = step * np.pi, (step + 1)*np.pi 48 49 steps = np.linspace(start, end, TIME_STEP, dtype=np.float32) 50 x_np = np.sin(steps) 51 y_np = np.cos(steps) 52 53 x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis]) 54 y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis]) 55 56 # 将x通过网络,长度为10的序列通过网络得到最终隐藏层状态h_state和长度为10的输出prediction:[1,10,1] 57 prediction, h_state = model(x, h_state) 58 h_state = h_state.data # 这一步只取了h_state.data.因为h_state包含.data和.grad 舍弃了梯度 59 # 反向传播 60 loss = loss_func(prediction, y) 61 optimizer.zero_grad() 62 loss.backward() 63 64 # 优化网络参数具体应指W_xh, W_hh, b_h.以及W_hq, b_q 65 optimizer.step() 66 67 # 对最后一次的结果作图查看网络的预测效果 68 plt.plot(steps, y_np.flatten(), 'r-') 69 plt.plot(steps, prediction.data.numpy().flatten(), 'b-') 70 plt.show()
最后一步预测和实际y的结果作图如下:
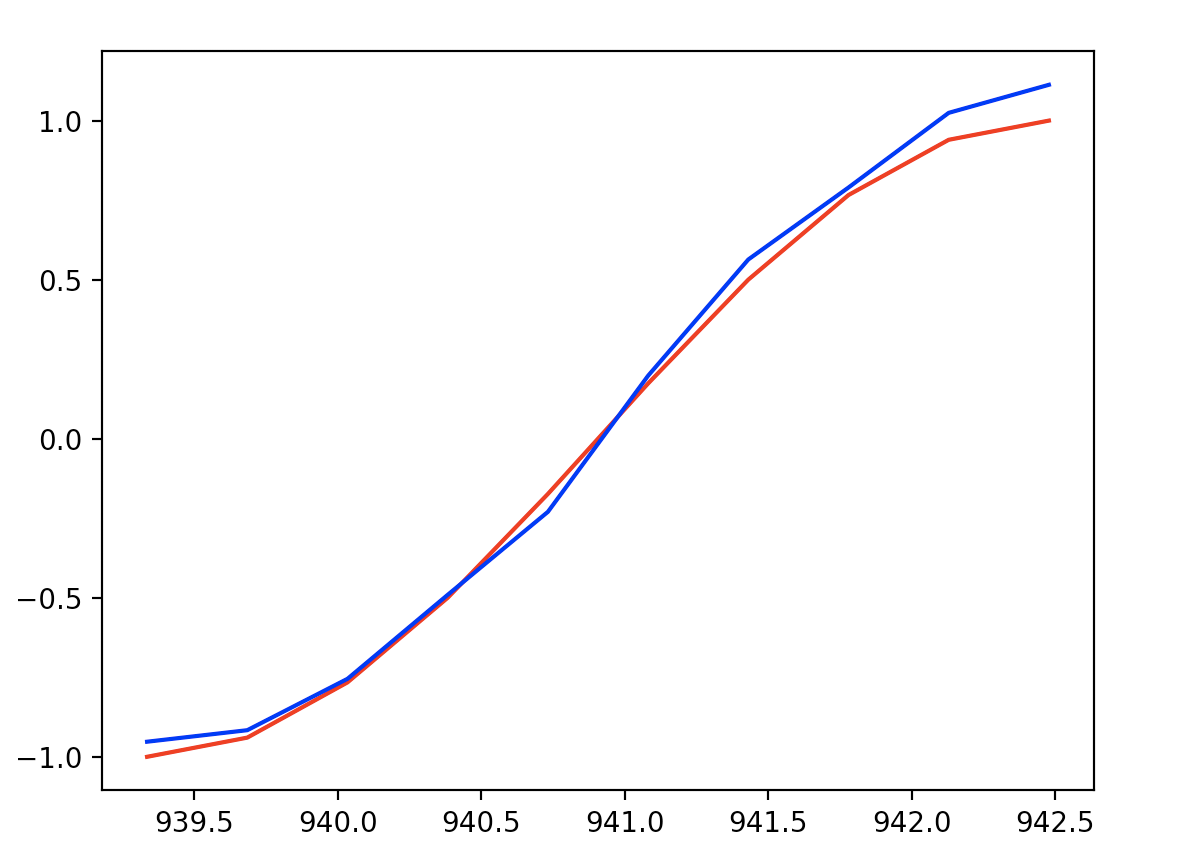
可看出,训练RNN网络之后,对网络输入一个序列sinx,能正确输出对应的序列cosx



