神经网络中激活函数的作用(repost from https://blog.csdn.net/program_developer/article/details/78704224)

　　实验室正在弄一个项目，在读有关论文的时候就发现一个令我疑惑的点：在论文里反复强调了激活函数(又叫做活化函数)的重要性。这让我很迷惑，因为在我当前的认知里，激活函数是一类相当简单的函数，比如relu函数:$f(x)=\max(0,x)$，只是一个分段线性的函数啊，为什么会有如此重要的意义？带着疑问找到了这一篇讲的很好的文章，受益匪浅:https://blog.csdn.net/program_developer/article/details/78704224

　　考虑一个不带激活函数的单层感知机:one-layer perception，它的输入和输出相当简单:$y=w_{1}x_{1}+w_{2}x_{2}+b$。下图是单层感知机的工作原理：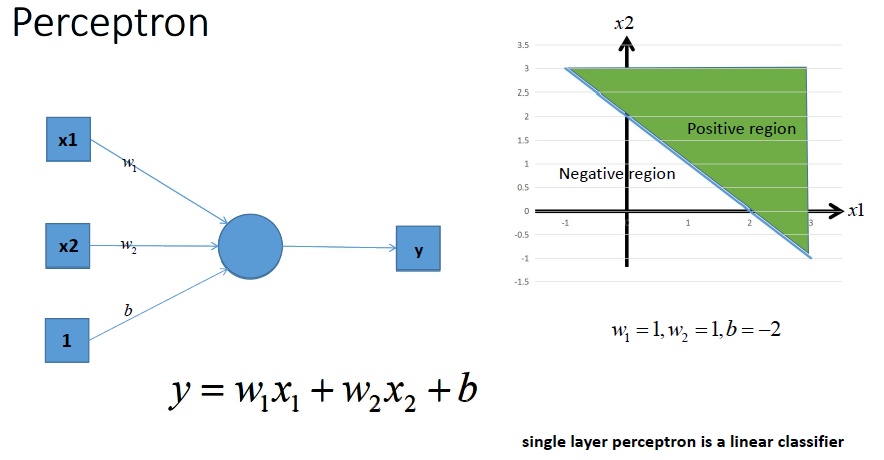

 

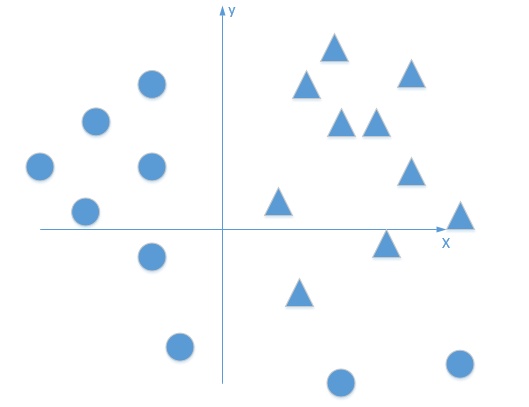
 　　从上图我们可以看出，一个没有激活函数的单层感知机是一个线性分类器，不能解决下图所示的线性不可分的问题。

　　

 

　　 考虑不带激活函数的多个感知机:Perceptron with multiple layers，它的输入输出可以用下面的式子表示:$y=w_{2-1}\left(w_{1-11}x_1+w_{1-21}x_2+b_{1-1}\right)+w_{2-2}\left(w_{1-12}x_1+w_{1-22}x_2+b_{1-2}\right)+w_{2-3}\left(w_{1-13}x_1+w_{1-23}x_2+b_{1-3}\right)$，下面是一个具有单隐藏层的不带激活函数的感知机。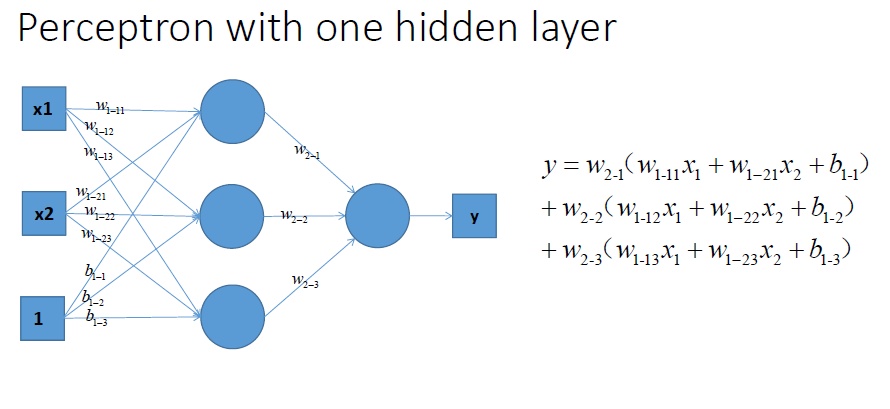

 

 　　对y进行合并同类项，整理之后得到的公式如下:$y=x_1(w_{1-11}w_{2-1}+w_{1-12}w_{2-2}+w_{1-13}w_{2-3})+x2(w_{1-21}w_{2-1}+w_{1-22}w_{2-2}+w_{1-23}w_{2-3})+w_{2-1}b_{1-1}+w_{2-2}b_{1-2}+w_{2-3}b_{1-3}$。我们可以很容易的看到，合并后的式子仍然是一个关于$x_1$和$x_2$的线性分类器，仍然解决不了非线性的问题。

　　考虑带有激活函数的感知机:在所有的隐藏层和输出层之间加一个激活函数，如Sigmoid函数，这样y输出的就是关于x的一个非线性函数了。$a=w_{1}x_{1}+w_{2}x_{2}+b,\quad y=\sigma (a)$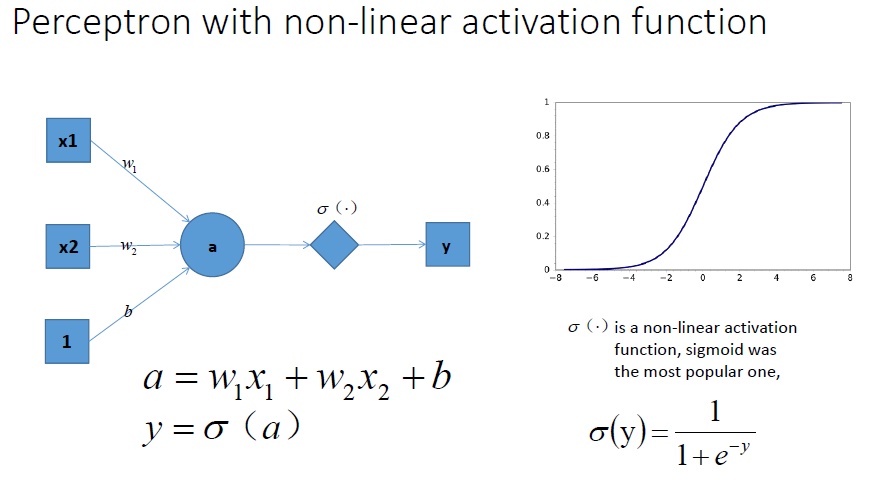

 

 　　如果拓展到带有激活函数的的多个神经元。神经网络的表达能力会更强。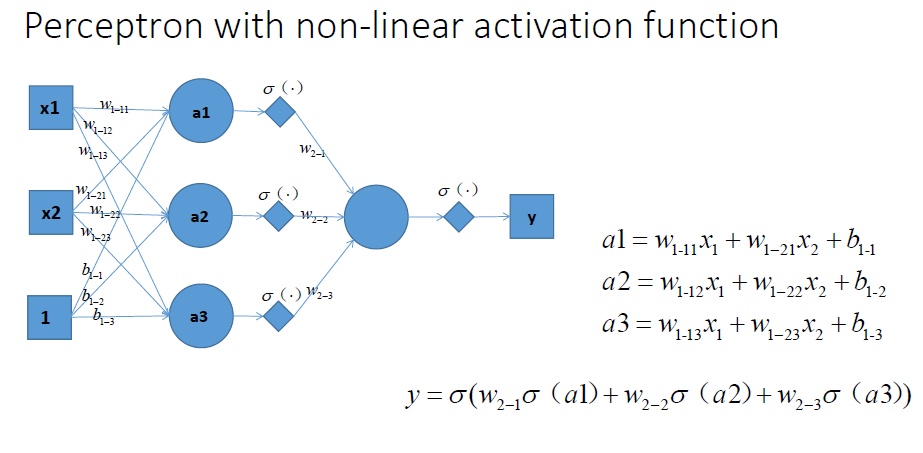

 

 　　下面是带有激活函数的感知机的工作原理：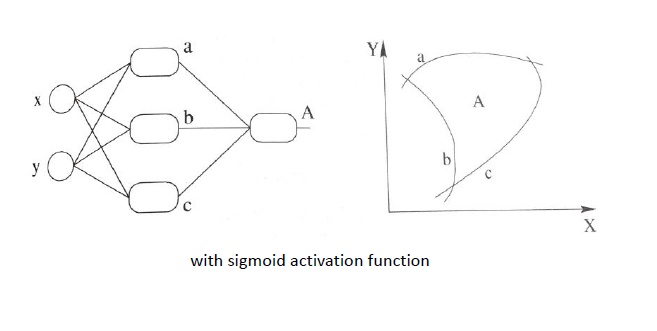

 

 　　可见，非线性的激活函数能够对非线性可分的样本进行分类。

　　总结：激活函数是用来加入非线性因素的，能够提高神经网络对模型的表达能力，尤其是能够解决线性不可分的问题。