离散数学--第十章 群，环，域

群

基本定义

设V=<S, ∘ >是代数系统，∘为二元运算，如果∘运算是可结合的，则称V为半群（代数系统的前提不要忘，详情可看第九章）

如果半群中有单位元==> 含幺半群|独异点

含幺半群还有逆元==>群通常记作G

群中的二元运算可交换==>交换群|阿贝尔群

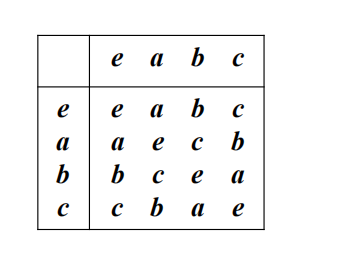
Klein四元群

特征：

1. 满足交换律

2. 每个元素都是自己的逆元

3. a, b, c中任何两个元素运算结果都等于剩下的第三个元素

平凡群

只有单位元

有限群

群中元素有限

子群

如果把群看成集合，子群就是子集中能满足群定义的 一个集合（可以有多个集合）

群是代数系统，最基本要满足封闭性！

真子群就类似真子集

子群判定定理：

设G为群，H是G的非空子集. H是G的子群当且仅当∀a,b∈H 有ab−1∈H（感觉很懵逼） 证 必要性显然. 只证充分性. 因为H非空，必存在a∈H. 根据给定条件得aa−1∈H，即e∈H. 任取a∈H, 由e,a∈H 得 ea−1∈H，即a−1∈H. 任取a,b∈H，知b⁻¹∈H. 再利用给定条件得a(b⁻¹) ⁻¹∈H，即 ab∈H. 综合上述，可知H是G的子群. 

生成子群：

设G为群，a∈G，令H={a^k| k∈Z}，则H是G的子

群，称为由 a 生成的子群，记作<a>

例如：

Klein四元群 G = {e,a,b,c}的所有生成子群是：

<e>={e}, <a>={e,a}, <b>={e,b}, <c>={e,c}.

则偏序集< L(G), ⊆ >称为G的子群格

就相当于子群先变成偏序集然后就满足了格的定义？

因为是子群所以叫子群格？

右（左）陪集

设H是G的子群，a∈G.令

Ha={ha | h∈H}

称Ha是子群H在G中的右陪集. 称a为Ha的代表元素.

相当于右（左）乘a所得的集合？

循环群

设G是群，若在G中存在一个元素a,使得G中

的任意元素都是a的幂，则称该群为循环群，

元素a为循环群G的生成元。记G =<a>.

生成子群就是一个循环群！

G 的子群也是循环群

若G 是无限阶，则G 的子群除{e}外也是无限阶 （{e}是1阶）

若G 是n 阶的，则对于n 的每个正因子d,

在G 中有且仅有一个d 阶子群.

置换群

设S＝{1,2,…,n}，S上的任何双射函数σ：S→S称为S上的n元置换。可以理解为双射函数....

设σ,τ是n元置换，则σ和τ的复合σ°τ也是n元置换，称为σ与τ的乘积，记作στ。就是双射函数的复合函数...

设 π ∈ Sn, π : i1 → i2 , i2 → i3, ⋅⋅⋅, ik → i1 ，并使其余的元

素保持不变，则称 π 为一个k阶循环置换，记为(i₁ i₂⋅⋅⋅ i_k ) 

由于(i1 i2 i3 ⋅⋅⋅ ik ) = (i2 i3 ⋅⋅⋅ ik i1 ) = ⋅⋅⋅ = (ik i1 i2 ⋅⋅⋅ ik-1 ), 因此一个k阶循环置换有 k种表示方式，且k阶循环置换的阶为k

1阶循环置换只有 1 种表示方式，即恒等置换（i）可视作 (i,i) 但是一阶循环置换

2阶循环置换又称为对换

对换分解式：(i1 i2…ik) = (i1 i2) … (i1 ik-1) (i1 ik) 

奇置换：表成奇数个对换之积

偶置换：表成偶数个对换之积

奇置换与偶置换之间存在一一对应，因此各有n!/2个

阶

设G是群，a∈G，使得等式 a^k=e 成立的最小正整数k 称为a 的阶，记作|a|=k，

称 a 为 k 阶元. 若不存在这样的正整数 k，则称 a 为无限阶元

群的阶 <==> 群的基数<==> 群中元素的个数

环与域

设<R,+,·>是代数系统，+和·是二元运算. 如果满足

以下条件:

(1) <R,+>构成交换群 

(2) <R,·>构成半群 | 代数系统中只有结合率

(3) · 运算关于+运算适合分配律 | 有分配率

则称<R,+,·>是一个环

一般有整数环，实数环，复数环，有理数环...

如果半群==>有交换率|环==>交换环 （有交换律的半群不一定是交换群！！！）

如果半群存在单位元环==>环|含幺环

若∀a,b∈R，ab=0 ⇒ a=0∨b=0，则称R是无零因子环 懵？？？

若R既是交换环、含幺环、无零因子环，则称R是整环

设R是整环，且R中至少含有两个元素. 若∀a∈R*，其中R*=R−{0}，都有a^－1∈R，则称R是域

都是概念没啥感觉