AVL树的旋转操作详解

【0】README

0.0） 本文部分idea 转自：http://blog.csdn.net/collonn/article/details/20128205
0.1） 本文仅针对性地分析AVL树的单旋转（左左单旋转和右右单旋转）和双旋转（左右双旋转和右左单旋转）的内部核心技巧；
0.2）不得不提的是，旋转有两个属性： 轴和旋转方向；（旋转轴即是原最小树经过旋转修正后的符合AVL的最小树的根节点）
0.3） 旋转轴的确定： （干货——单双旋转的旋转轴确定问题）

0.3.1）单旋转：旋转轴为不满足AVL条件的最小树的树根的相应孩子节点；
0.3.2）多旋转：旋转轴为不满足AVL条件的最小树的树根的相应孙子节点；

【1】如何判断进行单旋转还是双旋转（什么时候需要单旋转，而什么时候需要多旋转？）

1.0）高度不平衡需要α点的两棵子树高度差为2，故可得高度不平衡可能出现在下面四种情况中：

① 对α的左儿子的左子树进行一次插入。

② 对α的左儿子的右子树进行一次插入。

③ 对α的右儿子的左子树进行一次插入。

④ 对α的右儿子的右子树进行一次插入。

1.1）单旋转： 插入点不介于不满足AVL条件的树根和树根对应孩子节点之间；（情形①、③ 即左-左、右-右）

1.2）双旋转：插入点介于不满足AVL条件的树根和树根对应孩子节点之间；（情形②、④ 即左-右、右-左）

【2】单旋转

2.1）左左旋转（顺时针旋转）： 从插入点回溯到第一个不满足AVL条件的节点；本例中，插入点是10，而第一个不满足AVL条件的节点是30；将回溯路径上的节点除节点30外，上移一层，节点30下移一层；

case1）


	（这是一个左右双旋转特例，当不符合AVL条件的树根和插入点的父节点只有一个子节点，且相反方向的子节点，当然了，插入点要介于树根和插入点父节点之间的话，才满足双旋转特例的条件）

Attention）

A1）因为10 小于 20 且小于30；所以通过一次单旋转就可以完成；
（也即是，左左单旋转时，不满足AVL条件的最小树的根应该下移，该树的其他节点上移，而不管该树的左子树的右孩子或者存在或者不存在，在旋转过程中，都要把该左子树的的右孩子添加以作为最小树根的左孩子，因为即使不存在，添加null 也不影响最后的旋转效果）
case2）

2.2）右右旋转（逆时针旋转）： 从插入点回溯到第一个不满足AVL条件的节点；本例中，插入点是10，而第一个不满足AVL条件的节点是30；将回溯路径上的节点除节点30外，上移一层，节点30下移一层；

case1


	（这是一个右左双旋转特例，当不符合AVL条件的树根和插入点的父节点只有一个子节点，且相反方向的子节点，当然了，插入点要介于树根和插入点父节点之间的话，才满足双旋转特例的条件）

Attention）

A1）因为10 小于 20 且小于30；所以通过一次单旋转就可以完成；
（也即是，右右单旋转时，不满足AVL条件的最小树的根应该下移，该树的其他节点上移，而不管该树的右子树的左孩子或者存在或不存在，在旋转过程中，都要把该右子树的左孩子添加以作为最小树根的右孩子，因为即使不存在，添加null 也不影响最后的旋转效果）
case2）为什么经过右右单旋转就可以修正成为 AVL 树；因为 new point = 13 不在 4 和 7 之间，所以一次单旋转就可以了，无需双旋转；
（也就是说，new point 介于不满足AVL条件的树根和其孩子之间的话，那么就需要双旋转，否则，只需要单旋转就可以了）

Conclusion of single rotation）单旋转有两个属性：轴和旋转方向

C1）单旋转的轴： 相信你也看到了，单旋转的轴显然是不符合AVL条件的树根的直接孩子；
- C1.1）左左单旋转的轴：是不符合AVL条件的树根的左孩子；
- C1.2）右右单旋转的轴：是不符合AVL条件的树根的右孩子；
C2）旋转方向：
- C2.1）左左单旋转方向：顺时针方向；
- C2.2）右右单旋转方向：逆时针方向；

【3】双旋转

3.1）左右双旋转： （先左左单旋转，再右右单旋转；即先顺时针旋转，后逆时针旋转）

case1）因为47 介于 40 和 50 之间，所以肯定需要双旋转；

3.2）右左双旋转：先将节点15向上提，还是不满足AVL树的条件，再把节点7向上提；（先右右单旋转，再左左单旋转；即先逆时针旋转，后顺时针旋转）
这里写图片描述

Conclusion of double rotations）双旋转有两个属性：轴和旋转方向

C1）双旋转的轴：相信你也看到了，双旋转的轴显然是插入点的直接父节点；（除了两个特例） （干货——双旋转的轴显然是插入点的直接父节点（除了两个特例，而两个特例的轴是插入点本身））
- C1.1）左右单旋转的轴：插入点的父节点；
- C1.2）右左单旋转的轴：插入点的父节点；
C2）旋转方向：
- C2.1）左右单旋转方向：先右右单旋转，再左左单旋转；即先逆时针旋转，再顺时针旋转；
- C2.2）右左单旋转方向：先左左单旋转，再右右单旋转；即先顺时针旋转，再逆时针旋转；

【4】示例图与代码参考

4.1）LL的旋转

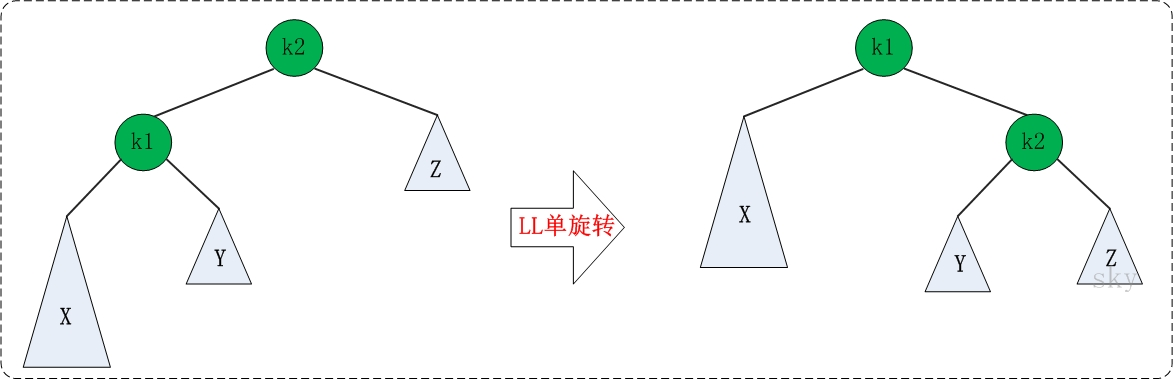
　　图中左边是旋转之前的树，右边是旋转之后的树。从中可以发现，旋转之后的树又变成了AVL树，而且该旋转只需要一次即可完成。　

　　LL的旋转代码：

/*
 * LL：左左对应的情况(左单旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) {
    AVLTreeNode<T> k1;

    k1 = k2.left;
    k2.left = k1.right;
    k1.right = k2;

    k2.height = max( height(k2.left), height(k2.right)) + 1;
    k1.height = max( height(k1.left), k2.height) + 1;

    return k1;
}

　　4.2）RR的旋转

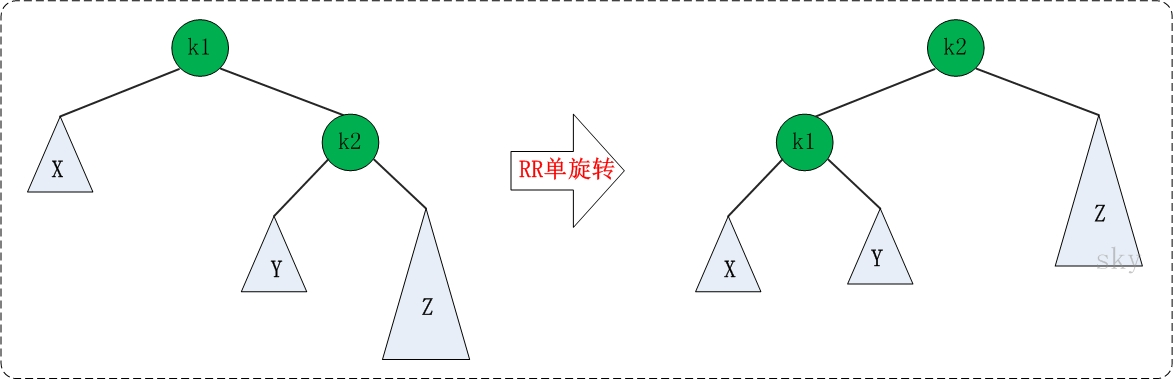
　　图中左边是旋转之前的树，右边是旋转之后的树。RR旋转也只需要一次即可完成。

　　RR的旋转代码：

/*
 * RR：右右对应的情况(右单旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) {
    AVLTreeNode<T> k2;

    k2 = k1.right;
    k1.right = k2.left;
    k2.left = k1;

    k1.height = max( height(k1.left), height(k1.right)) + 1;
    k2.height = max( height(k2.right), k1.height) + 1;

    return k2;
}

　　4.3）LR的旋转

　　第一次旋转是围绕"k1"进行的"RR旋转"，第二次是围绕"k3"进行的"LL旋转"。

　　LR的旋转代码：

/*
 * LR：左右对应的情况(左双旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) {
    k3.left = rightRightRotation(k3.left);

    return leftLeftRotation(k3);
}

　　4.4）RL的旋转

　　第一次旋转是围绕"k3"进行的"LL旋转"，第二次是围绕"k1"进行的"RR旋转"。

　　RL的旋转代码：

/*
 * RL：右左对应的情况(右双旋转)。
 *
 * 返回值：旋转后的根节点
 */
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) {
    k1.right = leftLeftRotation(k1.right);

    return rightRightRotation(k1);
}

　综上，最后的整体插入代码为：

/* 
 * 将结点插入到AVL树中，并返回根节点
 *
 * 参数说明：
 *     tree AVL树的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) {
    if (tree == null) {
        // 新建节点
        tree = new AVLTreeNode<T>(key, null, null);
        if (tree==null) {
            System.out.println("ERROR: create avltree node failed!");
            return null;
        }
    } else {
        int cmp = key.compareTo(tree.key);

           if (cmp < 0) {    // 应该将key插入到"tree的左子树"的情况
            tree.left = insert(tree.left, key);
            // 插入节点后，若AVL树失去平衡，则进行相应的调节。
            if (height(tree.left) - height(tree.right) == 2) {
                if (key.compareTo(tree.left.key) < 0)
                    tree = leftLeftRotation(tree);
                else
                    tree = leftRightRotation(tree);
            }
        } else if (cmp > 0) {    // 应该将key插入到"tree的右子树"的情况
            tree.right = insert(tree.right, key);
            // 插入节点后，若AVL树失去平衡，则进行相应的调节。
            if (height(tree.right) - height(tree.left) == 2) {
                if (key.compareTo(tree.right.key) > 0)
                    tree = rightRightRotation(tree);
                else
                    tree = rightLeftRotation(tree);
            }
        } else {    // cmp==0
            System.out.println("添加失败：不允许添加相同的节点！");
        }
    }

    tree.height = max( height(tree.left), height(tree.right)) + 1;

    return tree;
}

public void insert(T key) {
    mRoot = insert(mRoot, key);
}

posted @ 2017-04-05 19:35 樱の空阅读(13295) 评论(2) 编辑收藏举报

刷新页面返回顶部

樱の空