万物皆对象——第一单元学习小结
一、前言
经过一个月来的学习,我从对面向对象一无所知到逐渐入门,围绕着“多项式求导”,对面向对象的特性进行了探索。
我对面向对象印象最深的两句话就是“万物皆对象”和“高内聚、低耦合”,这三次作业也是尽量贯彻了这两句话。
我们的作业从第一次的仅含幂函数的求导,到第二次包含正余弦函数,再到最后函数可以嵌套。一步步走来,面向对象的优点也逐渐浮现出来。
二、分析工具
本次作业我们用复杂度分析和UML类图对代码进行度量,首先介绍复杂度分析:
复杂度分析是对方法的圈复杂度进行分析,有三个衡量指标:ev(G), iv(G), v(G)
- Cyclomatic Complexity (v(G)) 圈复杂度
- Module Design Complexity (iv(G))模块设计复杂度
模块设计复杂度是用来衡量模块判定结构,即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。
模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度,因此模块设计复杂度不能大于圈复杂度,通常是远小于圈复杂度。
- Essential Complexity (ev(G))基本复杂度
下面我们结合代码对其进行说明:
这是第一次作业打印多项式的一部分,可以看到它的复杂度是

首先我们来看v(G)的计算,画出流程框图,可以看出这个图共有10个点,14条边,则v(G) = 14+2-10 = 6
然后我们来计算iv(G),把没有调用子方法的模块简化成一个点,这段代码中只有for循环里if内部没有调用子方法,因此只有这个if被简化,简化后的图如下
其中有点9个,边12条,iv(G) = 12 + 2 - 9 = 5
最后计算ev(G),我们要把原来流程图结构化的部分简化,这里的结构化的部分指的是只有if/for只有一个入口点,我们代码中的for循环就有两个入口点,因此不能简化(若把原代码的break去掉就可以简化了),具体可以查看Essential complexity - Wikipedia
所作流程图如下,ev(G) = 8 + 2 - 7 = 3
UML类图则是描述类与类之间关系的图,其关系共有继承、实现、依赖、关联、聚合、组合六种,而这三次作业我仅用到了三种依赖,聚合与包含,其他的以后用到了再做总结。
依赖关系是一个类使用了另外一个类。
聚合关系是一个类内部有另外一个类,即has-a关系。
继承关系是一个类继承了另外一个类。
图示:
依赖:
聚合:
继承:![]()
三、代码分析
1. 第一次作业
第一次作业的思路挺清晰的,只知道“万物皆对象”,就把表达式分成一个个项,把表达式抽象成一个对象,把每个项抽象成一个对象,然后用正则表达式去匹配每一项,提取x的指数和系数,然后对对每一项求导并加在表达式对象上,输出就完事了。化简也需要合并同类项,把正项放在第一位,系数为1或-1不输出,指数为1不输出。
圈复杂度:
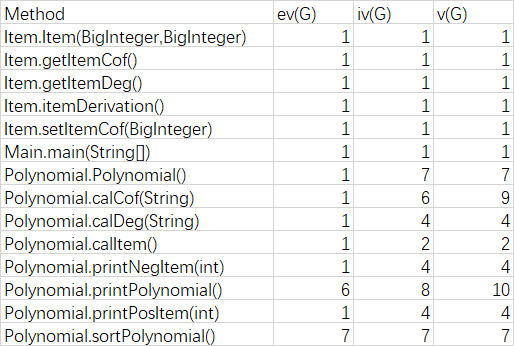
可以看出有几个方法的圈复杂度挺高的,计算指数和系数,打印多项式,因为这几个方法都有很多需要判断系数为不为1,指数为不为1,导致有许多if-else结构。
UML类图:第一次作业还是挺简洁的。
第一次作业算是入门了面向对象了,我努力的运用OO的思想去做这次作业,避免了一main到底的情况,我还学到了正则表达式的使用,java语法结构等。
但是这次作业我出了好几个BUG,1. 没想到他们会用\f来hack,2.合并完同类项忘记删除系数为0的项。
这两个BUG分别出在分析表达式和计算表达式上,都是因为没考虑清楚才导致错误的。
在找BUG阶段,我也使出浑身解数,第一次作业基本就是找WrongFormat大赛,毕竟这次求导太简单了。用各种多符号,少数字的表达式去测试他们,还有合并同类项为0、爆栈的数据,比如:
1231323 + 3131321++32131++661656161
2132*x+- 13213213++2313132*x^3213132
q123213+31321*x
x+x+x+x+x+x+x+x++x++x+-x+- x
313132x^100+x^100+x^99--x^99
3*x^-1+2*x^2
+ + x + + x ++ 2131 * x ^ 2236
321321*x^x
+
-
x^
500个+x
1000个1
x+x-x-x
这次作业相对简单,可以通过阅读代码来构造相应的数据来hack,有一位同学就是用“ | ”作为项与项之间的分隔,然后我构造了一个“|x”的数据他就错了。
2.第二次作业
第二次作业和第一次作业特别相似,仅仅在因子中加入了sin(x),cos(x),其他和第一次作业是一样的,每一项都可以用“a*x^b*sin(x)^c*cos(x)^d”来表示,因此我用了和第一次作业一样的结构而没有去为了兼容第三次而重构代码(主要是懒)。
圈复杂度:
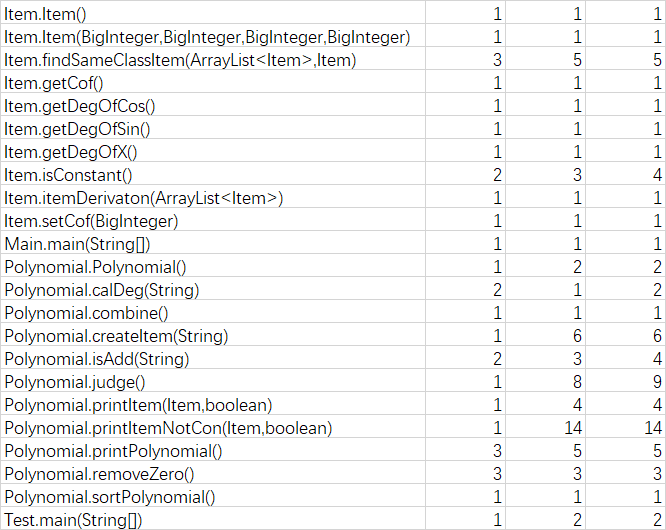
可以看到这次的圈复杂度还是在打印表达式和判断表达式的方法比较高,依旧是那个问题需要判断系数为不为1,指数为不为1,导致有许多if-else结构。
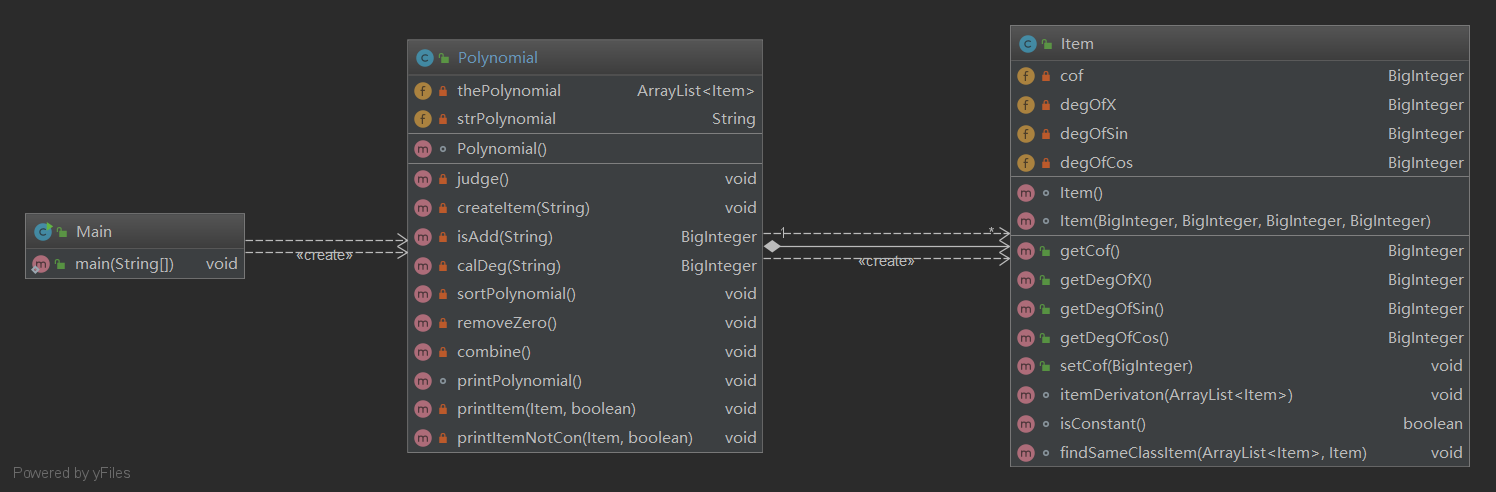
UML类图:和第一次作业差不多
这次的化简主要是运用cos(x)^2+sin(x)^2 = 1这个式子及变式进行化简,用循环找出可以化简的项然后合并就OK。这次作业主要是巩固了一下面向对象的知识点,巩固一下正则表达式的使用,为下一次作业做准备。
这次因为和上次的题目比较像,所以写的挺完善的也没被找出BUG。
找BUG阶段则是阅读别人的代码,然后构造出相应的测试点。
3. 第三次作业
第三次作业的难度陡增,它从表达式的加减乘变成了可以嵌套的模式,这就只能重构代码了,这也揭示了一个问题:前两次作业的代码耦合度过高,难以修改。这次作业的思想主要是把表达式按加减号拆开,得到各个项,再把项按乘号拆开,得到因子,因子有括号,数字,x,sin,cos五种,其中sin,cos,括号可以嵌套表达式,然后递归。
圈复杂度:
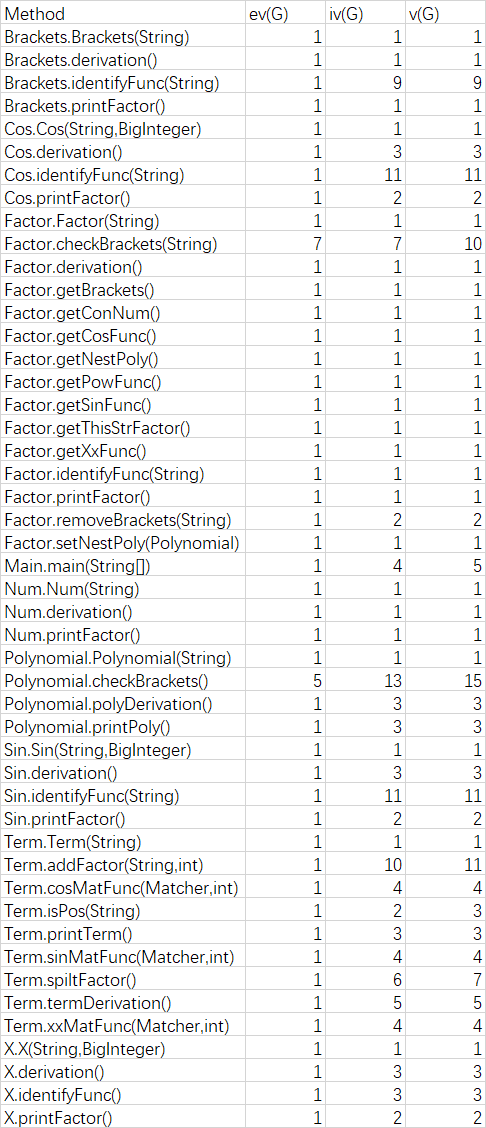
圈复杂度高的依旧是识别函数的方法,这次BUG就出在了识别上。
UML类图:结构比前两次作业复杂了许多
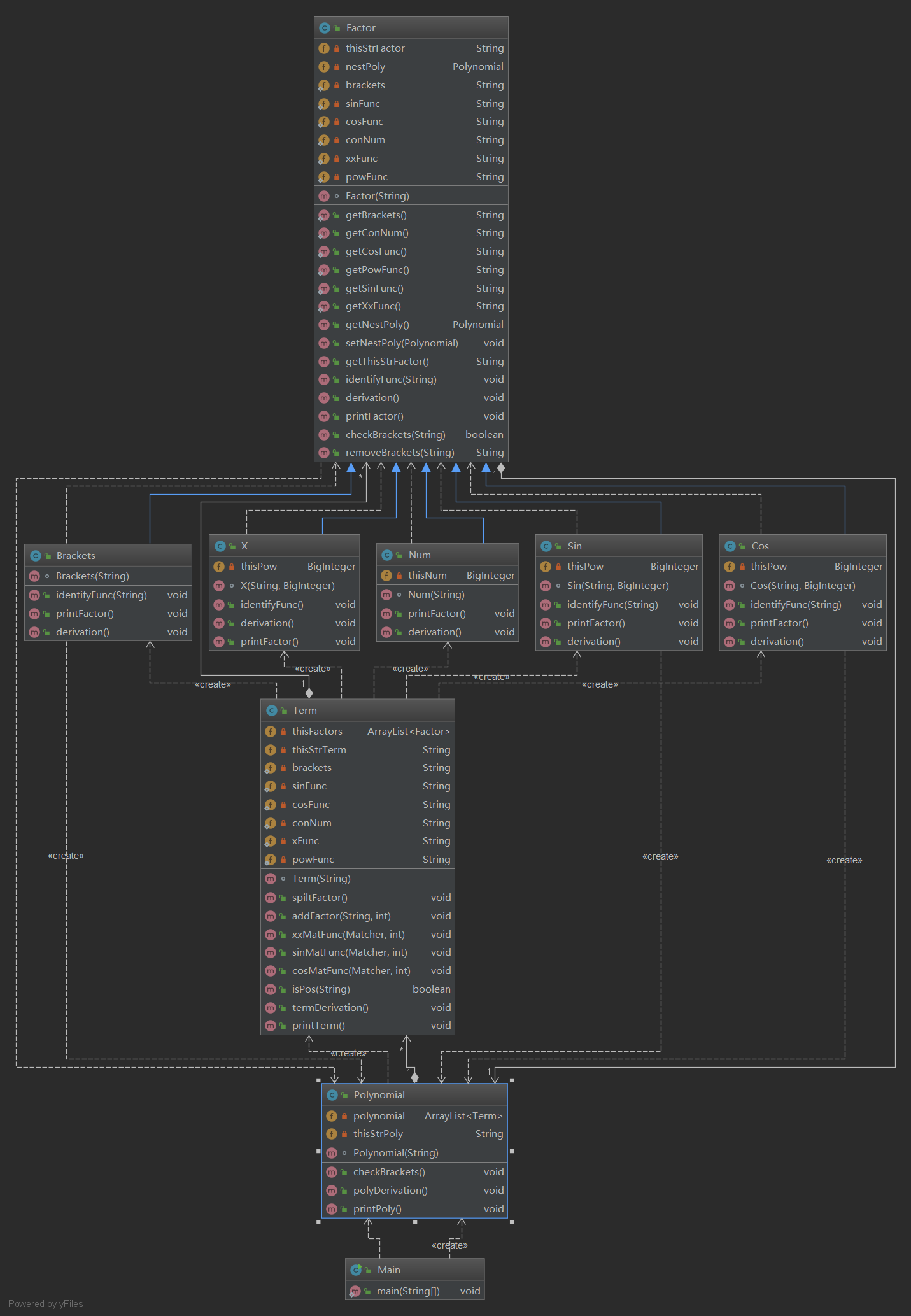
这次作业用到了继承的思想,因子有5种,就用5个子类去继承因子这个父类,这样做的好处也很明显,项是由因子构成的,可以用一个ArrayList<Factor>去存储五种因子,而不要分开存,求导也可以直接调用重写的求导方法Factor.derivation()。本次作业让我对面向对象的理解又深了许多,也复习了一下递归的使用,递归真的好用。
找BUG这次也没什么很好的方法找,只能构建嵌套多层的因子,加各种指数去测试他们的递归会不会有问题,输出会不会有问题。
这次我被找到了一个BUG,就是识别因子的时候,在很多判断中漏了一个条件,导致有些因子识别不出来,会报WF,圈复杂度高果然容易出错。
四、心得体会
几次作业下来对面向对象有一定的了解,知道面向过程与面向对象的区别,明白了“高内聚,低耦合”的道理。在编写代码时,一定先用清晰的思维去构思好程序的设计框架,这样在写代码的时候就不容易因为思绪混乱而写出带BUG的程序。写完程序后要编写完备的测试样例,无论是测试自己的程序还是hack他人的程序都是极好的。
话不多说,继续努力,面向对象,从我做起。
愿诸君共勉!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号