CodeForces - 1243D. 0-1 MST(补图连通分量个数)

Ujan has a lot of useless stuff in his drawers, a considerable part of which are his math notebooks: it is time to sort them out. This time he found an old dusty graph theory notebook with a description of a graph.

It is an undirected weighted graph on 𝑛n vertices. It is a complete graph: each pair of vertices is connected by an edge. The weight of each edge is either 00 or 11; exactly 𝑚m edges have weight 11, and all others have weight 00.

Since Ujan doesn't really want to organize his notes, he decided to find the weight of the minimum spanning tree of the graph. (The weight of a spanning tree is the sum of all its edges.) Can you find the answer for Ujan so he stops procrastinating?

Input

The first line of the input contains two integers 𝑛n and 𝑚m (1≤𝑛≤1051≤n≤105, 0≤𝑚≤min(𝑛(𝑛−1)2,105)0≤m≤min(n(n−1)2,105)), the number of vertices and the number of edges of weight 11 in the graph.

The 𝑖i-th of the next 𝑚m lines contains two integers 𝑎𝑖ai and 𝑏𝑖bi (1≤𝑎𝑖,𝑏𝑖≤𝑛1≤ai,bi≤n, 𝑎𝑖≠𝑏𝑖ai≠bi), the endpoints of the 𝑖i-th edge of weight 11.

It is guaranteed that no edge appears twice in the input.

Output

Output a single integer, the weight of the minimum spanning tree of the graph.

Examples

input

Copy

6 11
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6

output

Copy

2

input

Copy

3 0

output

Copy

0

Note

The graph from the first sample is shown below. Dashed edges have weight 00, other edges have weight 11. One of the minimum spanning trees is highlighted in orange and has total weight 22.

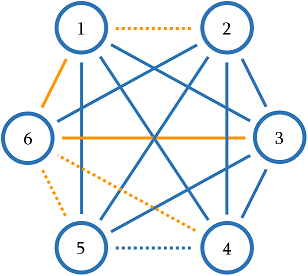
In the second sample, all edges have weight 00 so any spanning tree has total weight 00.

 

题意:完全图,给出一部分,求补图连通分量个数.

答案为连通分量个数减1, 用bitset优化太巧妙了~~~

对于每一个点(没有被访问过),枚举不和它相连并且没有访问过的点,依次dfs下去,得到一个连通分量.

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010;
map<int,bool>mp[maxn];
bitset<maxn>bit;
void dfs(int u){
    bit[u] = 0;
    for(int i = bit._Find_first();i < bit.size();i = bit._Find_next(i)){
        if(!mp[u][i])dfs(i);
    }
}
int main()
{
    int n,m;
    cin >> n >> m;
    for(int i = 1;i <= m;i++){
        int u,v;
        cin >> u >> v;
        mp[u][v] = mp[v][u] = 1;
    }
    for(int i = 1;i <= n;i++)bit[i] = 1;
    int sum = 0;
    for(int i = 1;i <= n;i++){
        if(bit[i])dfs(i),sum++;
    }
    cout << sum - 1 << endl;
    return 0;
}