Square Tree
作者:@cherish.
课程学习内容为作者从学校的PPT处摘抄,仅供自己学习参考,若需转载请注明出处:https://www.cnblogs.com/cherish-/p/16538416.html
Square Tree
题目链接: [Square Tree](SquareTree (nowcoder.com))
题目描述:给你一棵个节点的树,根节点为。初始时所有结点的权值都为。给你次操作,每次操作给你三个数,其含义为:若节点,其子树中含从到的路径中的节点,则将节点的权值乘以。次操作后,给个询问,每个询问给定一个节点编号,若节点的权值是完全平方数,则输出YES,否则输出NO。
数据范围:。
思路:首先不管树上操作,先来看如何判断是否为完全平方数,显然要判断其表示成质因数乘积的形式的时候,其所有质因数的幂次是否为偶数,若是,则YES,否则NO。考虑到,所以我们可以将所有质因数求出来,重新编号,进行状压,因为只需要考虑奇偶性,所以乘法就变成异或运算。再来看操作是怎样完成的。
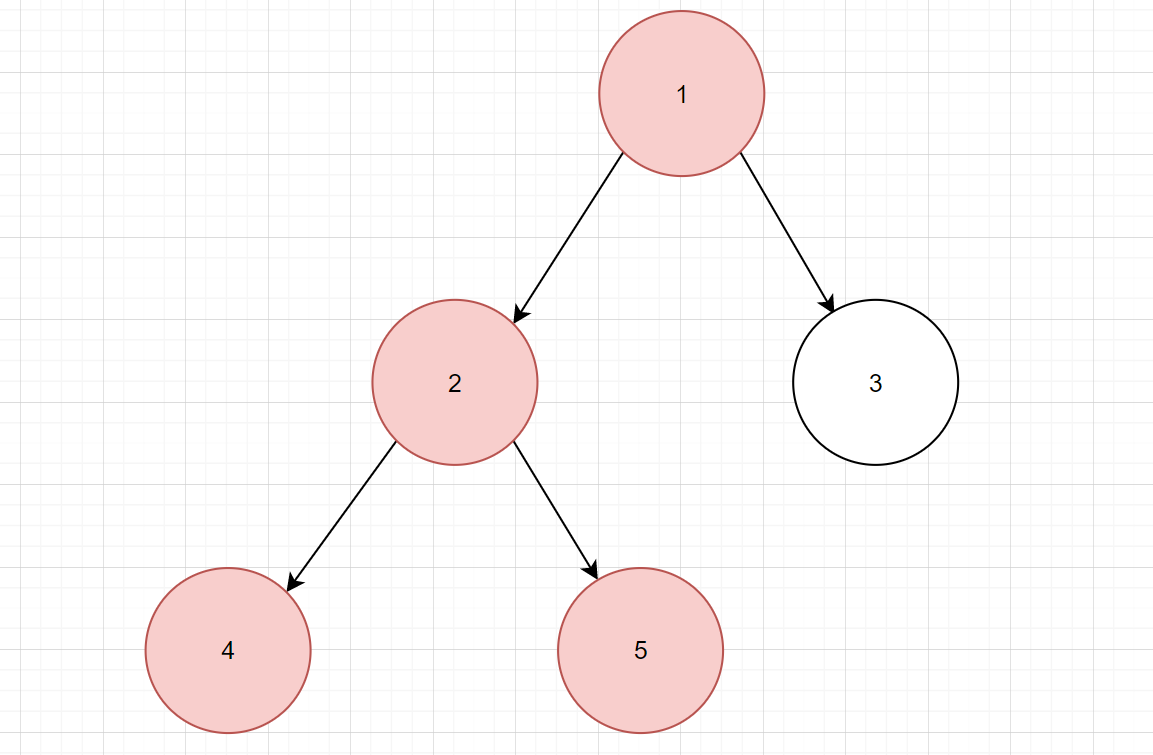
对于如图所示的一棵树,假设当前给定的操作的,那么显然要更新两条路径:和但不包括。但考虑到判断平方数,对一个数乘同一个数三次和乘一次,其是否为平方数的性质不会发生改变,所以实际要对 , ,这三条路径上的点都乘以权值,也即都与转化后的权值进行异或运算。在询问的时候,我们只需要查询该点最终值是否为即可。对于树上链的更新,是比较明显的树链剖分。
时间复杂度:
参考代码:
#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;
using ll = long long;
struct segmentTree {
int lr, rs, mid;
ll tag;
};
const int N = 2e5 + 5;
segmentTree tree[N << 2];
unordered_map<int, int>mp;
vector<int>pri;
void pushDown(int rt) {
if (tree[rt].tag == 0) return;
tree[rt << 1].tag ^= tree[rt].tag;
tree[rt << 1 | 1].tag ^= tree[rt].tag;
tree[rt].tag = 0;
return;
}
void buildTree(int rt, int lr, int rs) {
tree[rt].lr = lr; tree[rt].rs = rs;
if (lr == rs) return;
int mid = tree[rt].mid = lr + rs >> 1;
buildTree(rt << 1, lr, mid);
buildTree(rt << 1 | 1, mid + 1, rs);
return;
}
void update(int rt, int lr, int rs, ll val) {
if (tree[rt].lr > rs || tree[rt].rs < lr) return;
if (tree[rt].lr >= lr && tree[rt].rs <= rs) {
tree[rt].tag ^= val;
return;
}
pushDown(rt);
if (tree[rt].mid >= lr) update(rt << 1, lr, rs, val);
if (tree[rt].mid < rs) update(rt << 1 | 1, lr, rs, val);
return;
}
bool query(int rt, int pos) {
if (tree[rt].lr > pos || tree[rt].rs < pos) return false;
if (tree[rt].lr == tree[rt].rs) return tree[rt].tag == 0;
pushDown(rt);
if (tree[rt].mid >= pos) return query(rt << 1, pos);
return query(rt << 1 | 1, pos);
}
ll query1(int rt, int pos) {
if (tree[rt].lr > pos || tree[rt].rs < pos) return -1;
if (tree[rt].lr == tree[rt].rs) return tree[rt].tag;
pushDown(rt);
if (tree[rt].mid >= pos) return query(rt << 1, pos);
return query(rt << 1 | 1, pos);
}
bool check(int x) {
if (x == 2) return true;
if (x % 2 == 0) return false;
for (int i = 3; i * i <= x; i += 2) {
if (x % i == 0) return false;
}
return true;
}
int cnt = 0;
void init() {
for (int i = 2; i <= 100; ++i) {
if (!check(i)) continue;
mp[i] = cnt++;
pri.push_back(i);
}
}
vector<vector<int>>graph(N);
int a[N];
int father[N], depth[N], siz[N], son[N];
void dfs1(int u, int f) {
father[u] = f; depth[u] = depth[f] + 1;
siz[u] = 1;
int maxsize = -1;
for (auto g : graph[u]) {
if (g == f) continue;
dfs1(g, u);
siz[u] += siz[g];
if (siz[g] > maxsize) maxsize = siz[g], son[u] = g;
}
return;
}
int tim, dfn[N], top[N], outtime[N];
void dfs2(int u, int t) {
dfn[u] = ++tim;
top[u] = t;
if (!son[u]) return;
dfs2(son[u], t);
for (auto g : graph[u]) {
if (g == father[u] || g == son[u]) continue;
dfs2(g, g);
}
outtime[u] = tim;
return;
}
void updateChain(int u, int v, ll val) {
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]]) swap(u, v);
update(1, dfn[top[u]], dfn[u], val);
u = father[top[u]];
}
if (depth[u] > depth[v]) swap(u, v);
update(1, dfn[u], dfn[v], val);
return;
}
int f[N][20], dep[N];
void dfs(int u, int fa) {
f[u][0] = fa;
dep[u] = dep[fa] + 1;
for (int i = 1; (1 << i) <= dep[u]; ++i) f[u][i] = f[f[u][i - 1]][i - 1];
for (auto v : graph[u]) {
if (v == fa) continue;
dfs(v, u);
}
return;
}
int LCA(int u, int v) {
if (dep[u] > dep[v]) swap(u, v);
for (int i = 18; ~i; --i)
if (dep[f[v][i]] >= dep[u]) v = f[v][i];
if (u == v) return u;
for (int i = 18; ~i; --i) {
if (f[u][i] != f[v][i]) {
u = f[u][i];
v = f[v][i];
}
}
return f[u][0];
}
void solve() {
init();
int n, m, q;
cin >> n;
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(1, 1);
dfs1(1, 1);
dfs2(1, 1);
buildTree(1, 1, n);
cin >> m;
auto cal = [&](int w) {
ll res = 0;
for (auto p : pri) {
if (w % p != 0) continue;
int cnt = 0;
while (w % p == 0) cnt++, w /= p;
if (cnt % 2) res |= (1ll << mp[p]);
if (w == 1) break;
}
return res;
};
for (int i = 1; i <= m; ++i) {
int a, b, w;
cin >> a >> b >> w;
ll val = cal(w);
int p = LCA(a, b);
updateChain(a, b, val);
updateChain(1, p, val);
updateChain(p, p, val);
}
cin >> q;
while (q--) {
int x;
cin >> x;
if (query(1, dfn[x])) cout << "YES" << '\n';
else cout << "NO" << '\n';
}
//for (int i = 1; i <= n; ++i) cout << query1(1, dfn[i]) << " ";
return;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T = 1;
//cin >> T;
while (T--) solve();
return 0;
}
作者:cherish.
出处:https://home.cnblogs.com/u/cherish-/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!