第六章 LR分析

作者：@cherish.
课程学习内容为作者从学校的PPT处摘抄，仅供自己学习参考，若需转载请注明出处：https://www.cnblogs.com/cherish-/p/16382392.html

---

LR分析

LR分析概述

• LR(k):L(Left to right parsing)，R(right-most derivation in reverse)，K(look ahead k token(s))；

• 移进-归约法（shift-reduce)；

• 框架：总控程序、分析栈和分析表三个组成部分

  

【例】

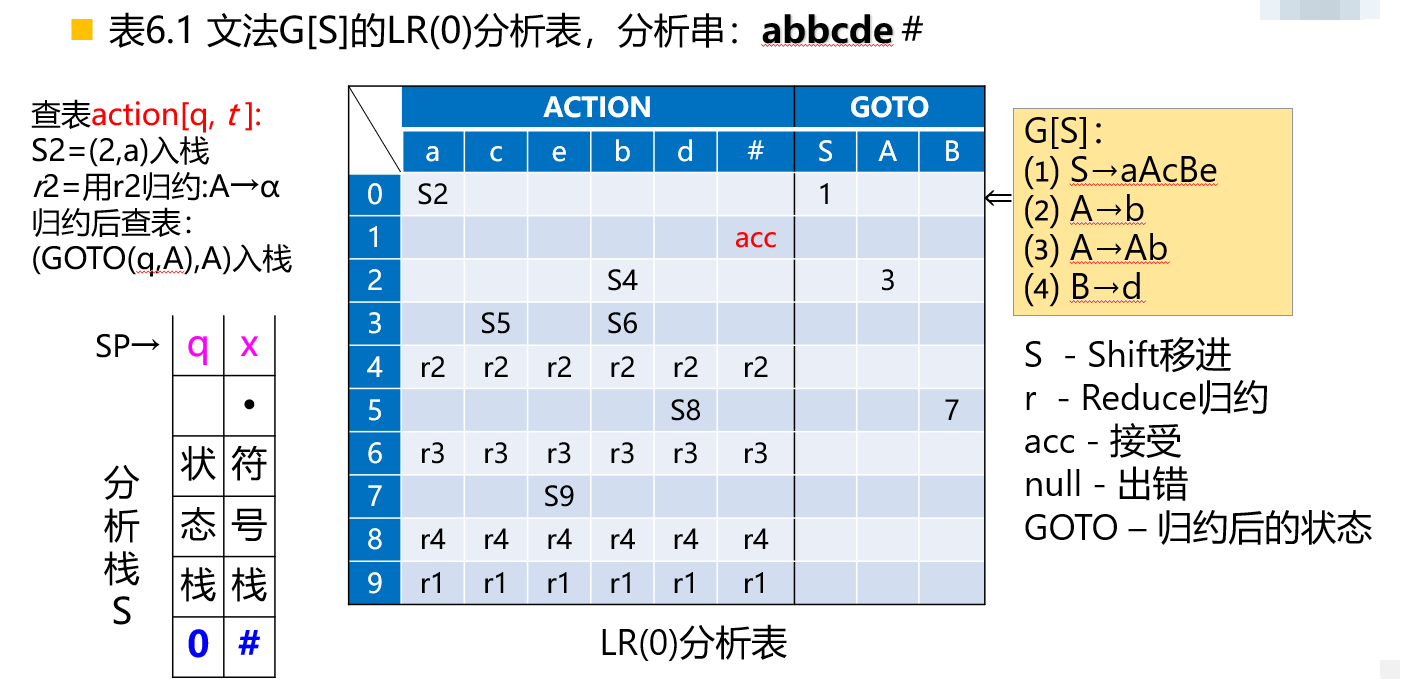
假设文法$G[S]$和分析表$M$，状态$(0 , \#)$为开始状态，$(q , a)$为栈顶元素（q为状态，a为输入符号），则总控程序的算法如下：

• 初始化：$(0 ,\#)$进栈$S$；

• 读下一个输入符号$a$，根据ACTION(q , a)的值执行不同动作；

  • 移进：$if(ACTION[q , a] == S_j)$，则$(j , a)$入分析栈$S$；

  • 归约：$if(ACTION[q , a] == r_i)$，采用规则$i$归约；

    • 设规则$i$为$A \to \alpha$，将$|\alpha|$个状态和符号弹出分析栈$S$；

    • $if(GOTO[q , A] == null) ERR()$;

      $else(GOTO[q , A] , A)$入分析栈$S$。

  • 报错：$if(ACTION[q , a] == null) ERR()$；

  • 接受：$if(ACTION[q , a] == acc)$接受并结束。

  • 反复执行移进-归约，直到接受或报错。

【例】

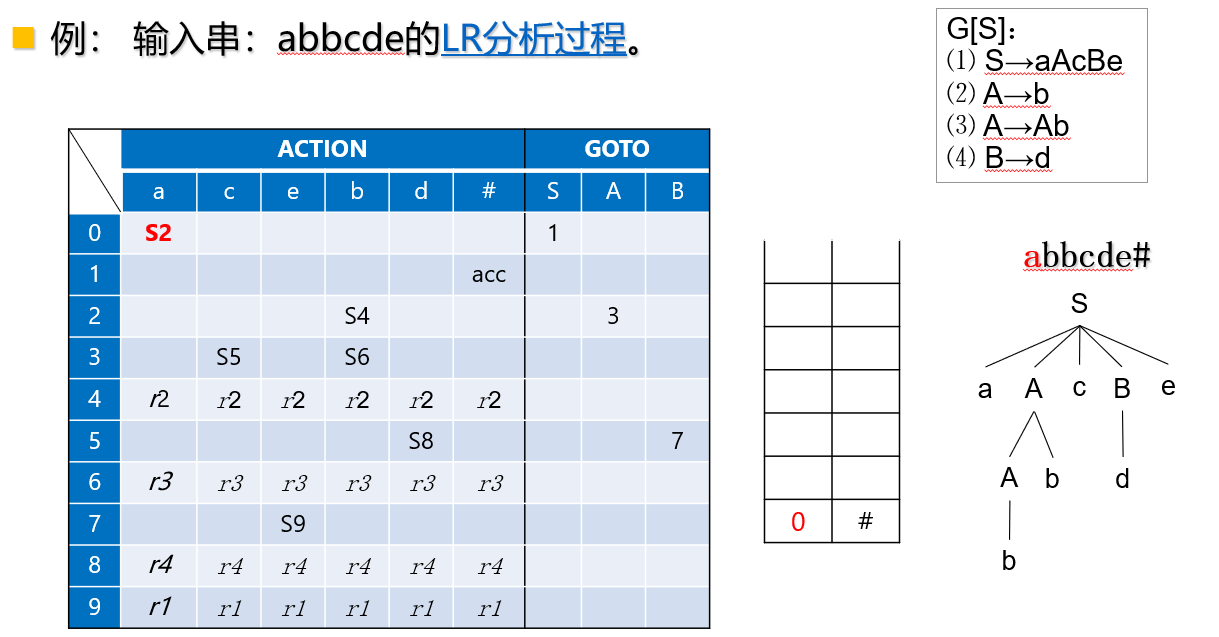
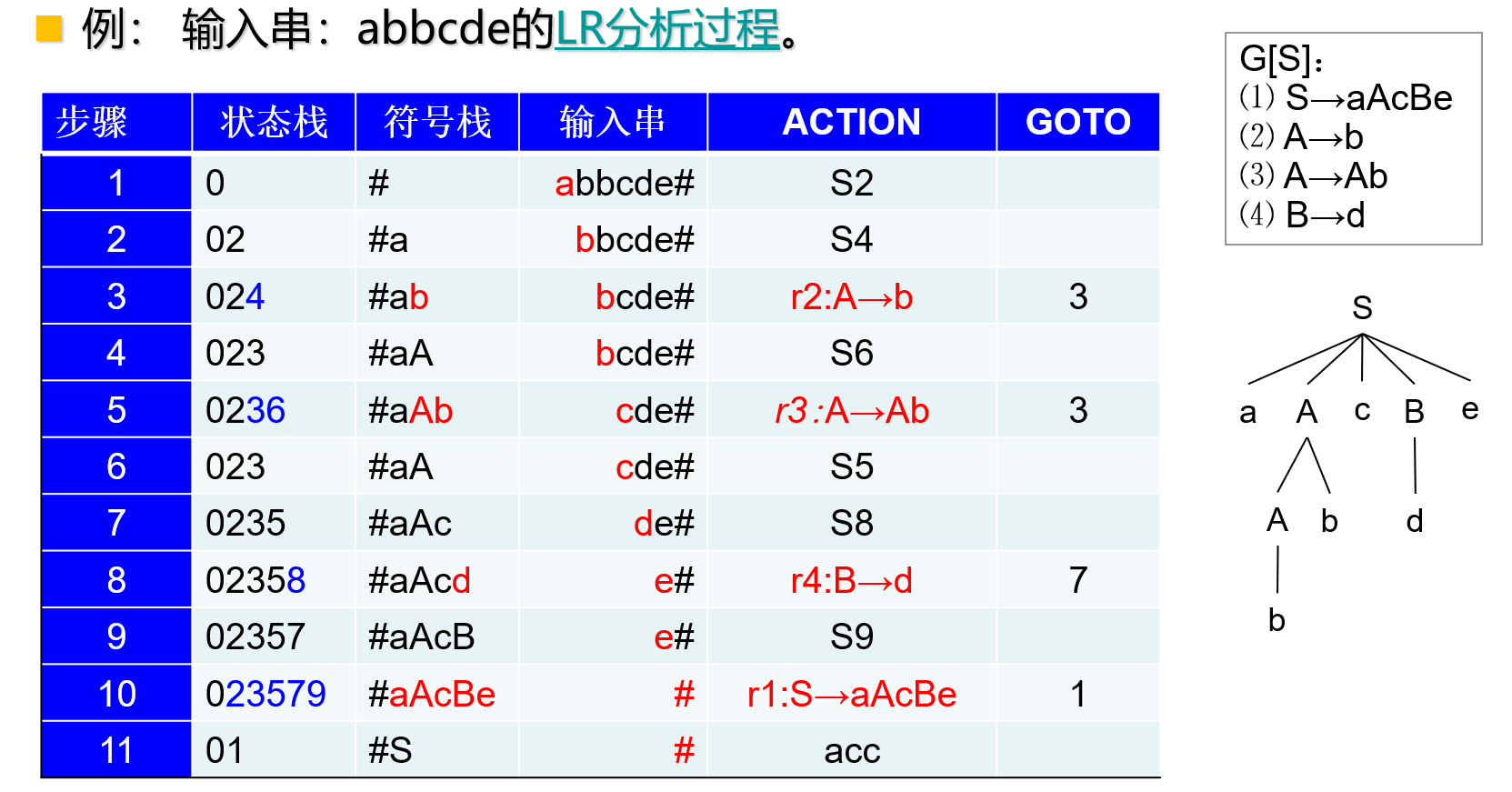
LR(0)分析

定义：将符号串的任意含有头符号的子串称为前缀。特别地，空串$\varepsilon$为任意串的前缀。

定义：设文法$G[S]$，如果$S \stackrel{*}{\Rightarrow} \alpha A \omega \Rightarrow \alpha \beta \omega$是句型$\alpha \beta \omega$的规范推导，则$\alpha \beta$称为可归前缀，$\alpha \beta$的前缀称为活前缀。

【例】

识别活前缀DFA技术路线是根据文法$G$，构造识别活前缀NFA M。之后通过子集法，将NFA M确定化，得到识别活前缀DFA M。

识别$G = (V_N , V_T , P ,S)$活前缀的NFA：

• 文法$G$等价改写成$G'$：文法$G' = (V_N \cup \{S'\} , V_T , P \cup \{S' \to S\} , S')$；$V_N \cap \{S'\} = \empty$；

• 每个规则$A \to \alpha$构造等价一个$NFAMA \to \alpha$：

  令$\alpha = x_1x_2...x_n$，增加$n + 1$个状态$q_1 , q_2 , ... , q _ {n + 1}$；

  $f(q_i , x_i) = \{q_{i + 1}\} (1 \leq i \leq n)$，$q_1$为开始状态，$q_{n + 1}$为结束状态，$\sum = \{x_1 , x_2 , ... , x_n\}$；

• 合并所有规则的$NFAM \to \alpha$，构造成一个NFA M：

  如果$M_A \to \alpha$有$f(q , B) = \{p\}, B \in V_N$，且$NFA\;B_B\to \beta$对应开始状态为$q'$，增加转换$f(q , \varepsilon) \supseteq \{q'\}$；最后仅保留$NFA\;M_{S'} \to S$的开始状态为NFA M的开始状态。

【例】

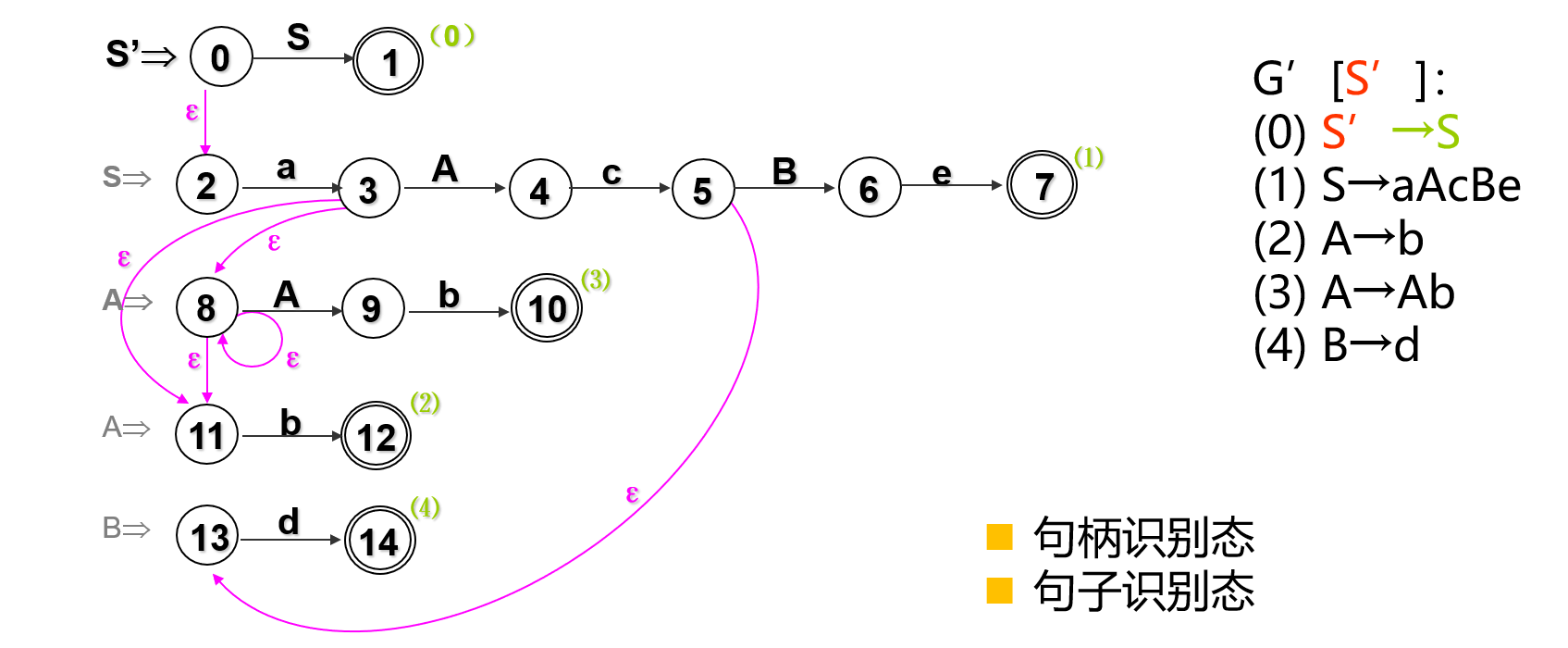
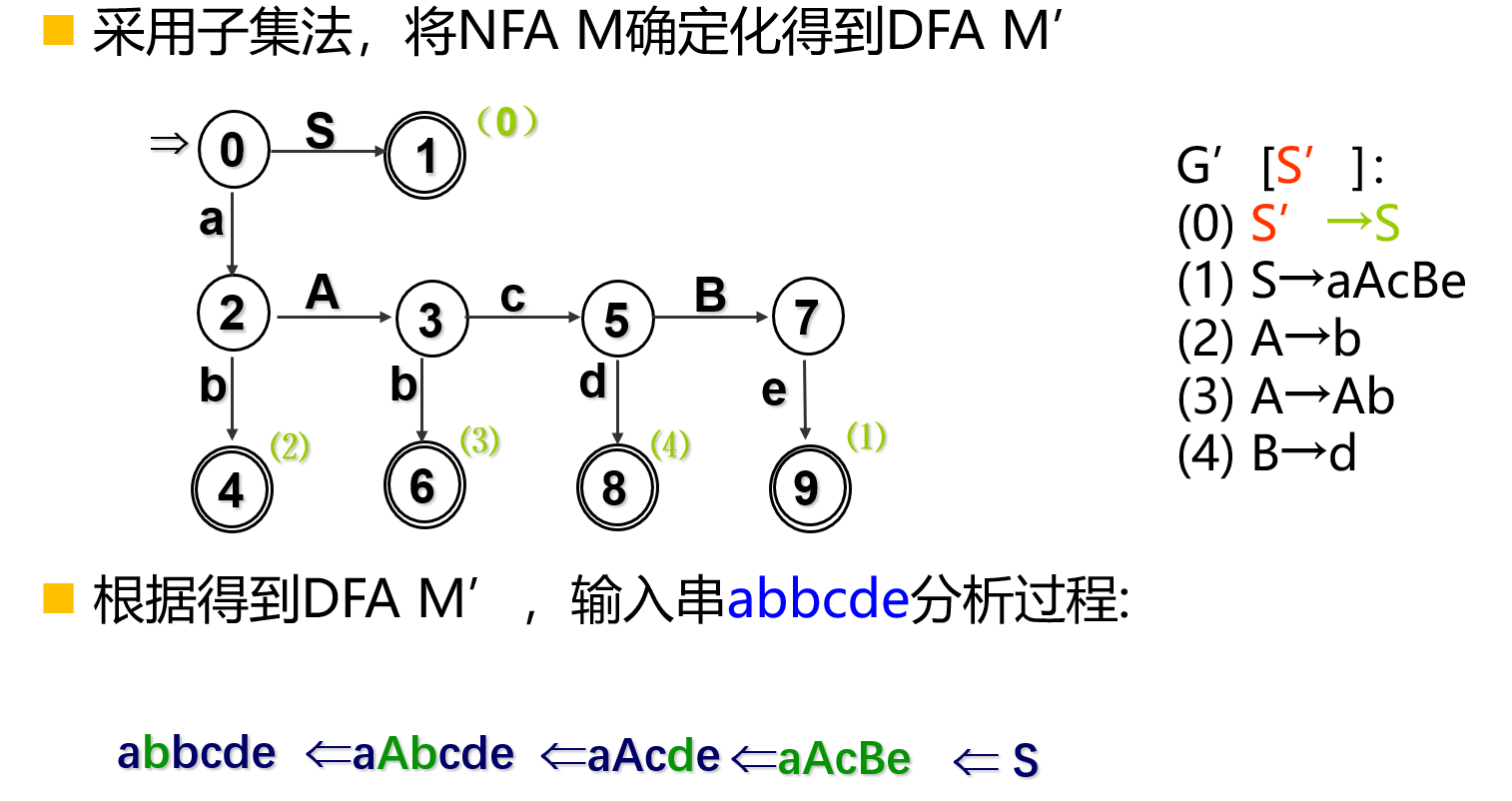
$M(A \to \alpha)$的状态可以直接由$A \to \alpha$规则来命名，对于规则：$A \to \alpha \beta \gamma$有：

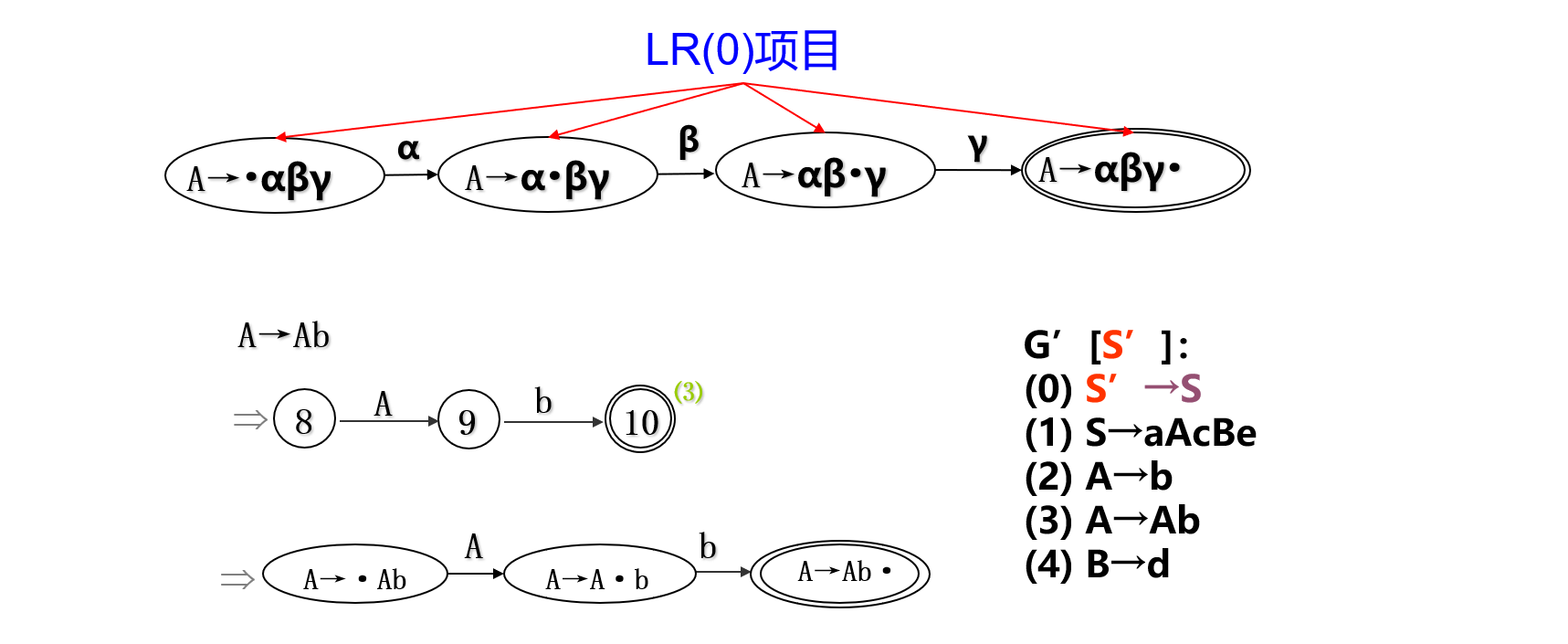
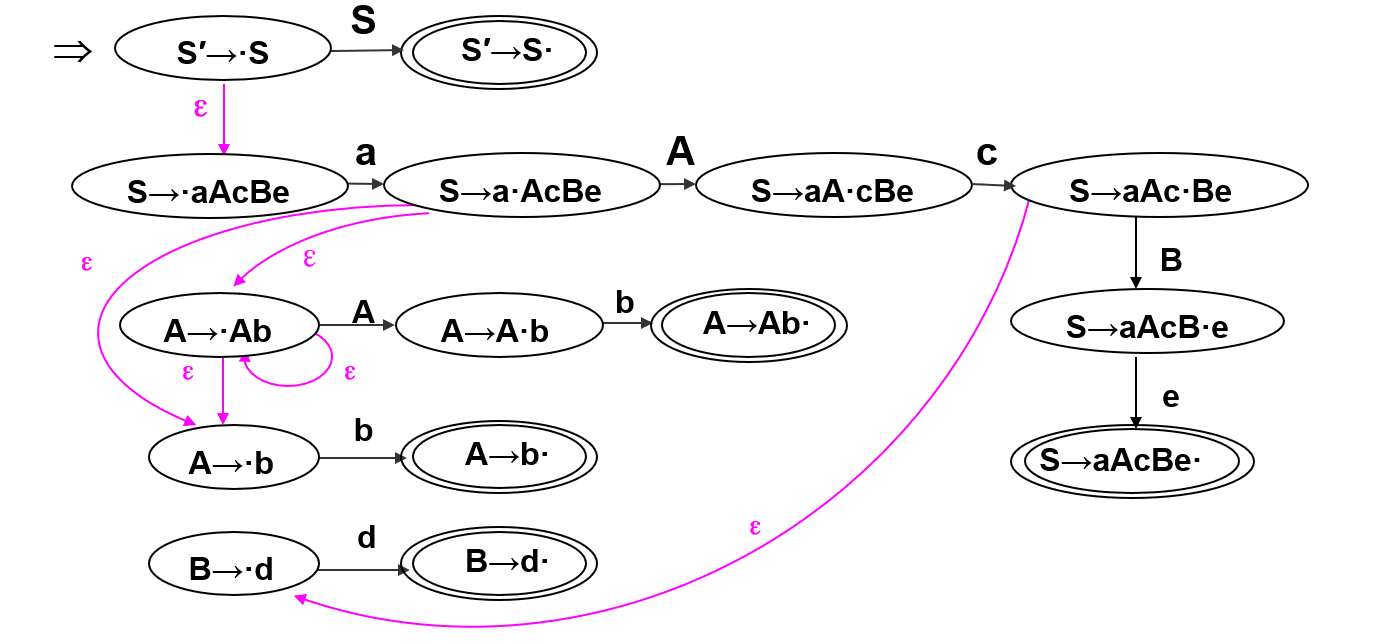
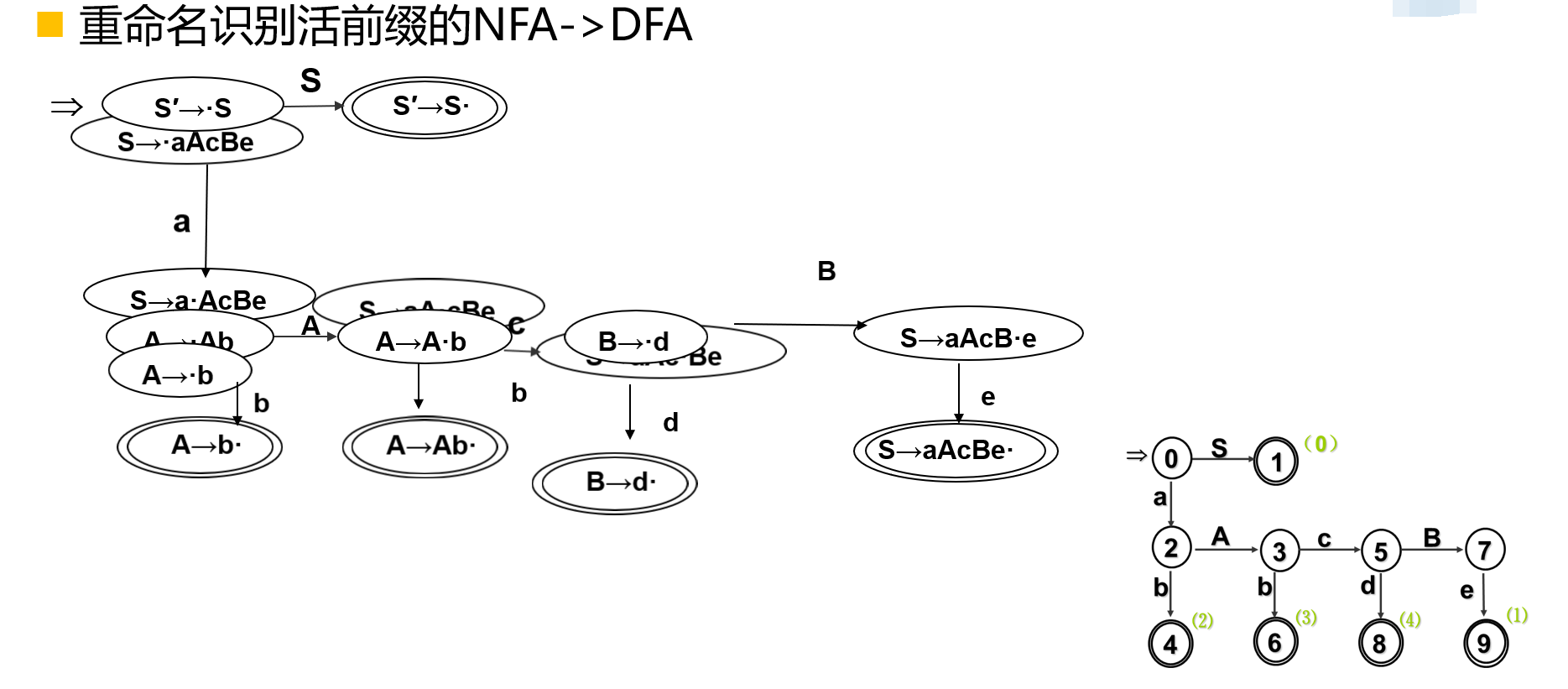
通过LR(0)项目集（规范族）直接构造识别活前缀的DFA：

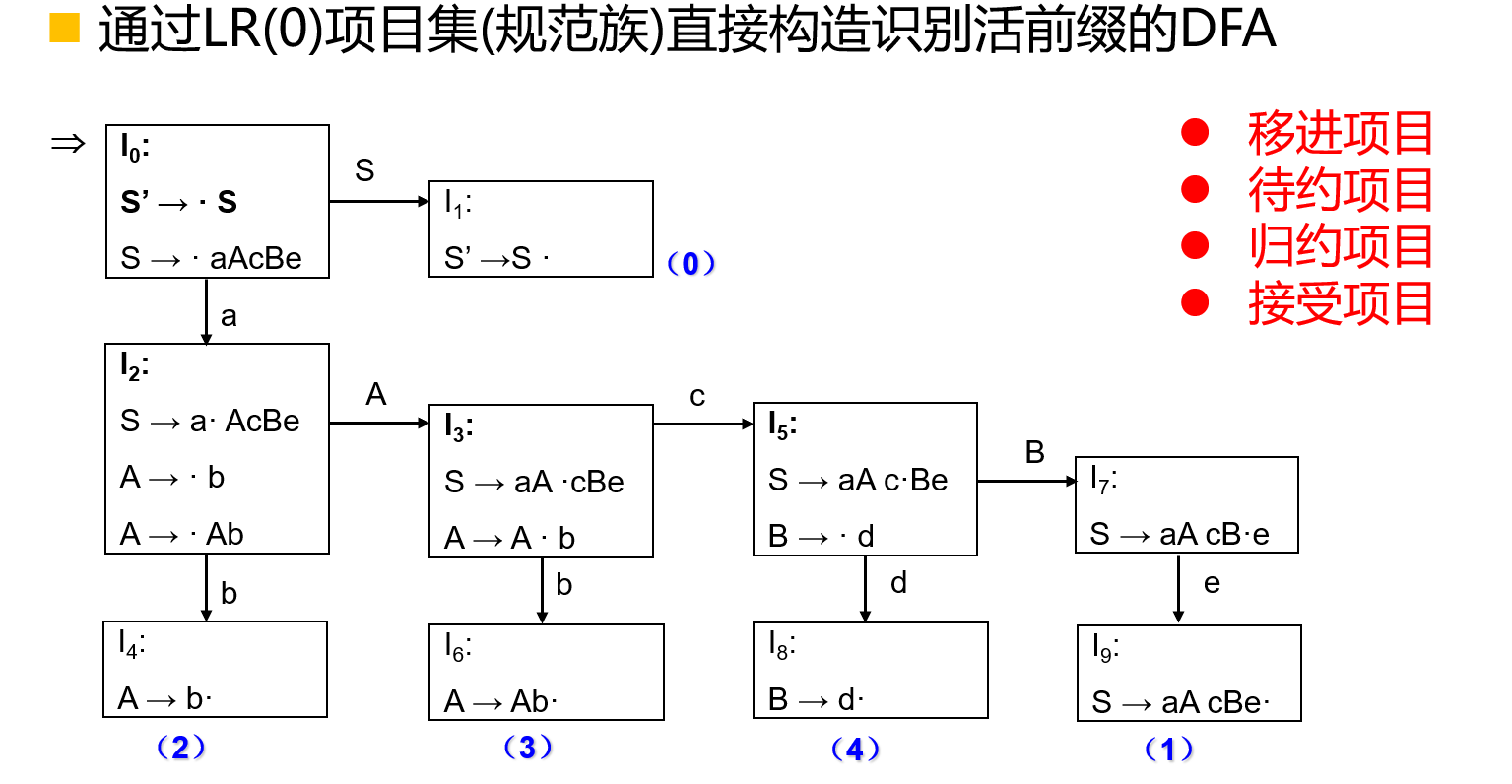
LR(0)项目的分类：

• 移进项目：$A \to \alpha \cdot a \beta$；
• 待约项目：$A \to \alpha \cdot X \beta$；
• 归约项目：$A \to \alpha \cdot$；
• 接受项目：$S' \to \alpha \cdot$；
• 其中$\alpha , \beta \in (V_N \cup V_T)^* , a \in V_T , X \in V_N$；
• 特别地，空规则$A \to \varepsilon$对应LR(0)项目为$A \to \cdot$。

$DFA \to LR(0)$分析表：

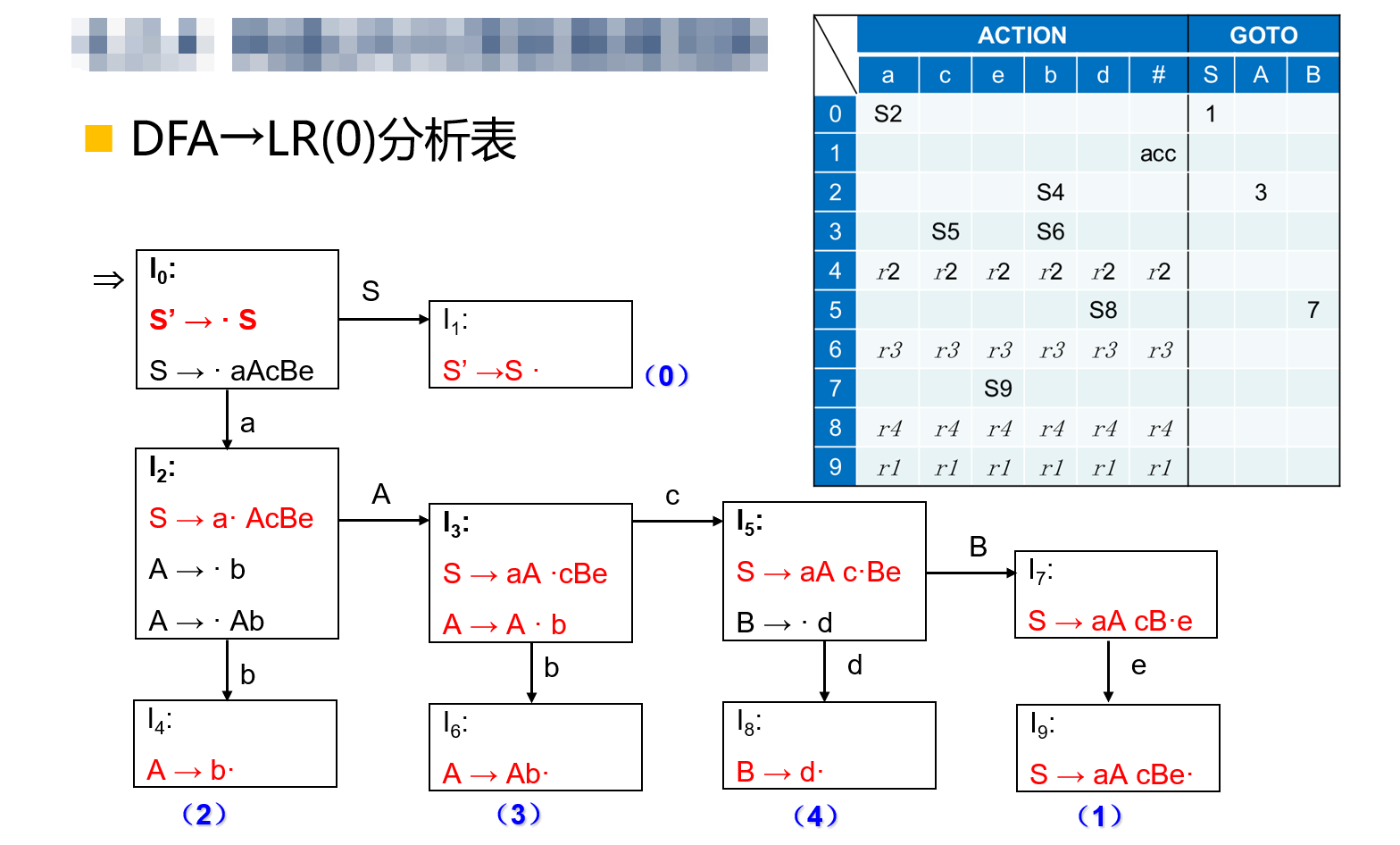
LR(0)项目的MOVE运算定义

定义：设$I$是文法$G$的LR(0)项目子集，则$MOVE(I , X)$定义如下：

$$MOVE(I , X) =\{A \to \alpha X \cdot \beta | A \to \alpha \cdot X \beta \in I \}$$

【例】

$I = \{S \to a \cdot AcBe , A \to \cdot A b , A \to \cdot b\}$；

$MOVE(I , A) = \{S \to aA \cdot cBe , A \to A \cdot b\}$；

$MOVE(I , b) = {A \to b \cdot}$。

LR(0)项目的CLOSURE运算

定义：设$I$是文法$G$的LR(0)项目子集，则closure(I)定义如下：

• $I \sub closure(I)$；
• $\{B \to \cdot \gamma | A \to \alpha \cdot B \beta \in closure(I)\} \sub closure(I)$；
• 重复上一步，直到closure(I)不再扩大为止。

【例】

$I = \{S \to a \cdot AcBe\}$；

则$closure(I) = \{S \to a \cdot AcBe , A \to \cdot Ab , A \to \cdot b\}$；

LR(0)识别活前缀DFA M构造方法

设文法$G = (V_N , V_T , P , S)$，且已等价改写成文法$G'$，即$G' = (V_N \cup \{S'\} , V_T , P \cup \{S' \to S\} , S')$；$V_N \cap \{S'\} = \empty$；则识别活前缀$DFA\;M = (K , \sum , f , S , Z)$，其中：

• $K \subseteq p$，（$LR(0)$项目集）;
• $\sum = V_N \cup V_T$；
• $f(I , X) = closure(MOVE(I , X)) , I \in K , X \in \sum$；
• $S = closure(S' \to S)$；
• $Z = \{q | q \in K , q含有归约项目\}$;

定义：文法$G$的识别活前缀$DFA\;M$的状态集称为文法$G$的$LR(0)$项目集规范族。

【例】

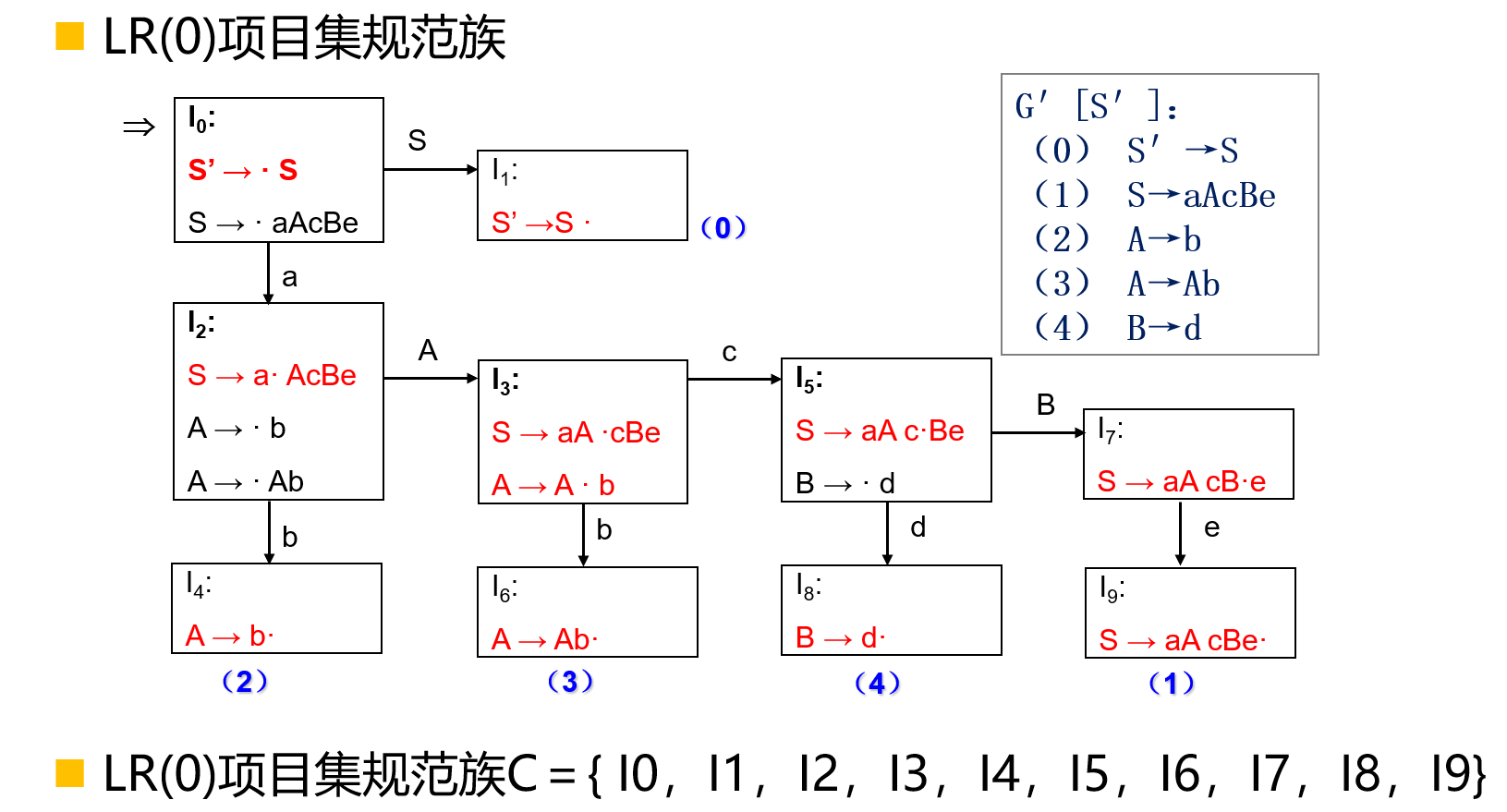
LR(0)分析表的构造

设文法$G$的$LR(0)$项目集规范族$C =\{I_0 , I_1 , ...,I_n\}$，且$f$为转换函数，则对每一个$LR(0)$项目，依据下列情况分别填分析表：

• 如果移进项目$A \to \alpha \cdot a \beta \in I_k , f(I_k , a) = I_j$，则置$ACTION[k , a] = S_j$；
• 如果归约项目$A \to \alpha \cdot \in I_k , A \to \alpha$标号为$i$，$\forall\;a \in (V_T \cup \{\#\})$，置$ACTION[k , a] = r_i$；
• 如果接受项目$S' \to S\cdot \in I_k$，则置$ACTION[k , \#] = acc$；
• 如果$f(I_k , A) = I_i , A \in V_N$，则置$GOTO[k , A] = j$；

凡按上述过程没能填入分析表元素$ACTION[k , a]$和$GOTO[k , a]$置为$e_t$，$t$为错误编号。

【例】

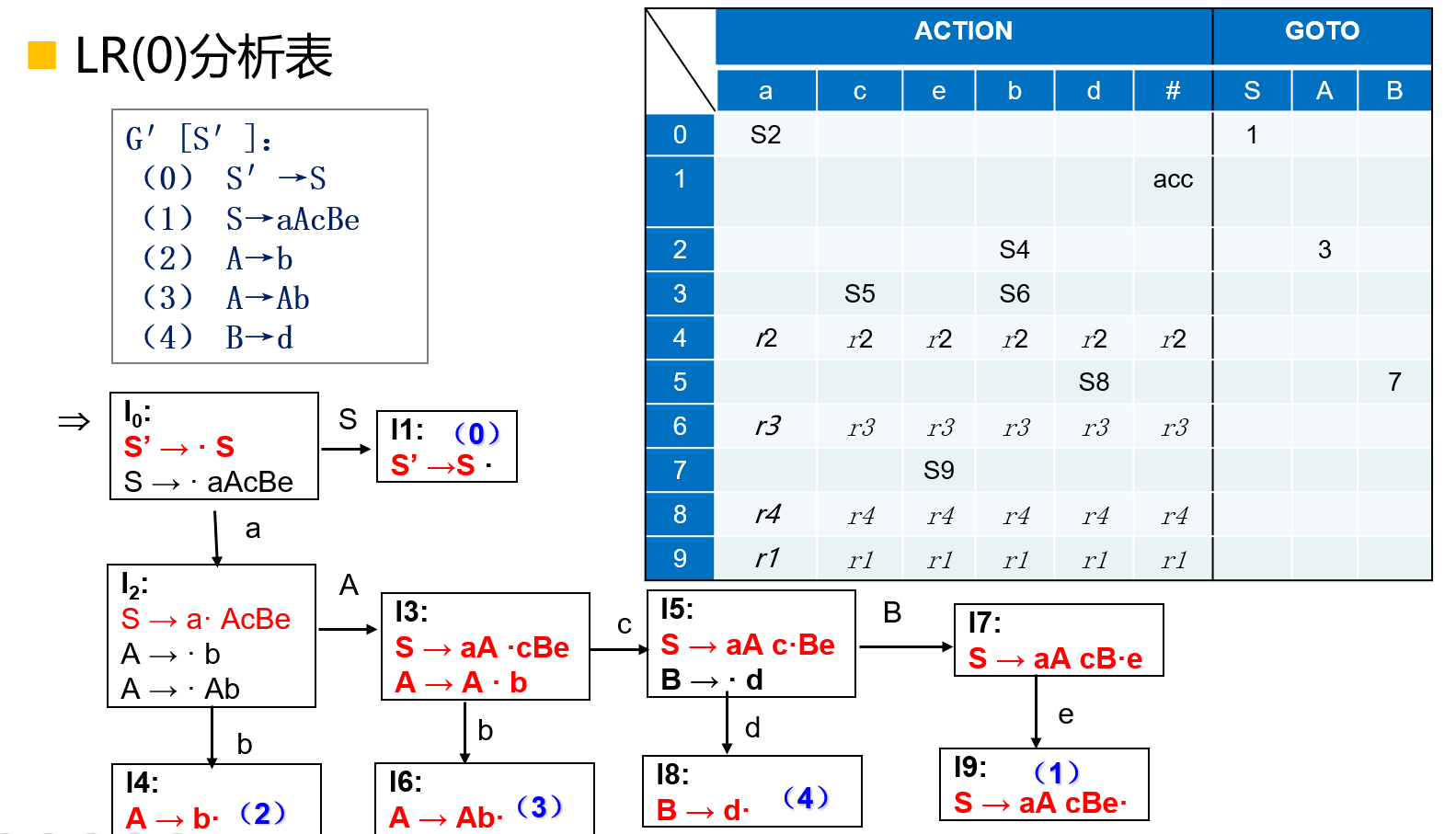
移进-归约冲突：项目集中同时出现移进和归约项目如$A \to \alpha \cdot a \beta , B \to \gamma \cdot$；

归约-归约冲突：项目集中同时出现多个归约项目如$A \to \alpha \cdot , B \to \beta \cdot$；

定义：如果文法$G$的$LR(0)$项目集规范族不存在移进-归约冲突或归约-归约冲突的项目集，则文法$G$称为$LR(0)$文法。

• 如果文法$G$是$LR(0)$文法，则$G$可采用$LR(0)$分析法。
• 如果文法$G$是$LR(0)$文法，则$G$是无二义性的。
• $LR(0)$分析表ACTION表中每格仅会是移进、归约和报错$3$种动作之一。

SLR(1)分析

不是$LR(0)$文法时，可以采用简单地向后看$1$个输入符号的方法，解决移进-归约冲突或归约-归约冲突。

假设文法$LR(0)$项目集规范族有一个并存移进-归约或归约-归约冲突的项目集$I_k = \{A \to \alpha \cdot a \beta , A \to \gamma \cdot , B \to \delta \cdot , ...\}$；若$\{a\} \cap FOLLOW(A) \cap FOLLOW(B) = \empty$则冲突可解决:

• 如果下一个符号$a_i \in 移入符号集$，移入；
• 如果下一个符号$a_i \in FOLLOW(A)$，用$A \to \gamma$归约；
• 如果下一个符号$a_i \in FOLLOW(B)$，用$B \to \delta$归约。

这种分析方法称为SLR(1)分析法。

SLR(1)分析表的构造

对每一个$LR(0)$项目，依据下列情况分别填分析表：

• 如果移进项目$A \to \alpha \cdot a \beta \in I_k , f(I_k , a) = I_j$，则置$ACTION[k , a] = S_j$；
• 如果归约项目$A \to \alpha \cdot \in I_k , A \to \alpha$标号为$i$，$\forall \;a \in FOLLOW(A)$，则置$ACTION[k , a] = r_i$；
• 如果接受项目$S' \to S\cdot \in I_k$，则置$ACTION[k , \#] = acc$；
• 如果$f(I_k , A) = I_j , A \in V_N$，则置$GOTO[k , A] = j$；

凡按上述步骤没能填入分析表元素$ACTION[k , a]$和$GOTO[k , a]$，置为$e_t$，$t$为错误编号。

定义：设文法$G$的$LR(0)$项目集规范族$C$中任意含有$m$个移进项目和$n$个归约项目的冲突项目集$I_k$的一般形式为：$I_k = \{A_1 \to \alpha_1 \cdot a_1 \beta_1, ... ,A_m \to \alpha_m \cdot a_m \beta_m , B_1 \to \gamma_1 \cdot ,... , B_n \to \gamma_n \cdot , ...\}$；其中$A_i , B_j \in V_N , a_i \in V_T , \alpha_i , \beta_j , \gamma_q \in (V_N \cup V_T)^* , ...$表示剩下的待约项目。

如果移进符号集${a_1 , a_2 , ... , \alpha_m}$和$FOLLOW(B_1) , FOLLOW(B_2) , ... , FOLLOW(B_n)$两两相交均为空集，则文法$G$称为SLR(1)文法。

• SLR(1)文法，可用SLR(1)分析法;
• SLR(1)文法，是无二义性的；
• LR(0)文法，一定也是SLR(1)文法。

【例】

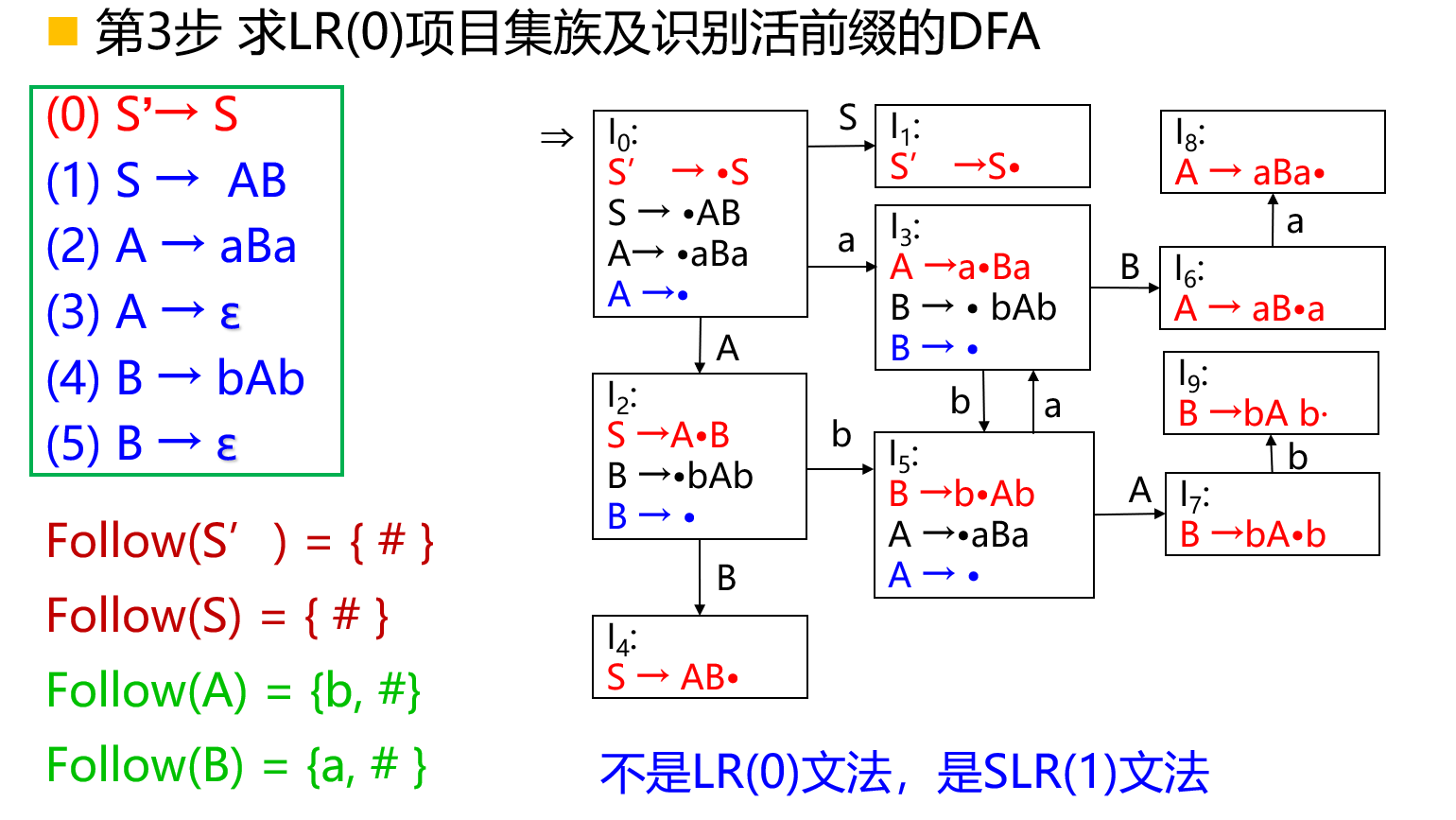
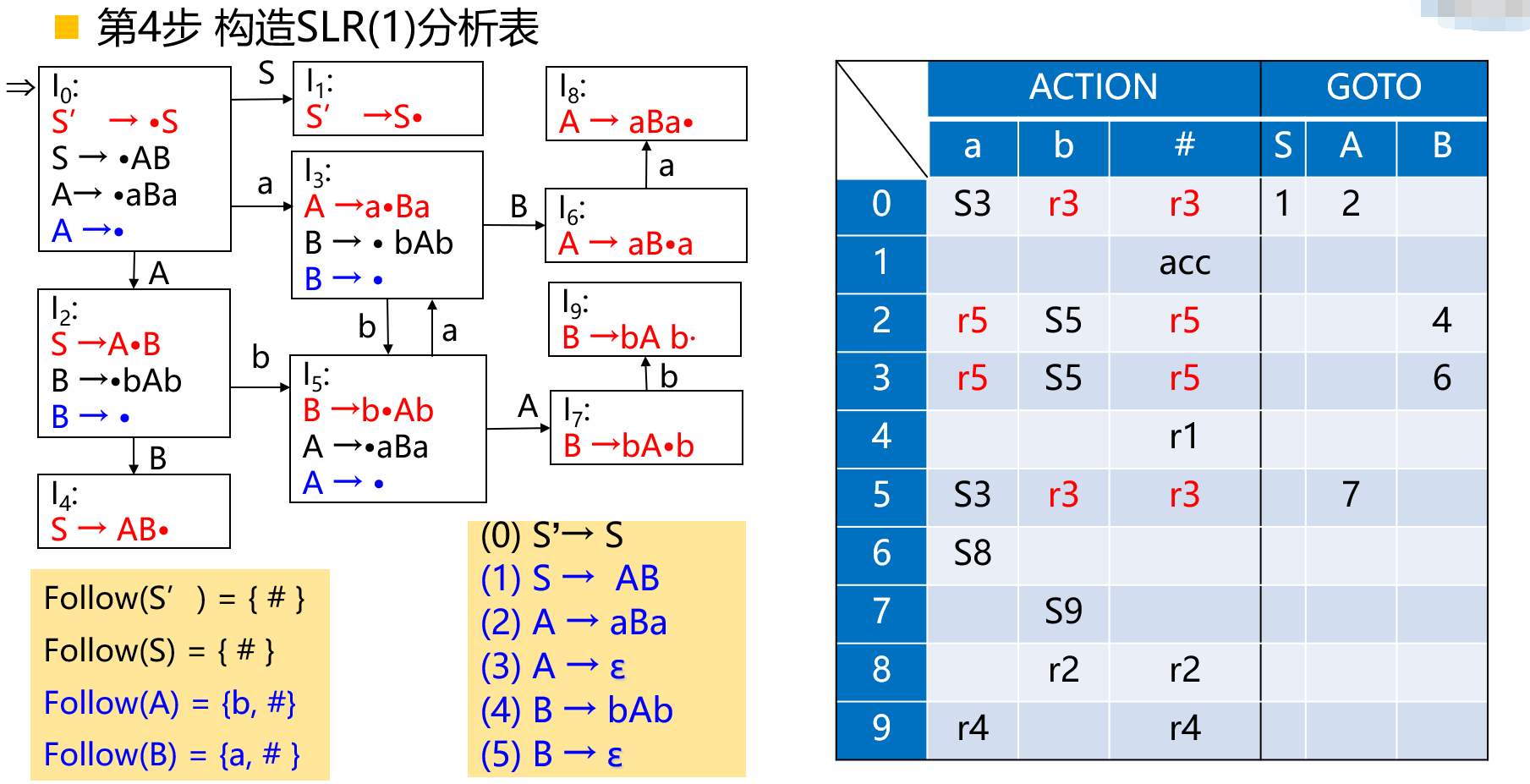
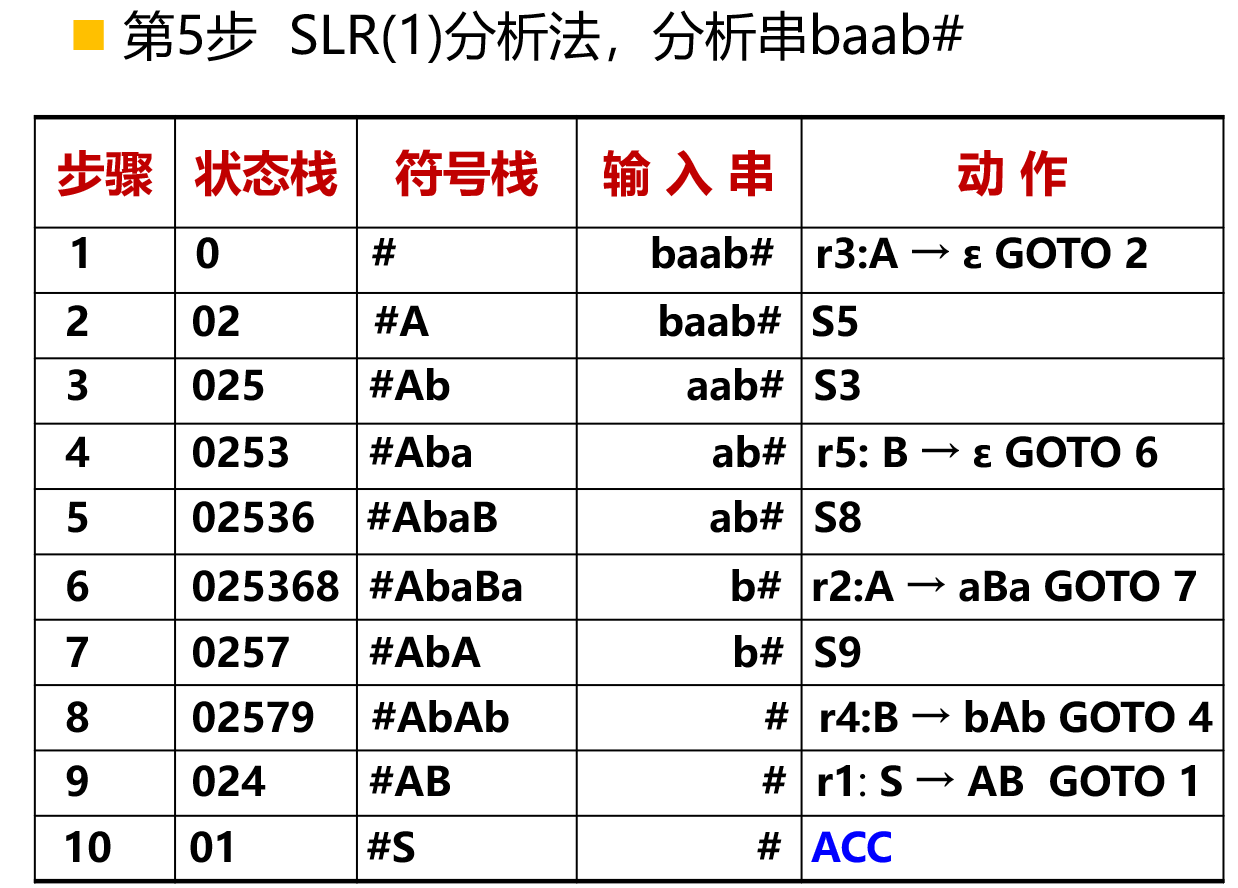
LR(1)分析

SLR(1)分析法存在的问题

• SLR只是简单地考察下一个输入符号$b$是否属于与规约项目$A \to \alpha$相关联的$FOLLOW(A)$，但$b \in FOLLOW(A)$只是归约$\alpha$的一个必要条件，而非充分条件；
• 对于产生式$A \to \alpha$的归约，在不同的使用位置，$A$会要求不同的后继符号；
• 在特定位置，$A$的后继符号集合是$FOLLOW(A)$的子集。

LR(1)分析法在构造项目时，将特定位置的后继符信息一并纳入考量范围。

LR(1)的基本思想

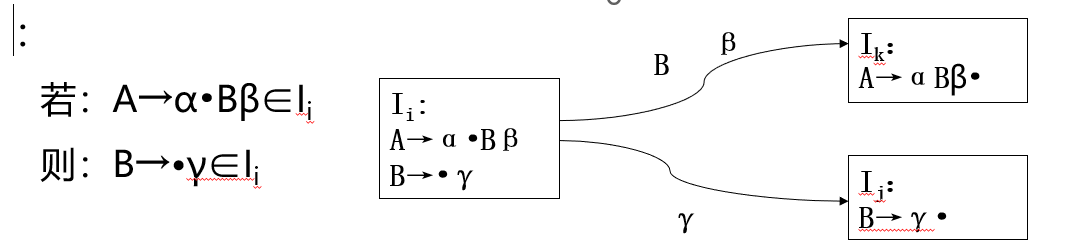
在状态$I_i$：下一个符号属于$FOLLOW(B)$而不属于$FIRST(\beta)$，即便归约到$B$，最终也会面临此路不通。

把$FIRST(\beta)$作为产生式作为$B \to \gamma$归约时向前查看的符号集合（向前搜索符号集，前瞻符号集），代替SLR(1)分析法中的$FOLLOW(B)$，并将向前搜索符号集也放在$LR(0)$项目的后面：

$[A \to \alpha \cdot \beta , a]$，$a$称为向前搜索符（展望符）-LR(1)项目

LR(1)项目

定义：附加搜索符（$\in V_T \cup \{\#\}$）的$LR(0)$项目称为$LR(1)$项目。记为$[LR(0)项目， 搜索符]$。$LR(1)$项目中$LR(0)$项目部分称为$LR(1)$项目的心。对于同心的$LR(1)$项目简记为$[LR(0)项目， 搜索符1|搜索符2|...| 搜索符m]$。后者称为搜索集。

形如$[A \to \alpha \cdot , a]$的项表示仅在下一个输入符号等于$a$时才可以按照$A \to \alpha$进行归约。

这样的$a$的集合总是$FOLLOW(A)$的子集，通常是真子集。

P68

定义：设$I$是文法$G$的$LR(1)$项目子集，则$MOVE1(I , X)$定义如下：

$$MOVE1(I , X) = \{[A \to \alpha X \cdot \beta , a] | [A \to \alpha \cdot X \beta , a] \in I\}$$

定义：设$I$是文法$G$的$LR(1)$项目子集，closure1(I)定义如下：

• $I \sub closure1(I)$；
• $\{[B \to \cdot \gamma] | [A \to \alpha \cdot B \beta , a] \in closure1(I) , b \in FIRST(\beta a)\} \sub closure1(I)$；
• 重复上一步，直到$closure1(I)$不再扩大为止。

LR(1)识别活前缀的DFA M构造

设文法$G = (V_N , V_T , P , S)$，等价改写文法$G'= (V_N \cup \{S'\} , V_T , P \cup \{S' \to S\} , S')$；其中$V_N \cap \{S'\} = \empty$，则识别活前缀$DFA\;M = (K , \sum , f , S , Z)$，其中：

• $K \subseteq p$（LR(1)项目集）；
• $\sum = V_N \cup V_T$；
• $f(I , X) = closure(MOVE1(I , X)) , I \in L , X \in \sum$；
• $S = closure1([S' \to \cdot S , \#])$；
• $Z = \{q , q \in K , q 含有归约项目\}$。

定义：文法$G$的$LR(1)$识别活前缀DFA M的状态集称为文法$G$的$LR(1)$项目规范族。

LR(1)分析表的构造

设文法$G$的$LR(1)$项目集规范族$C = \{I_0 , I_1 , ... , I_n\}$；

对$C$中每个$I_i$构造得到状态$i$，状态$i$的语法分析动作按照下面的方法决定：

• 如果$[A \to \alpha \cdot a \beta , b] \in I_i$并且$f(I_i , a) = I_j$，则$ACTION[i , a] = S_j$；
• 如果$[A \to \alpha \cdot B \beta , b] \in I_i$并且$f(I_i , B) = I_j$，则$ACTION[i , B] = S_j$；
• 如果$[A \to \alpha \cdot , a] \in I_i$并且$A \neq S'$，则$ACTION[i , a] = r_j$；（$j$是产生式 的编号）
• 如果$[S' \to S \cdot , \#] \in I_i$，则$ACTION[i , \#] = acc$；
• 所有没有定义的条目都设置为$e_t$，$t$是错误编号。

定义：设文法$G$的$LR(1)$项目集规范族$C$中任意含有$m$个移进项目和$n$个归约项目的冲突项目集$I_k$的一般形式为：$I_k = \{[A_1 \to \alpha_1 \cdot a_1 \beta_1, S'_1], ... ,[A_m \to \alpha_m \cdot a_m \beta_m , S'_m] , [B_1 \to \gamma_1 \cdot , S_1],... , [B_n \to \gamma_n \cdot , S_n], ...\}$。

其中$A_i , B_j \in V_N , a_i \in V_T , \alpha_i , \beta_j , \gamma_q \in (V_N \cup V_T)^* , ...$表示剩下的待约项目，$S'_i , S_j$为搜索集。

如果移进符号集$\{a_1 , a_2 , ... , \alpha_m\}$和搜索集$S_1 , ... , S_n$两两相交均为空集，则文法$G$称为$LR(1)$文法。

• 如果文法$G$是$LR(1)$文法，则$G$可采用$LR(1)$分析法；
• 如果文法$G$是$LR(1)$文法，则$G$是无二义性的；
• 如果文法$G$是$SLR(1)$文法，则$G$一定是$LR(1)$。

【例】

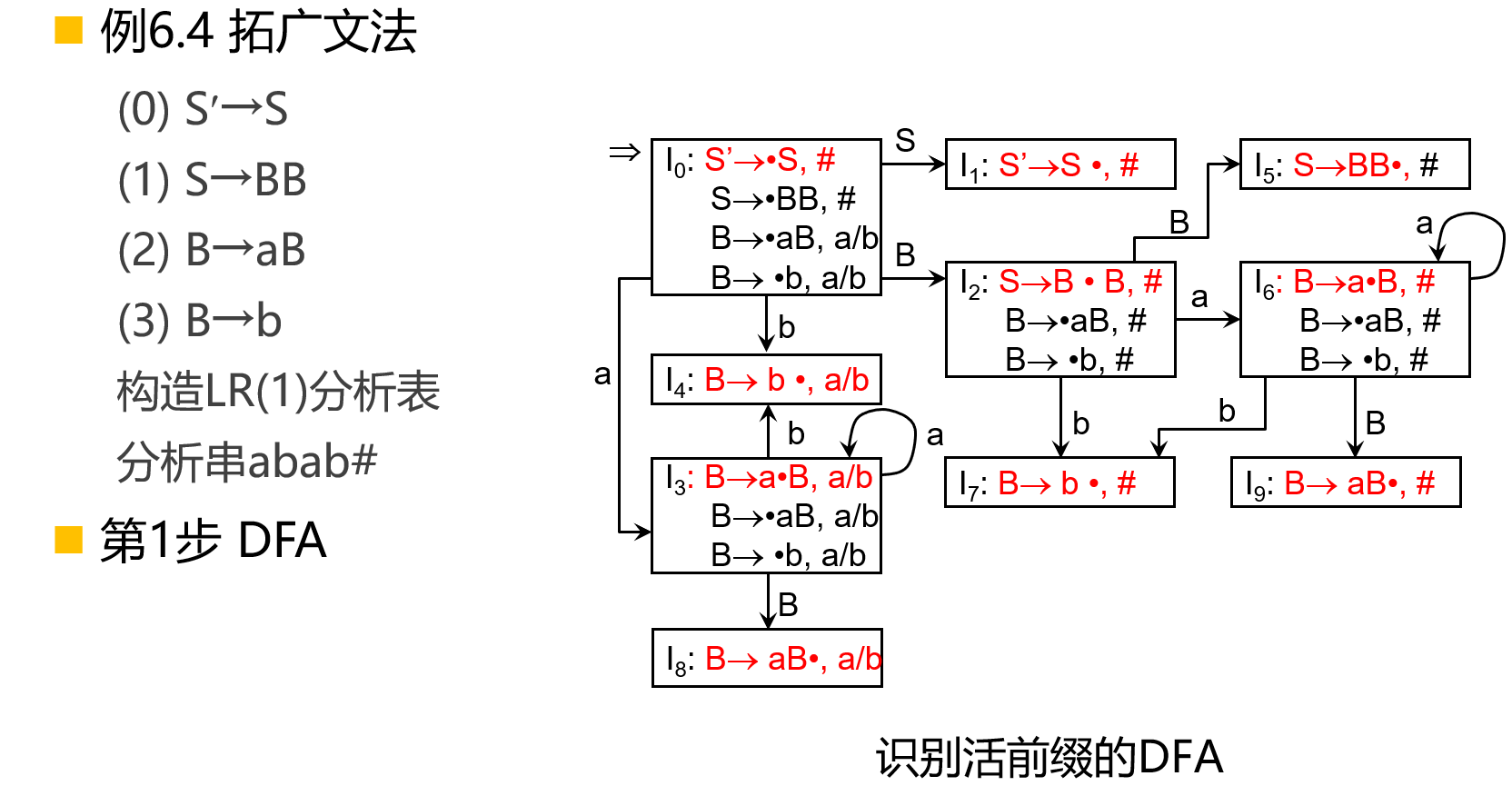
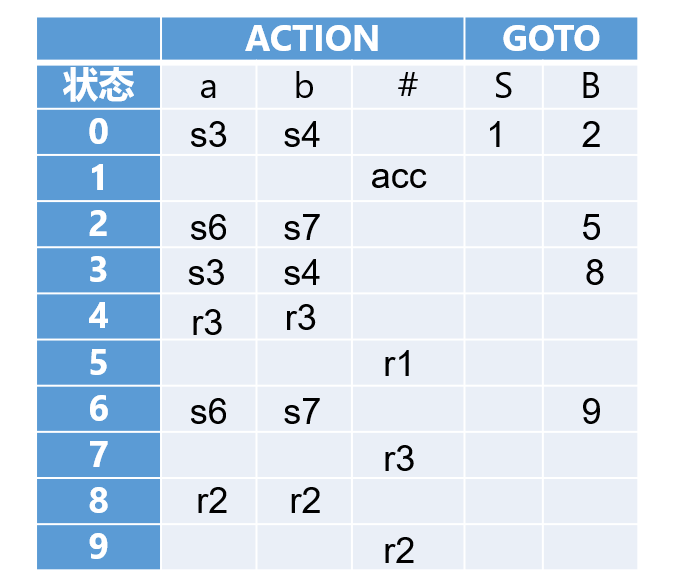
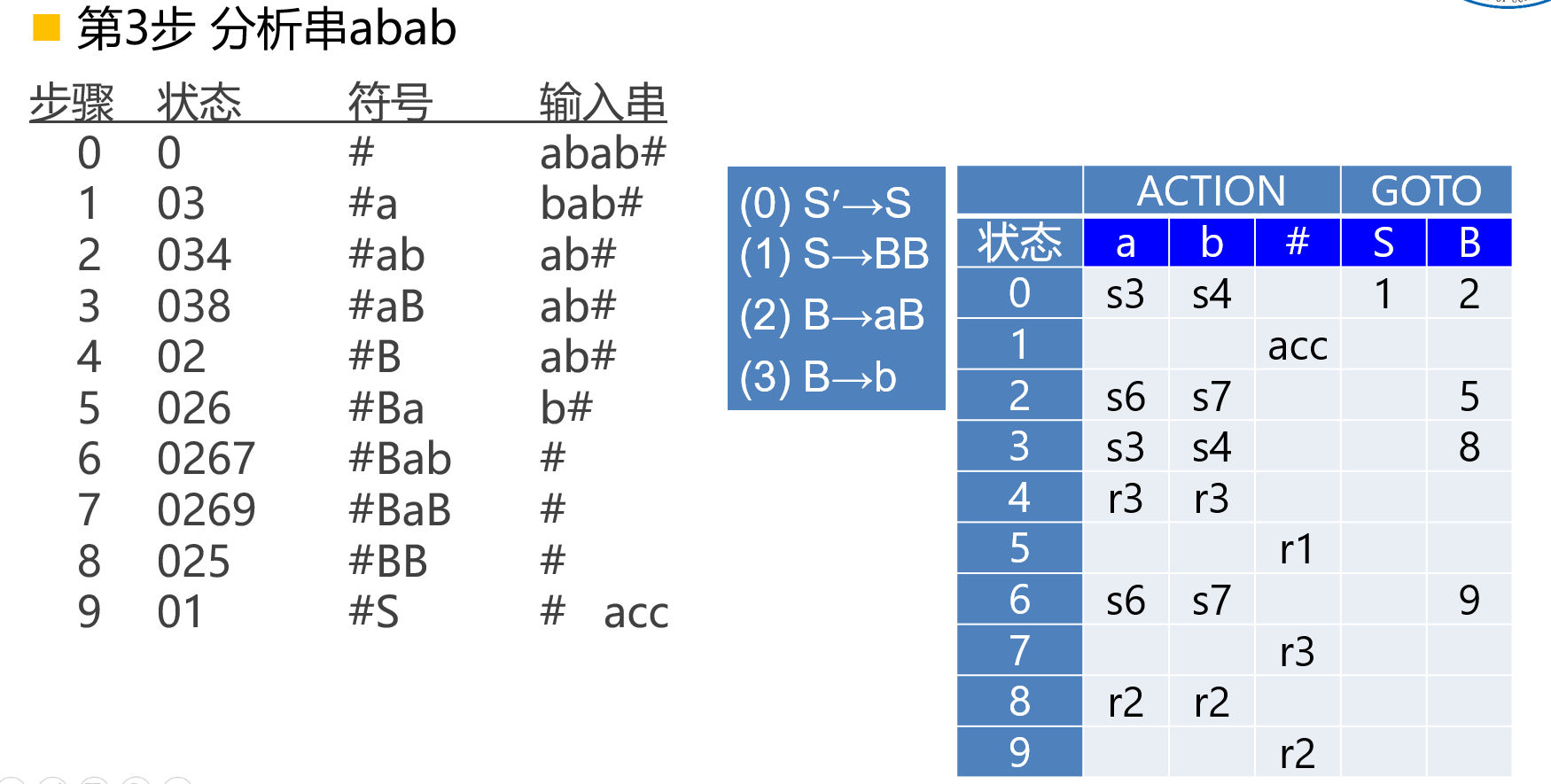
LALR(1)分析

定义：如果采用同心项目集合并方法，进行合并后的文法$G$的$LR(1)$项目集规范族，没有$LR(1)$项目冲突，则称文法$G$为$LALR(1)$文法。

关于$LALR(1)$文法，可以得出下列几个结论：

• 如果文法$G$是$LALR(1)$文法，则$G$可采用$LALR(1)$分析法；
• 如果文法$G$是$LALR(1)$文法，则$G$是无二义性的；
• 如果文法$G$是$LALR(1)$文法，则$G$一定是$LR(1)$文法。

【例】

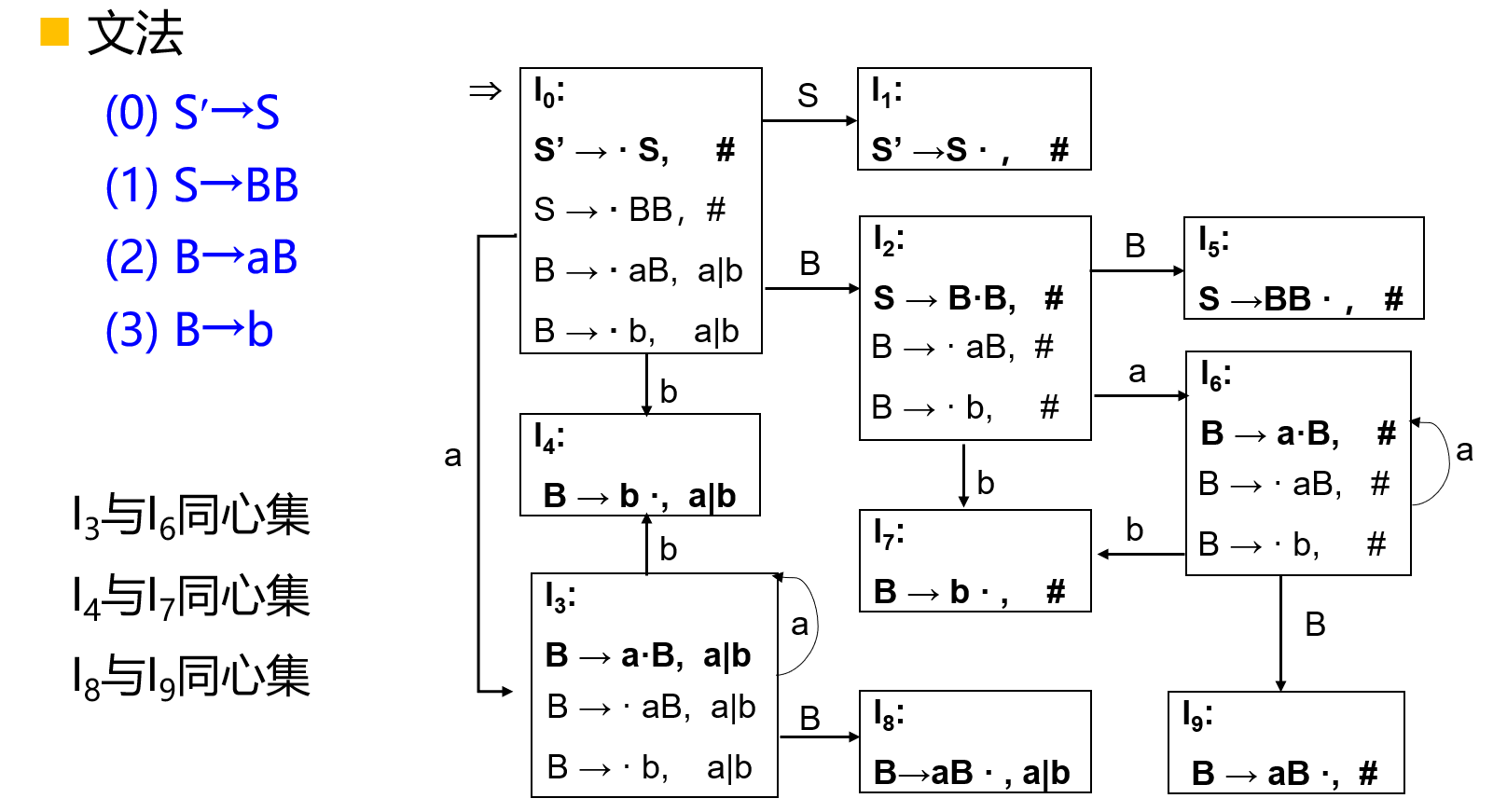
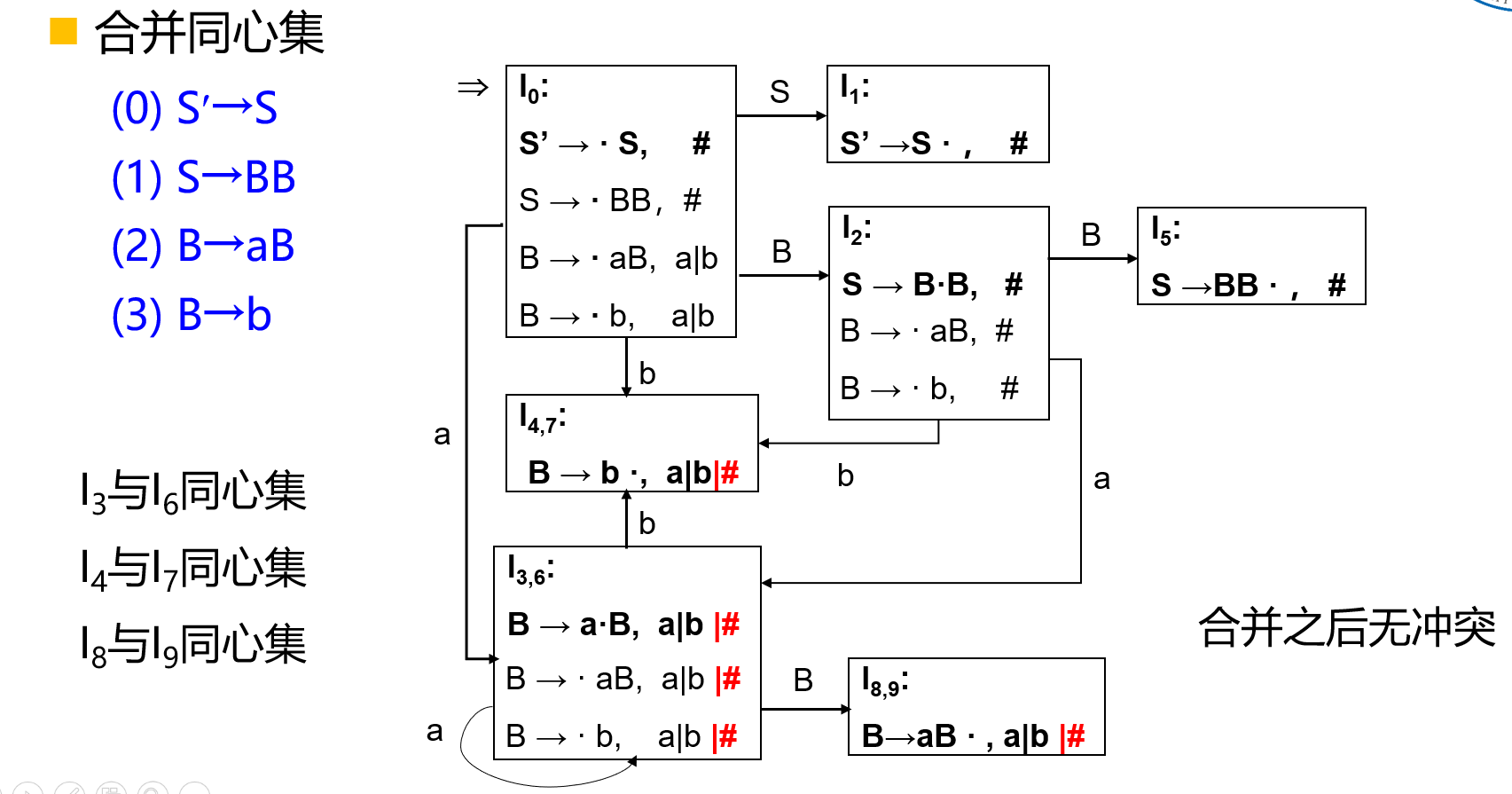
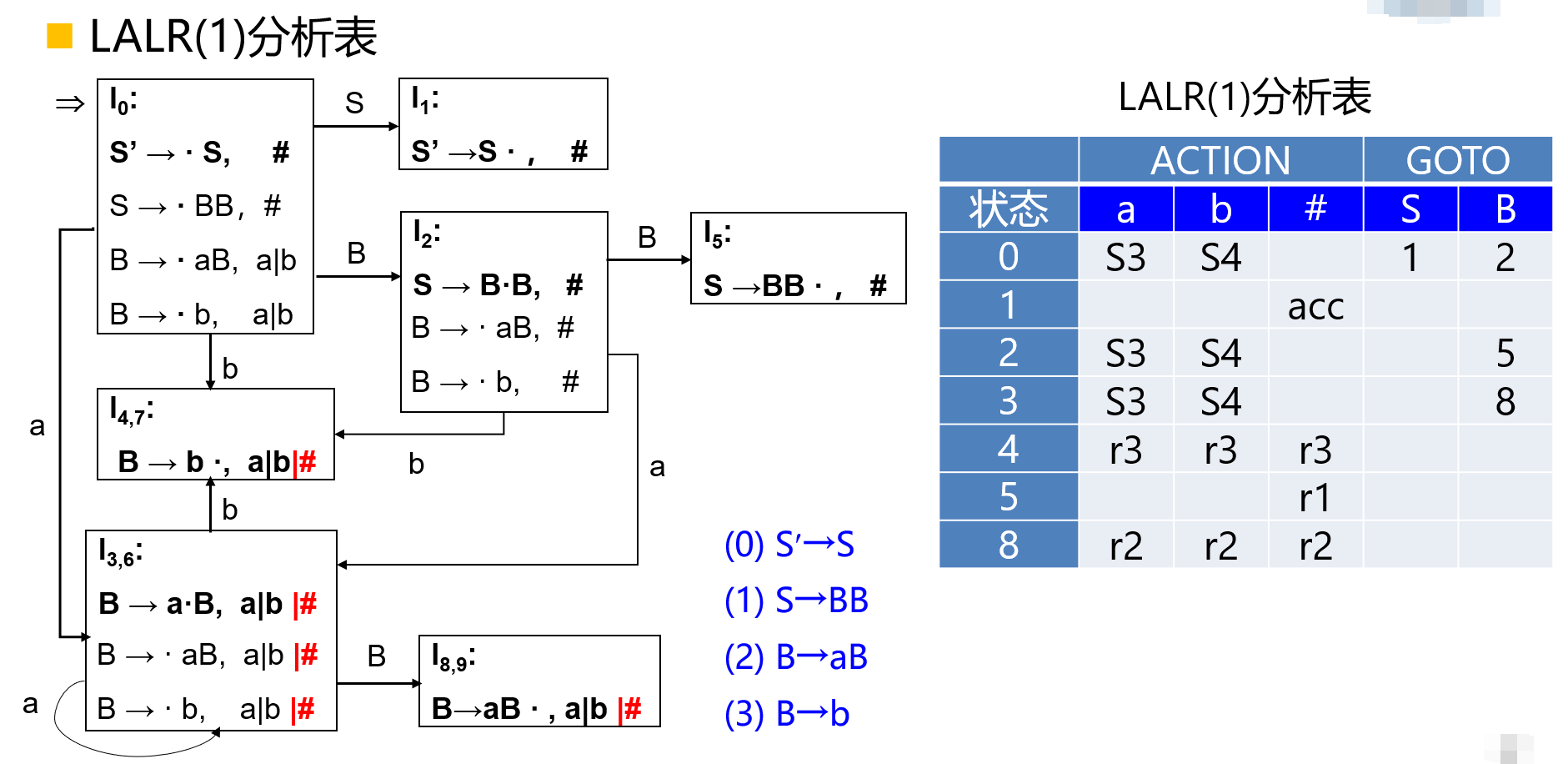
LALR(1)的特点

• 形式上与$LR(1)$相同；
• 大小上与$LR(0) / SLR$相当；
• 分析能力介于$SLR$和$LR(1)$二者之间；
• 合并后的向前搜索符集合仍为$FOLLOW$集的子集。