第五章自底向上优先分析

自底向上优先分析

\(Notes\)：由于某符号打不出来，所以用\(\doteq\)代替等号中间一个点。

优先分析概述

移进—归约法：根据文法寻找句型的句柄

优先分析法：利用句型相邻两个符号之间的优先级关系确定句柄

\(if\;(x \lessdot \doteq a_i) \;shift(a_i);else\;if (x \gtrdot a_i) reduce(A \to ...x);else\;error();\)

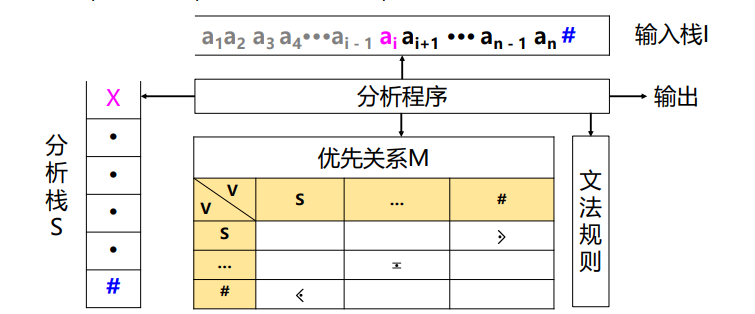
简单优先分析法

定义：设文法\(G = (V_N , V_T , P , S)\)，则\((V_N \cup V_T)\)上的\(3\)种优先关系定义如下（二元关系）：

• \(X \doteq Y , iff\;A \to ...XY... \in P\)；
• \(X \lessdot Y,iff\;A \to ...XB...\in P , B \stackrel{+}{\Rightarrow} Y...\)；
• \(X \gtrdot Y , iff\;A \to ...BD... \in P , B \stackrel{+}{\Rightarrow} ...X ,D \stackrel{*}{\Rightarrow} Y...\)；

其中\(X , Y , D \in (V_N \cup V_T) , A, B \in V_N , ... \in (V_N \cup V_T)^*\)。

特别地，句子括号\(\#\)的优先级低于其右邻符号，其左邻符号优先级高于\(\#\)；优先级关系在句型中相邻的符号，反映了归约时的优先关系：

• \(X \doteq Y\)：表示在句型中相邻出现的\(XY\)，同时被归约；
• \(X \lessdot Y\)：表示在句型中相邻出现的\(XY\)，X后于Y被归约；
• \(X \gtrdot Y\)：表示在句型中相邻出现的\(XY\)，X先于Y被归约。

定义：文法\(G\)的符号集\(V\)中，任意两个符号之间至多存在\(\doteq , \lessdot , \gtrdot\)三种简单优先关系之一，且没有相同右部的规则，则文法\(G\)称为简单优先文法。

关于简单优先文法，可以证明下列几个结论：

• 设文法\(G\)为简单优先文法，句型\(\#a_1a_2...a_{i - 1}a_{i}a_{i + 1}...a_{j - 1}a_{j}a_{j + 1}...a_n\#\)，存在下列关系：

  \(a_{i - 1} \lessdot a_i \doteq a_{i + 1} \doteq ...\doteq a_{j} \gtrdot a_{j + 1}\)，则子串\(a_ia_{i+ 1}...a_{j - 1}a_j\)是句型的直接短语。

• 设文法\(G\)为简单优先文法，如果输入串或归约后的符号串中相邻的两个符号之间不存在任何一种简单优先关系，则输入串不是文法的句子。

• 如果文法\(G\)是简单优先文法，则文法\(G\)是无二义性的文法。

简单优先分析法的思想

1. 初始化：\(\#\)入分析栈\(S\)，\(w\#\)入输入栈\(I\)，\(\#\)在栈底；

2. \(X = top(S);a = top(I)\)；

3. \(if\;(x \lessdot \doteq a_i) \;shift(a_i);else\;if (x \gtrdot a_i) reduce(A \to ...x);else\;error();\)

   在\(S\)栈顶寻找以下关系序列，以确定句柄的首部：

   \(a_{i - 1} \lessdot a_i \doteq ...\doteq X \gtrdot a\)，确定句柄为\(a_i...X\)，再用\(A \to a_i...X\)归约

4. 重复2 3，直到归约出文法开始符\(S\)（\(\#S\)）。

简单优先文法中任何两个符号之间优先关系保存在优先关系矩阵中。\(M[X , Y]\)存放\(3\)个优先关系符号\(\doteq , \lessdot , \gtrdot\)和空白之一。

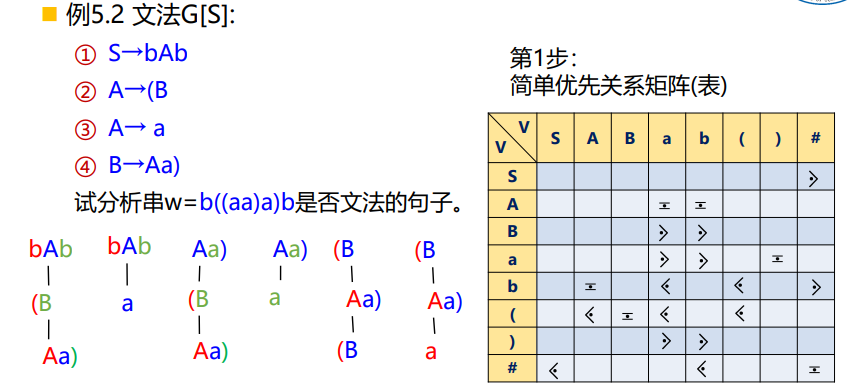
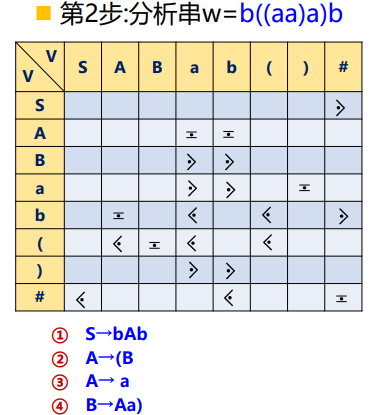
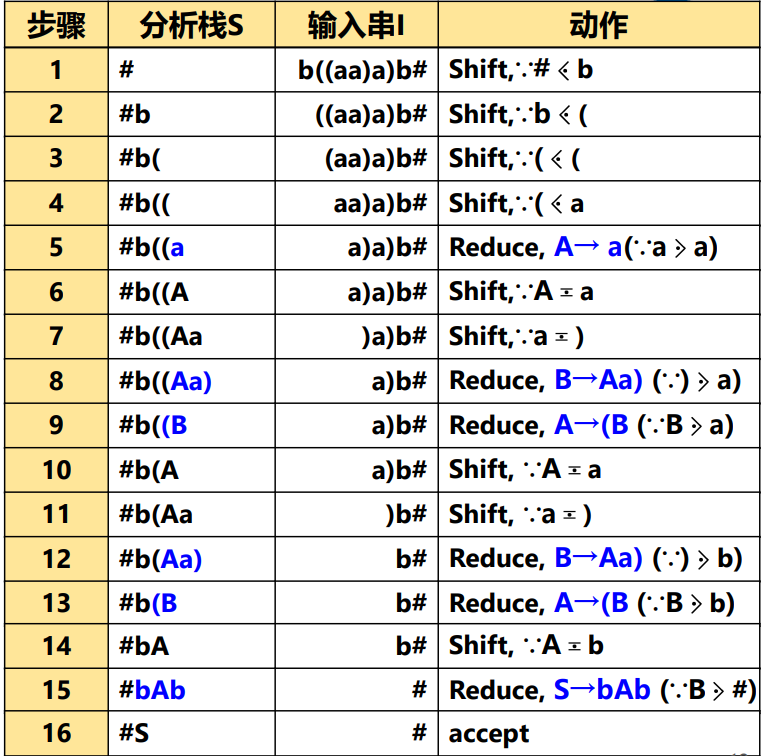
【例】

【例】

算符优先分析法

• 与简单优先分析法不同，算符优先分析法仅仅利用相邻的两个终结符之间优先关系寻找归约子串。这个归约子串不是句柄，但它是一种特殊的直接短语，被称为最左素短语。
• 这种分析法源于对表达式处理。表达式是计算机语言中最重要的、最核心的组成部分，其语法特点是表达式运算符合和运算对象组成。表达式组成是否符合语法，通常是以运算符的计算优先顺序和运算符需要运算对象个数进行判别的。

定义：设文法\(G = (V_N , V_T , P , S)\)，如果\(G\)中没有形如\(A \to ... BC ...\)的规则，其中\(A , B , C \in V_N\)，则称文法\(G\)为算符文法（Operator Grammer），简称OG文法。

例如：表达式文法（有二义性的，无二义性但有左递归）均是OG文法。OG文法其实质是对规则进行了限制，也就是规则右部不得出现两个非终结符直接相邻。它是对表达式进行形式化和推广，终结符均为算符，非终结符视为运算结果。

• 性质1：在OG文法中任何句型都不包含两个相邻的非终结符。
• 性质2：如果Ab或bA出现在OG文法的句型\(\gamma\)中，其中\(A \in V_N , b \in V_T\)，则句型\(\gamma\)中任何包含此b的短语必含有A。

定义：设算符文法\(G = (V_N , V_T , P , S)\)，\(V_T\)上的\(3\)种算符优先关系定义如下：

• \(a \doteq b , iff\;A \to ...ab... \in P\)，或\(A \to ...aBb... \in P\)；
• \(a \lessdot b , iff\;A \to ...aB... \in P , B \stackrel{+}{\Rightarrow} b...\)或\(B \stackrel{+}{\Rightarrow}Cb...\)；
• \(a \gtrdot b , iff\;A \to ...Bb... \in P , B \stackrel{*}{\Rightarrow} ...a , B \stackrel{+}{\Rightarrow}...aC\)；

其中\(a , b \in V_T , A , B , C \in V_N , ... \in (V_N \cup V_T)^*\)。

算符优先关系在句型中相邻的符号，反映了归约时的优先关系。即：

• \(a \doteq b\)：在句型中相邻出现的\(ab\)或\(aBb\)，同时被归约；
• \(a \lessdot b\)：在句型中相邻出现的\(ab\)或\(aBb\)，\(a\)晚于\(b\)被归约；
• \(a \gtrdot b\)：在句型中相邻出现的\(ab\)或\(aBb\)，\(a\)先于\(b\)被归约。

定义：设不含空规则的文法\(G\)为\(OG\)文法，如果任意两个终结符之间至多存在\(\doteq , \lessdot , \gtrdot\)三种运算符优先关系之一，则称文法\(G\)为算符优先文法（Operator Precedence Grammar），简称OPG文法。

【例】

算符优先文法是无二义性文法

定义：设文法\(G[S]\)，其句型的素短语是满足下列两个条件的短语：

• 至少含有一个终结符。
• 除自身外不包含其它素短语。

特别地，最左边的素短语称为最左素短语。

【例】

最左素短语定理：一个算符优先文法\(G\)的任何句型\(\#N_1a_1N_2a_2...N_{i - 1}a_{i - 1}N_ia_iN_{i + 1}a_{i + 1}...N_{j - 1}a_{j - 1}N_ja_jN_{j + 1}a_{j + 1}...N_na_n\#\)，其中\(a_i\)都是终结符，\(N_i\)是可有可无的非终结符。该句型的最左素短语是满足如下条件的最左子串\(N_ia_i...N_ja_jN_{j + 1}\)：

• \(a_{i - 1} \lessdot a_i \doteq ...\doteq a_j \gtrdot a_{j + 1}\)

设文法\(G\)为算符优先文法，如果输入串货归约后的符号串中，相邻的两个符号之间，不存在任何一种算符优先关系，则输入串不是文法的句子。

如果文法\(G\)是算符优先文法，则文法\(G\)是无二义性的文法。

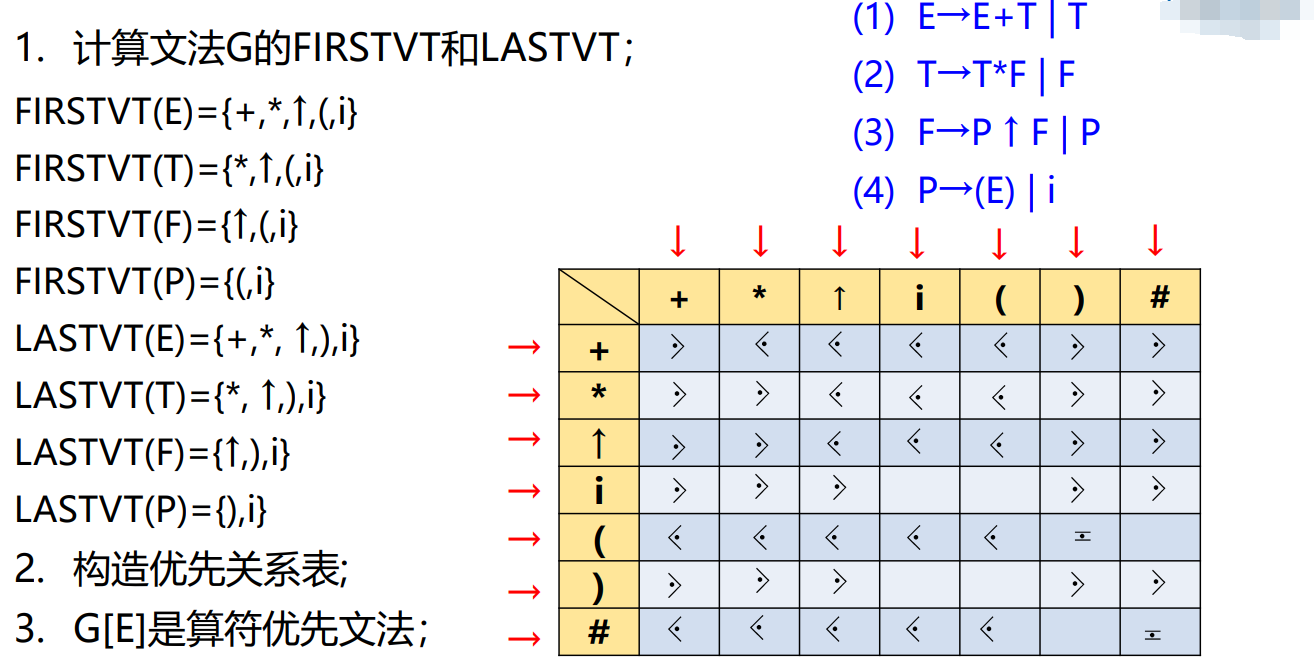
定义：设文法\(G = (V_N , V_T , P , S)\)，则FIRSTVT(B)和LASTVT(B)定义如下：

• \(FIRSTVT(B) = \{a | B \stackrel{+}{\Rightarrow}a...\;or\;B \stackrel{+}{\Rightarrow}Ca... , a \in V_T , C \in V_N\}\)；
• \(LASTVT(B) = \{a | B \stackrel{+}{\Rightarrow}...a\;or\;B \stackrel{+}{\Rightarrow}...Ca , a \in V_T , C \in V_N\}\)；

FIRSTVT(B)集计算方法：

1. \(FIRSTVT(B) = \empty\)；
2. 扫描文法规则，对形如\(B \to a...\)或\(B \to Ca...\)规则，\(a \in V_T , C \in V_N\)，择\(FIRSTVT(B) \cup = \{a\}\)；
3. 扫描文法规则，对形如\(B \to C...\)规则，\(C \in V_N\)，则\(FIRST(B) \cup = FIRSTVT(C)\)；
4. 重复\(3\)，直到\(FIRSTVT\)集不再扩大为止。

LASTVT(B)集计算方法：

1. \(LASTVT(B) = \empty\)；
2. 扫描文法规则，对形如\(B \to ...a\)或\(B \to ...aC\)规则，\(LASTVT(B) \cup = \{a\}\)；
3. 扫描文法规则，对形如\(B \to ...C\)规则，\(C \in V_N\)，则\(LASTVT(B) \cup= LASTVT(C)\)；
4. 重复\(3\)直到\(LASTVT\)集不再扩大为止。

基于FIRSTVT(B)和LASTVT(B)的运算符优先关系计算：

• 如果\(A \to ...ab... \in P\)或\(A \to ...aBb... \in P , a , b \in V_T , B \in V_N\)，则\(a \doteq b\)；
• 如果\(A \to ...aB...\in P , b \in FIRSTVT(B),a \in V_T , B \in V_N\)，则\(a \lessdot b\)；
• 如果\(A \to ...Bb... \in P , a \in LASTVT(B) , b \in V_T , B \in V_N\)，则\(a \gtrdot b\)。

【例】

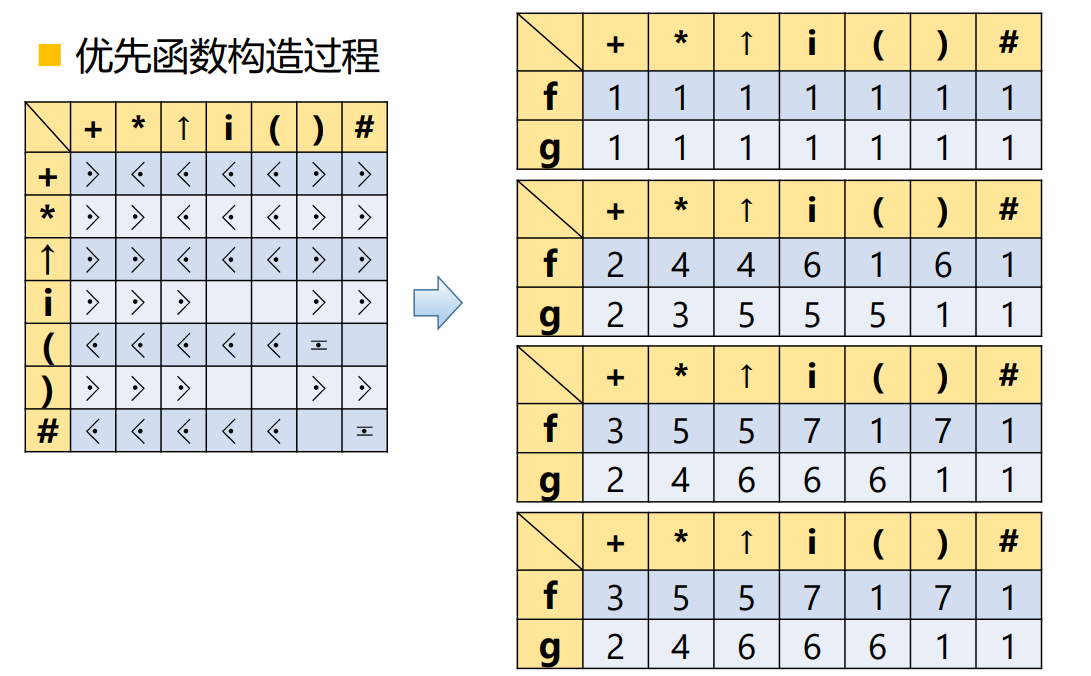
定义：设文法\(G = (V_N , V_T , P , S)\)，算符优先关系为\(\doteq , \lessdot , \gtrdot\)，定义在\(V_T \to N^+\)上的函数\(f\)和\(g\)满足下列条件，则文法\(G\)的\(f\)和\(g\)称为算符优先函数：

• \(a \doteq b\;iff\;f(a) = g(b)\)；
• \(a \lessdot b\;iff\;f(a) < g(b)\)；
• \(a \gtrdot b\;iff\;f(a) > g(b)\)。

优先函数与算符优先矩阵：\(2(|V_T| + 1)\) vs \((|V_T| + 1)^2\)。

算符优先函数的构造：

• 对\(a \in V_T\)，置\(f(a) = g(a) = 1\)；
• 对每个关系偶对\(<a , b>\)，按下列情况分别计算：
  • 如果\(a \doteq b , f(a) \neq g(b)\)，则\(f(a) , g(b) = max(f(a) , g(b))\)；
  • 如果\(a \lessdot b , f(a) \geq g(b)\)，则\(g(b) = f(a) + 1\)；
  • 如果\(a \gtrdot b, f(a) \leq g(b)\)，则\(f(a) = g(b) + 1\)；
• 重复第二个步骤，直到\(f\)和\(g\)函数不再变化（或称过程收敛），或者\(f\)和\(g\)函数有值大于\(2|V_T|\)为止。后一种情况判定\(f\)和\(g\)函数不存在。

【例】

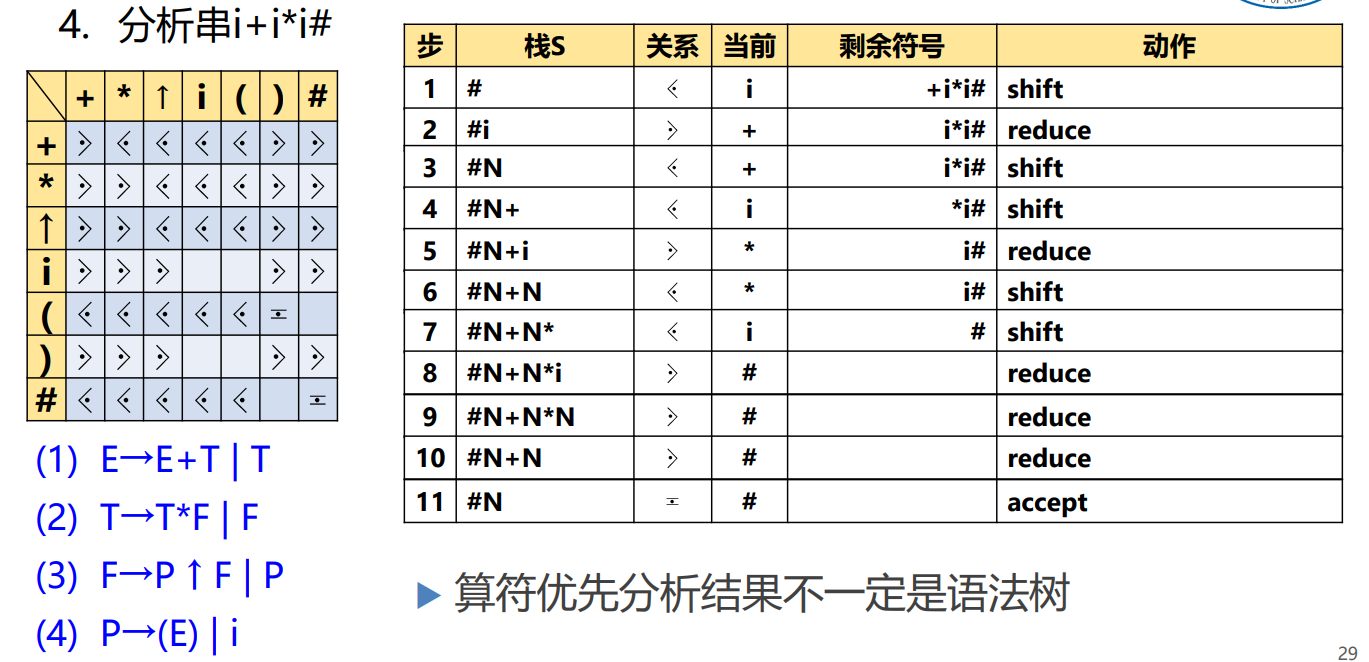
算符优先分析法的优缺点：

• 优点：简单、快速
• 缺点：可能错误接受非法句子

算符优先分析法的主要应用场景：

• 用于分析各类表达式