第三章词法分析
作者:@cherish.
课程学习内容为作者从学校的PPT处摘抄,仅供自己学习参考,若需转载请注明出处:https://www.cnblogs.com/cherish-/p/16370927.html
词法分析
单词的形式化描述工具
- 基于生成观点、计算机观点和识别观点,分别形成了正规文法、正规式和有穷自动机种用于描述词法的工具。
正规文法
设文法,如果任意,且只能是或或,则称文法属于右线性型文法。
正规式及其表达的语言
也称为正则表达式,其表达的语言称为正规集。
- 对给定的字母表
- 和都是正规式,其正规集分别是和
- ,是上的正规式,其正规则集为
- 如果和都是上的正规式,则(算符优先级由高到低位:*, ,|)
- 是正规式,它表示的正规集为
- 是正规式,它表示的正规集为
- 是正规式,它表示的正规集为
- 是正规式,它表示的正规集为
- 有限次使用上述步骤而定义的表达式仍是正规表达式,它们表示的符号串的集合是正规集。
【例】:令,则上正规式和对应的正规集如下:
| 正规式 |
正规集 |
|---|---|
-
所有词法结构一般都可以用正规式描述
-
若两个正规式所表示的正规集相同,则称这两个正规式等价,如。
-
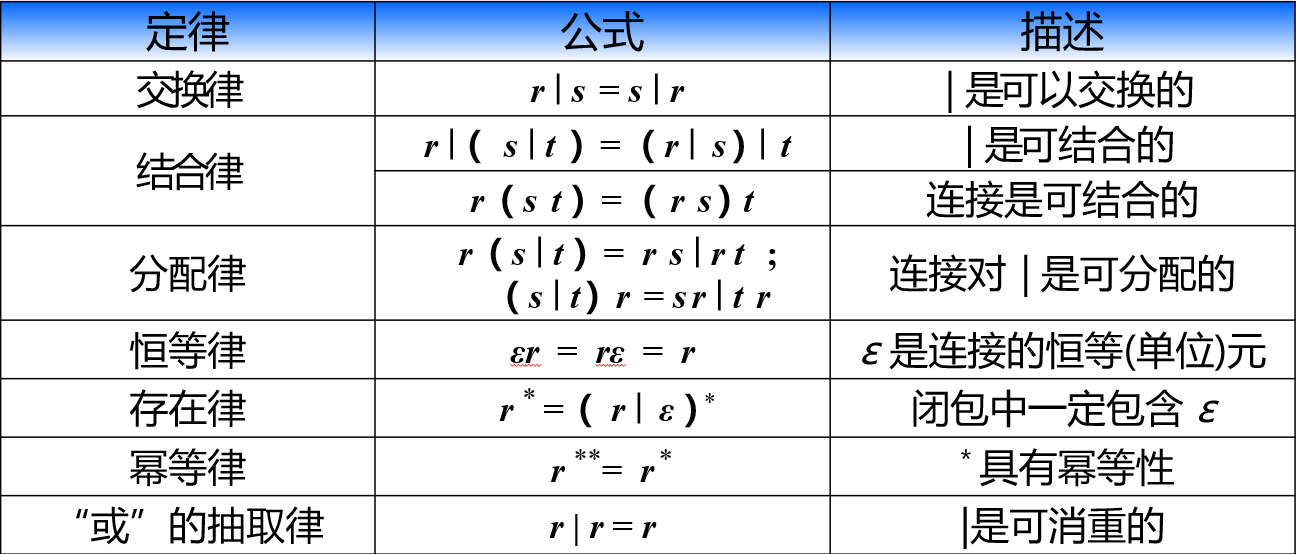
正规式的代数定律:设为正规式,则有:
正规式和正规文法之间转换
- 如果正规式和正规文法,有则称正规式和文法是等价的。
正规式文法转换方法
-
设上正规式,则等价文法。其中;从形如产生式开始,按下表规则进行转换,直到全部形如产生式,符合正规文法指规则形式为止,可得到。
-

-

正规文法转换成正规式
-
基本上是正规式到正规文法的逆过程,按下列规则将文法处理成只剩下一个开始符号定义的正规式。
-

-
注意此处规则与前面的区别
-

有穷自动机
本质上和状态转换图相同,但有穷自动机只回答Yes/No。
分为两类:
- 不确定的有穷自动机
NFA:输入符号包括,一个符号可以标记在离开同一状态的多条边上 - 确定的有穷自动机
DFA:输入符号不含,每个状态以及每个符号最多只有一条边
两种自动机都识别正则语言,对于每个可以用正则表达式描述的语言,均可用某个NFA或DFA来识别;反之亦然。
确定的有穷自动机DFA
DFA形式化定义
-
确定有穷自动机
DFAM是一个五元组,其中:- :有穷状态集。
- :输入字母表(有穷),输入符号集。
- :状态转移函数,为的单值部分映射,表示:当现行状态为;输入字符为时,将状态转移到下一状态,称为的一个后继状态。
- :初始状态。
- :终态集,也称可接受状态或结束状态。
DFA的扩展状态转移函数
-
映射。设,即()
-
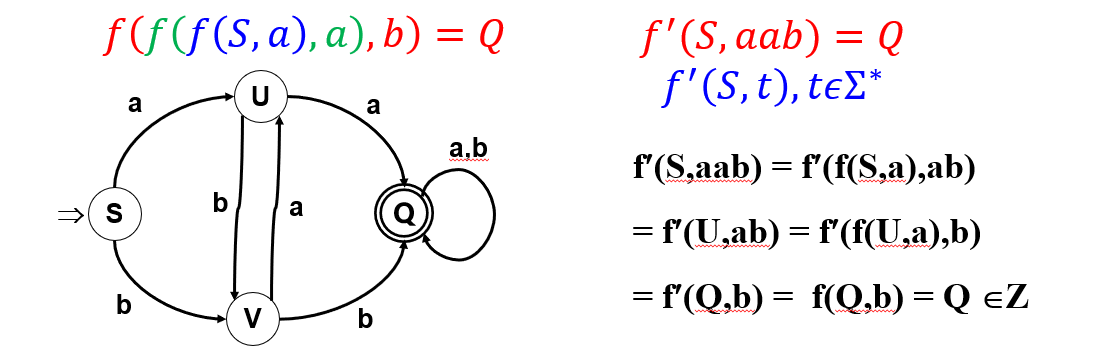
DFA识别的语言
-
设
DFA M= ,如果,则称符号串是DFA M所接受(或识别)的。DFA M所接受的符号串的集合记为: -
上的一个符号串集是正规的,当且仅当存在一个上的
DFA,使得。
非确定有穷自动机NFA
一个非确定有穷自动机NFA M是一个五元组,其中:
- :有穷状态集。
- :输入字母表(有穷)。
- :状态转移函数,为的部分映射,表示的幂集。
- :初始状态
- :终态集
【例】
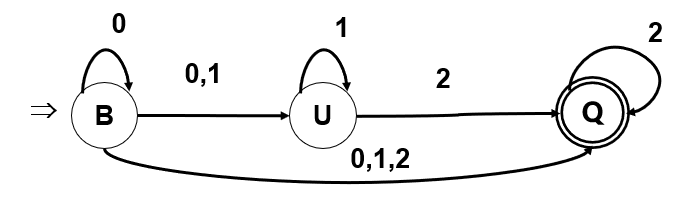

NFA扩展状态转移函数:
映射。
设,即:
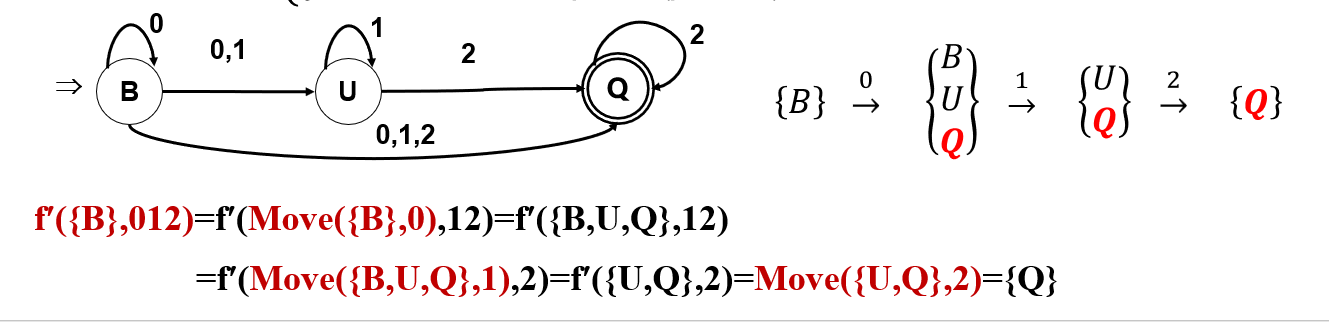
NFA识别的语言
设NFA M = ,如果,则称符号串是NFA M所接受(或识别)的。NFA M所接受的符号串的集合亦记为,即:
自动机的等价
对于任何两个有穷自动机和,如果,则称与等价。
对于每个NFA M存在一个DFA M,使得,反之亦然。
DFA与NFA描述能力相同
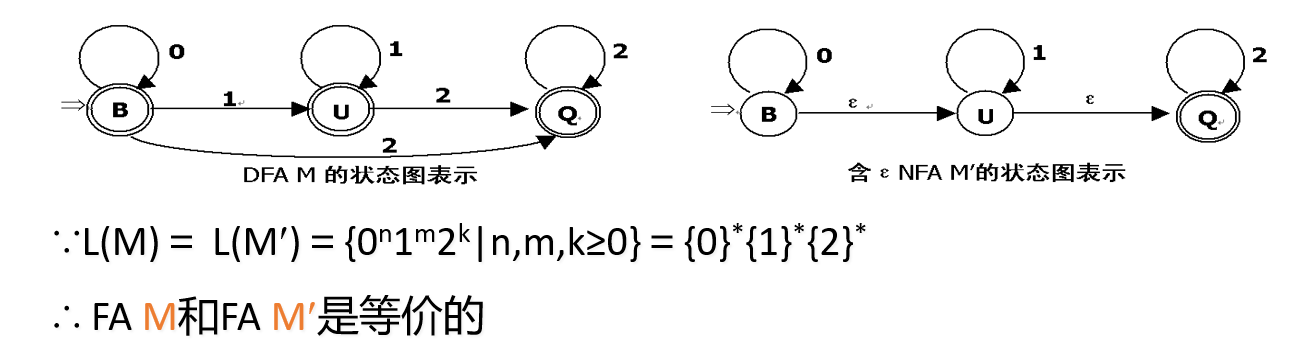
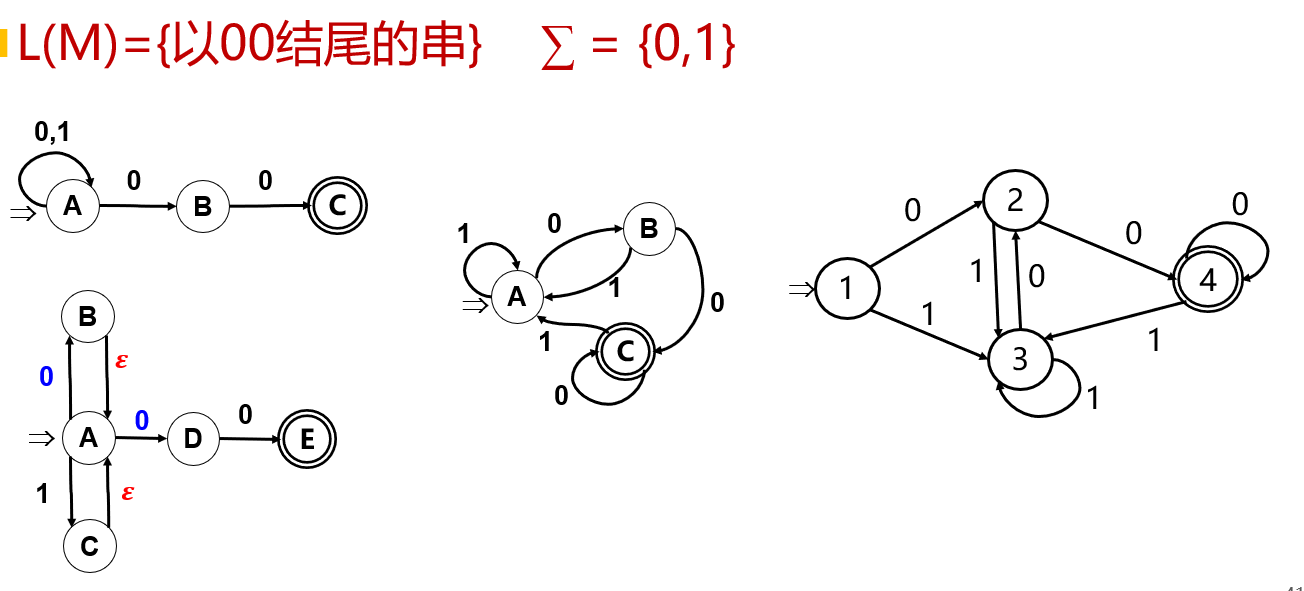
状态集I的转换运算
设NFA M = ,则定义如下:
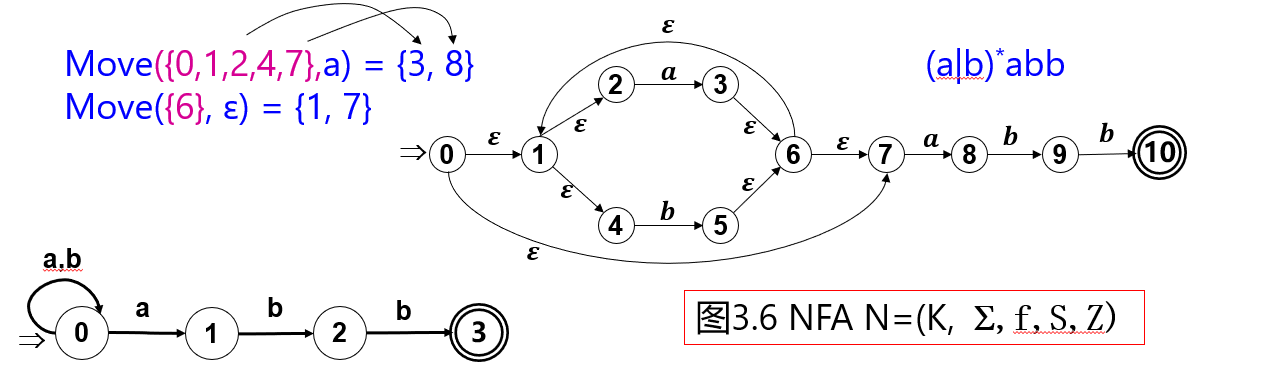
状态集的
设NFA M = ,则定义如下:
- 重复上一步,直到不再扩大为止。
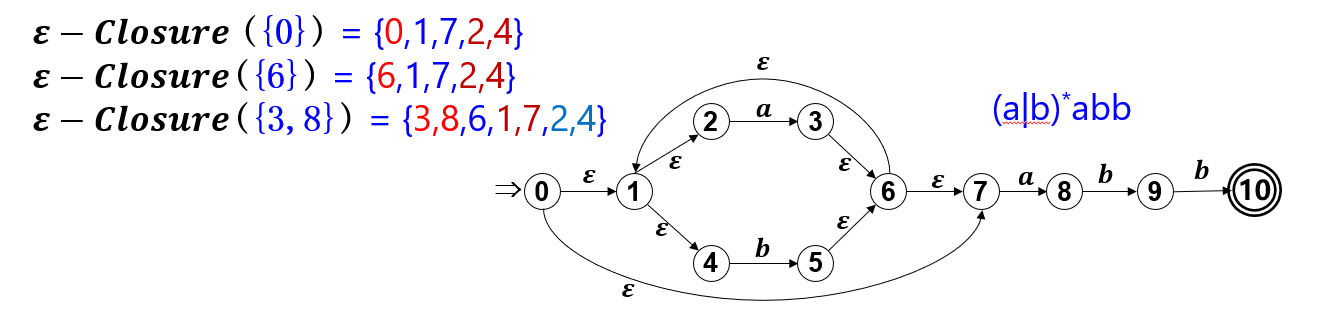
NFA到DFA的转换算法(子集构造法)
-
输入:
NFA N= -
输出:等价的
DFA D= ;。 -
方法:一开始是中的唯一状态,且它未加标记:
while(在D中有一个未标记状态T){ 给T加上标记; for(每个输入符号a){ U = ε-closure(move(T , a)); if(U不在D中) 将U加入D中,且不加标记; Dtran[T , a] = U; } } -
【例】
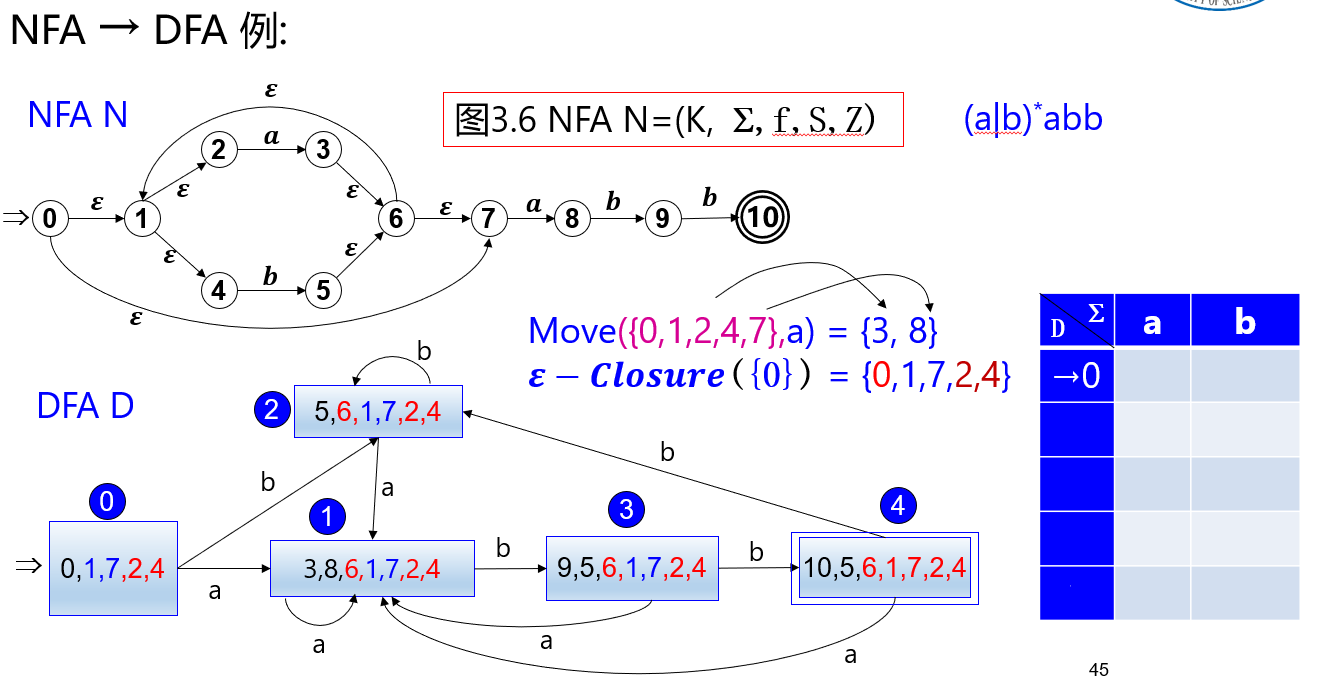
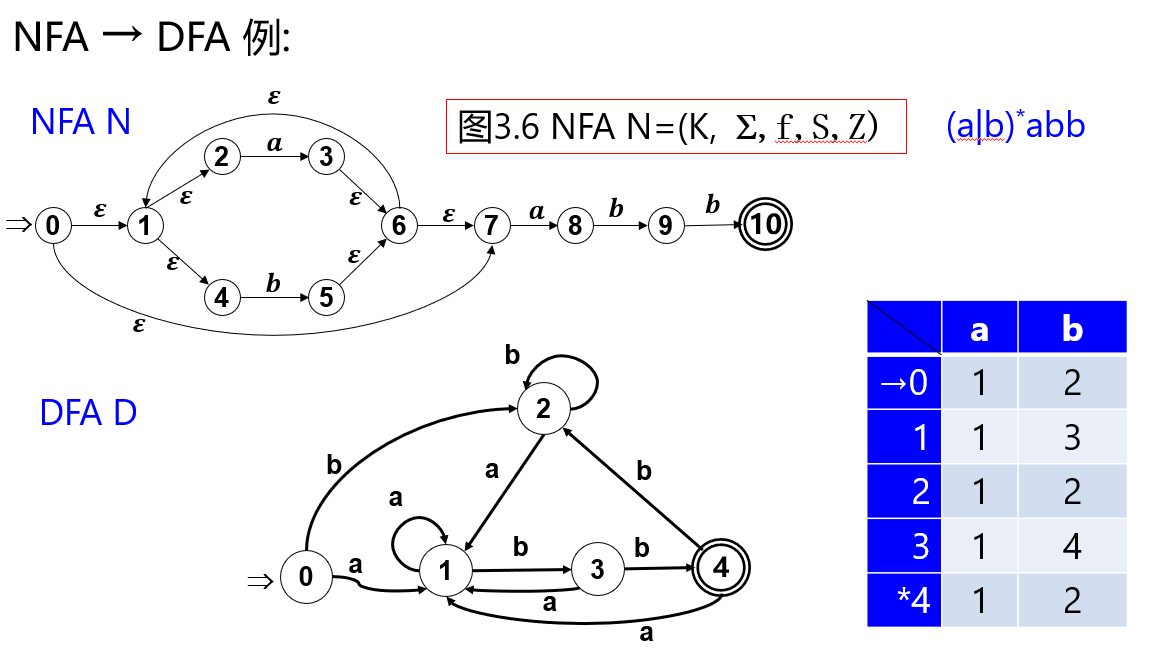
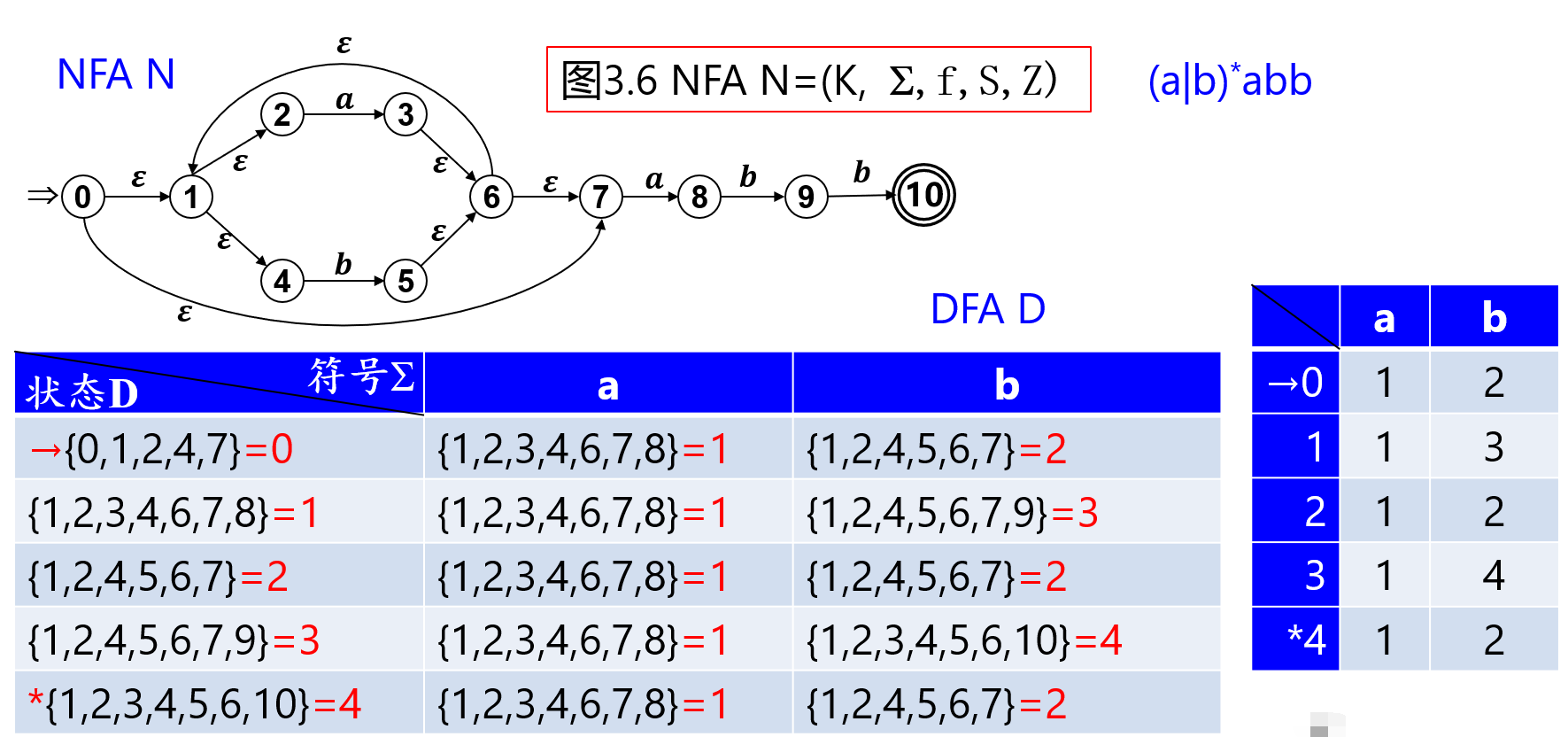
DFA的化简
消除无用状态;无用状态是指不可达,没有通路到达终态。
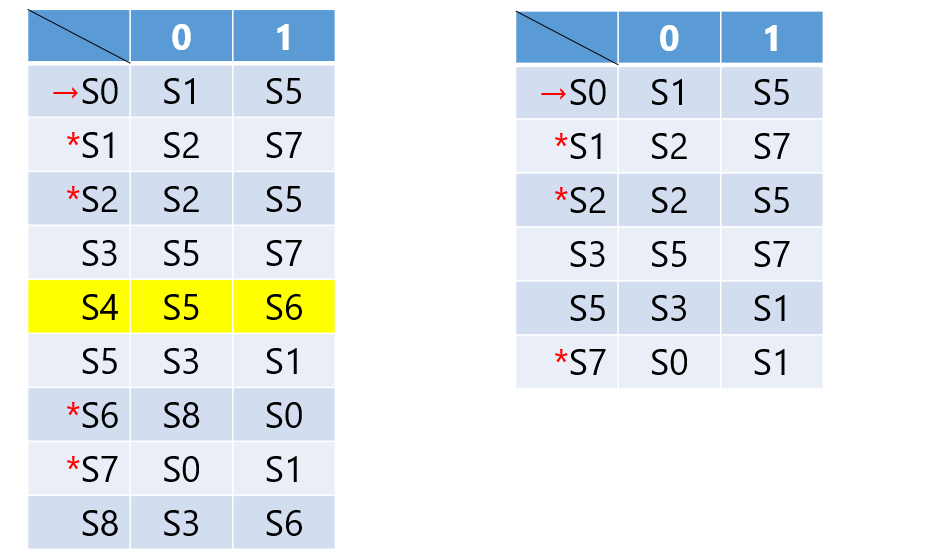
合并等价状态:
- 一致性条件:和同时是可接受状态或不可接受状态
- 蔓延性条件:对所有输入符号,和必须转移到等价的状态中。
方法:分割法——状态被分成不同子集,不同的子集不等价,同一子集等价
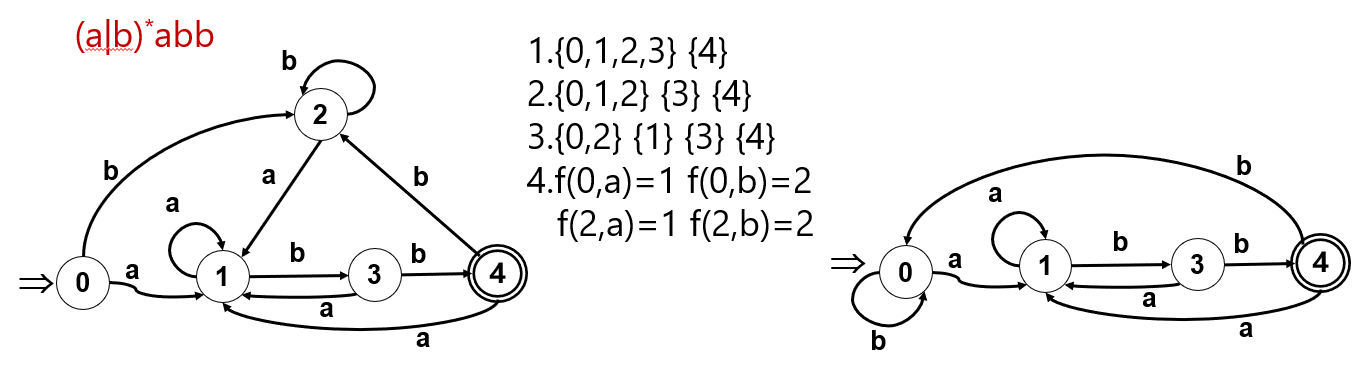
DFA最小化:

正规式和有穷自动机的等价性
对于上的NFA M,可以构造一个上的正规式,使得。
对于上的每一个正规式,可以构造一个上的NFA M,使得
NFA M 正规式
,对的状态转移图进行以下改造:
-
新增两个状态,作为开始状态和接受状态,且将经指向的所有开始状态,将的所有接受状态经指向,得到,显然有。
-
反复使用下面的三条规则,逐步消去结点,直到只剩下为止。到的弧上标记的符号串,即为上等价的正规式。
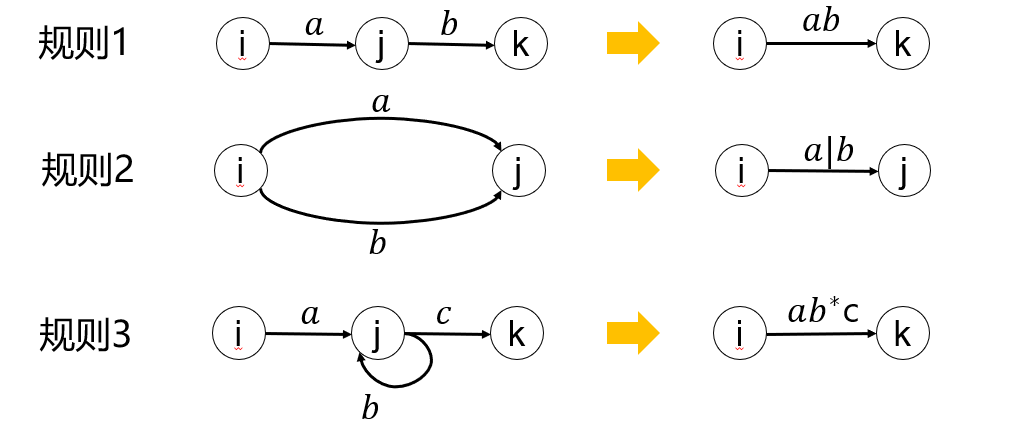
正规式 NFA M
-
首先把表示成:
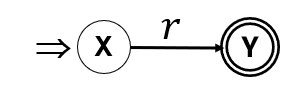
-
按下面的规则对进行分裂:
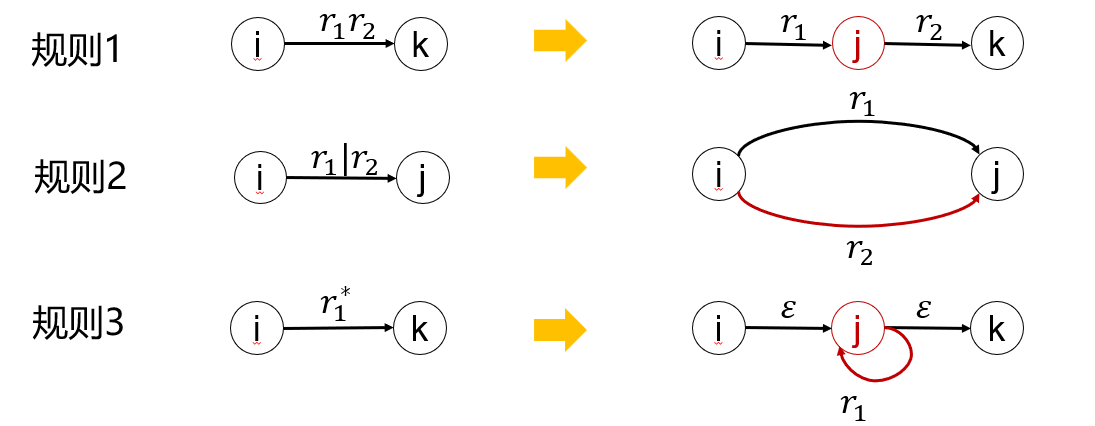
-
直到每条弧上只剩单个符号。
【例】
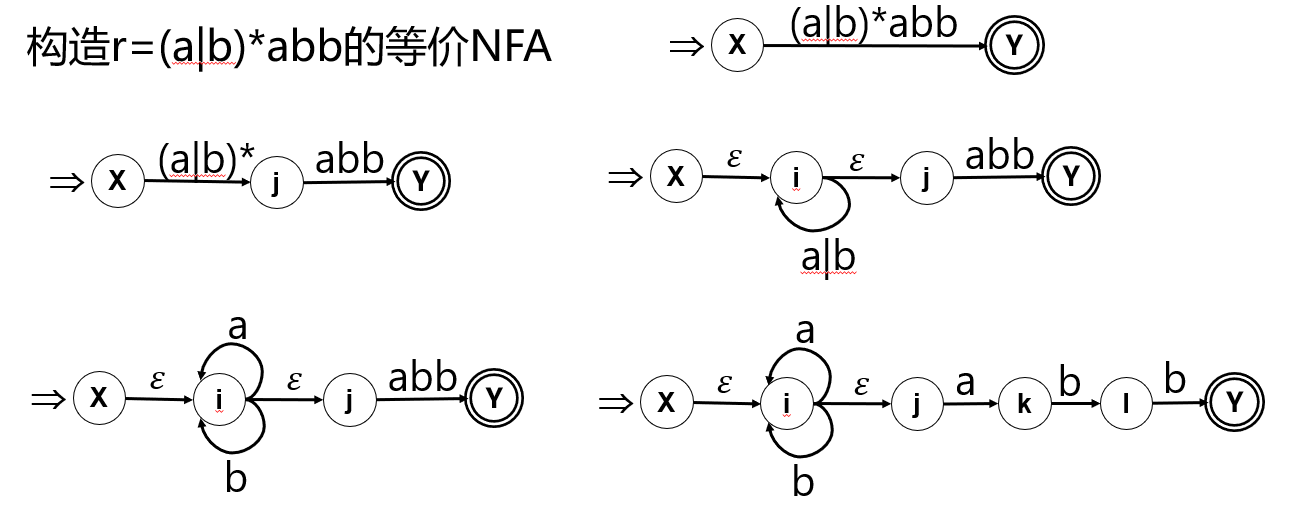
正规文法和有穷自动机的转换
- 正规文法,使得。
- 正规文法,使得。
正规文法 NFA M
- 设
- 的字母表;
- 的每个非终结符是的一个状态;
- 的开始符是的开始状态;
- 增加一个新状态,作为的终态;
- 的状态转移函数:
- 如果;
- 如果;
- 如果;
【例】
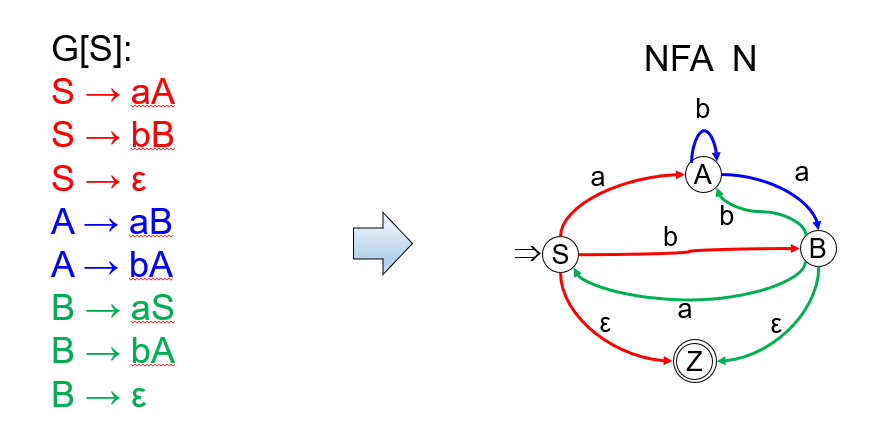
NFAM
有穷自动机正则文法
- 必要时确定化(如果含有转移)
- 的产生式由下列方法构造:
- 如果;
- 对可接受态,增加产生式;
- 如果,为终态且非始态又无出边,可直接。
【例】
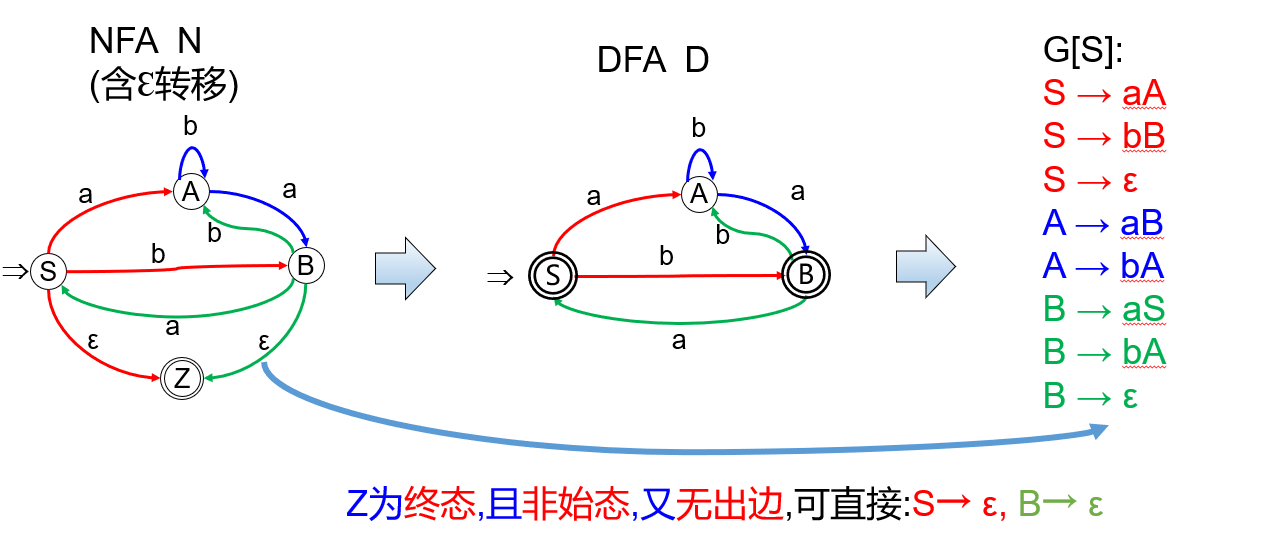
作者:cherish.
出处:https://home.cnblogs.com/u/cherish-/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!