第二章 文法和语言

作者：@cherish.
课程学习内容为作者从学校的PPT处摘抄，仅供自己学习参考，若需转载请注明出处：https://www.cnblogs.com/cherish-/p/16370380.html

---

文法和语言

符号和符号串

• 字母表：字母表$\sum$是非空有穷集合，其元素称为符号。

• 符号串：由字母表$\sum$中的符号组成的有穷序列称为（字母表$\sum$上的）符号串。不含任何符号的有穷序列称为空串，记为$\varepsilon$。

• 规则：以某种形式表达的在一定范围内共同遵守的章程和制度；这里指符号串的组成规则。

  例如：设字母表$\sum = \{0 , 1\}$，则$101$是$\sum$上的符号串，$201$不是$\sum$上的符号串。

• 符号串长度：符号串$\alpha$的长度是指符号串$\alpha$中含有符号的个数，记为$|\alpha|$。特别约定空串$\varepsilon$为零，即$|\varepsilon| = 0$。

• 符号串集合：如果集合$A$的元素都是字母表$\sum$上的符号串，则称集合$A$为$\sum$上的符号串集合，简称串集。

  例如：设字母表$\sum = \{a , b , c\} , A = \{\varepsilon , a , ba , cab\} , B = {a1 , ba , cab}$，则$A$是$\sum$上的符号串集合，$B$不是$\sum$上的符号串集合。

运算

• 符号串的运算：

  设$\alpha , \beta$为两个符号串，则：

  • 连接:$\alpha \cdot \beta= \alpha\beta$，如$a \cdot b = ab$

  • 或：$\alpha | \beta = \alpha 或者\beta$

  • 方幂：$\alpha ^n = \alpha\alpha...\alpha = \alpha\alpha ^{n - 1} = \alpha^{n - 1}\alpha$。注意：$\alpha ^ 0 = \varepsilon$。

  • 闭包：$\alpha^1 = \alpha , \alpha^2 = \alpha\alpha ,...$

    $\alpha$的正闭包：$\alpha^+= \alpha^1|\alpha^2|...|\alpha^n|...$

    $\alpha$的星闭包：$\alpha^*=\alpha^0|\alpha^1|\alpha^2...|\alpha^n|...$

• 符号串集合的运算：

  设$A , B$为两个符号串集合，则：

  • 乘积：$AB = \{xy | x \in A \;and\; y \in B \}$

  • 和：$A \cup B = A + B = \{x | x \in A \;or\;x \in B\}$

  • 方幂：$A^n = AA...A = AA^{n - 1} = A^{n - 1}A$。注意：$A^0 = \{\varepsilon\}$。

  • 闭包：

    $A$的正闭包：$A^+ = A^1\cup A^2\cup ... \cup A^n \cup...$

    $A$的星闭包：$A* = A^0 \cup A^1\cup A^2\cup ... \cup A^n \cup...$

  • 推论：若$A$为任一字母表，则$A^*$就是该字母表上的所有符号串（包括空串）的集合。

文法和语言的形式化定义

什么是“形式化定义”？

• 对文法的一种精确的数学定义
• 定义的“文法”，“句子”等概念，虽然可以和自然语言的对应概念类比，但它们有严格的数学基础，可以被计算机处理。

文法的形式化定义包含哪些内容？

• 文法的生成规则（<主语> := <名词>|<代词>）
• 文法使用的非终结符（代词）
• 文法使用的终结符
• 文法的开始符号

定义：文法$G$定义为一个四元组$(V_N , V_T , P , S)$，记为$G = (V_N , V_T , P , S)$。其中：

• $V_N$是非空有穷集合，称为非终结符集，其元素称为非终结符；
• $V_T$是有穷集合，称为终结符集，其元素称为终结符；
• $P$是非空有穷集合，称为规则集，其元素是字母表$V_N \cup V_T$上的规则，$V_N \cup V_T$称为文法的字母表$V$，且$V_N \cap V_T = \empty$；
• $S \in V_N$，称为开始符。

字母表$V$上的规则：（重写规则、产生式、生成式）

$\alpha ::= \beta$简记为$\alpha \to \beta$。$\alpha \in V^+$规则的左部，$\beta \in V^*$称为规则的右部。

$\alpha \to \varepsilon$是空规则

左部相同的多个规则，可以使用符号$|$简写。如：

• $\alpha \to \beta$
• $\alpha \to \delta$ 可简写为$\alpha \to \beta | \delta$。

【例】定义文法$G$如下：$G = (V_N , V_T , P , S)$，其中：$V_N = \{S\} , V_T =\{a , b\} , P = \{S\to aSb , S\to ab\}$。

上式亦可写成如下形式：

• $G = (\{S\} , \{a , b\} , P , S) , P = \{S\to aSb , S\to ab\}$
• $G = (\{S\} , \{a , b\} , \{S\to aSb , S\to ab\} , S)$
• $G[S]: S\to aSb , S\to ab$

【例】：文法$G$定义如下：$G= (V_N , V_T , P , S),V_N = \{S\} , V_T = \{0 , 1\},P = \{S\to 0S1 , S\to 01\}$

这个文法表达的语言是什么？$L = \{0^n1^n | n \geq 1\}$。

直接推导

设文法$G = (V_N , V_T , P , S)$，如果$P$中包含$\alpha \to \beta$，那么任意的串$\gamma\alpha\delta$可以推导出$\gamma\beta\delta$，我们把这种推导称为直接推导或一步推导，记为$\gamma\alpha\delta \Rightarrow \gamma\beta\delta$。$Note:\gamma , \delta \in V^*$。

直接规约

如果$\gamma\alpha\delta \Rightarrow \gamma\beta\delta$，我们也可以说$\gamma\beta\delta$规约 到$\gamma\alpha\delta$，这种规约称为直接归约或一步归约。

多步推导

设文法$G = (V_N , V_T , P , S)$，对于$\alpha , \beta \in V^* = (V_N \cup V_T)^*$，如果$\alpha , \beta$之间存在一个推导序列：$\alpha = \omega_0 \Rightarrow \omega_1 \Rightarrow ... \Rightarrow \omega_n = \beta(n \geq 1)$，则称$\alpha$经过$n$步推导出$\beta$，记作$\alpha \stackrel{+}{\Rightarrow} \beta$，这种推导称为多步推导或$n$步推导。$Note:\omega_i \in V^* \forall 1 \leq i \leq n$。

多步规约

如果$\alpha \stackrel{+}{\Rightarrow} \beta$，也称$\beta$规约到$\alpha$，也称为$n$步归约或多步归约。

$0$步及$0$步以上推导与规约：若有$\alpha \stackrel{+}{\Rightarrow} \beta$,或$\alpha \to \beta$，则记作$\alpha \stackrel{*}{\Rightarrow} \beta$。

句型与句子

• $G[S]$有$S \stackrel{*}{\Rightarrow} \beta$，则称$\beta$是文法$G[S]$的句型。
• 若$\beta \in V_T^*$，则称$\beta$是文法$G$的句子。

语言

文法$G = (V_N , V_T , P , S)$的产生语言定义为文法$G$的句子集合，记为$L(G)$。即：$L(G) = \{\beta | S \stackrel{*}{\Rightarrow} \beta , \beta \in V_T^*\}$。

【例】：$G[S]: S\to aSb , S\to ab$，则$L(G) = \{a^nb^n|n \geq 1\}$。

文法的等价

文法$G_1 , G_2$，如果$L(G_1) = L(G_2)$，则称文法$G_1$和$G_2$是等价的。

【例】:

$G1 = (\{S , C\} , \{a , d\} , P , S), P = \{S \to aC , C \to aC , C \to dC , C \to \varepsilon\}$

$G2 = (\{S\} , \{a , d\} , P , S), P = \{S \to Sa , S \to Sd , S \to a\}$

显然有$L(G_1) = L(G_2) = \{a(a|d)^*\}$。

文法的类型

0型文法

• 如果一个文法的所有规则左侧至少含有一个非终结符，则称此文法为$0$型文法，也称为短语文法。
• 产生式形如：$\alpha \to \beta$，其中$\alpha \in (V_T \cup V_N)^+$且至少含有一个非终结符；$\beta \in (V_T \cup V_N)^*$。

1型文法

• 如果一个文法的所有规则左侧符号串的长度不大于右侧符号串的长度（空规则除外），且左侧至少含有一个非终结符，则称此文法为$1$型文法，也称为上下文相关文法。
• 产生式形如：$\alpha \to \beta$，其中$|\alpha| \leq |\beta|$，仅$S \to \varepsilon$例外。
• 考虑$\gamma A\delta \Rightarrow \gamma\beta\theta\delta$，$A$被替换成$\beta\theta$，跟$A$的上下文相关。

2型文法

• $\forall\; \alpha \to \beta \in P , \alpha \in V_N$，则文法是$2$型文法，也称为上下文无关文法。$\beta \in (V_T \cup V_N)^*$。（即任一产生式左部均为一非终结符。）

3型文法

文法$(N , \sum , P , S)$的产生式只能是以下两者之一：

• $A \to \varepsilon | a | aB \;\;A , B \in V_N , a \in V_T$——右线性文法
• $A \to \varepsilon | a | Ba \;\;A , B \in V_N , a \in V_T$——左线性文法

统称$3$型文法，又叫正则文法。

【例】：文法$G = (V_N , V_T , P , S)$是正则文法，$V_N = \{S , A , B\} , V_T = \{0 , 1\} , P = \{S \to A0 | B1 , A \to 0 | 1 , B \to 0 | 1\}$。

则$L(G) = \{00 , 01 , 10 , 11\}$。

文法的类型于表达能力

• 从$0$型文法到$3$型文法，限制逐渐增多，表达能力也逐渐减弱
• 如果$L_0 , L_1 , L_2$和$L_3$分别是$0$型文法、$1$型文法、$2$型文法和$3$型文法能产生的语言之集，则有如下关系：$L_0 \supseteq L_1 \supseteq L_2 \supseteq L_3$。

上下文无关文法及其语法树

• 上下文无关文法—描述程序语言的语法结构

  【例】$G[E] : E \to i | E + E | E * E | (E)$

• 从一个句型到另一个句型的推导往往不唯一

  如：$E + E \Rightarrow i + E \Rightarrow i + i , E + E \Rightarrow E + i \Rightarrow i + i$。

• 最左推导：任何一步$\alpha \Rightarrow \beta$都是对$\alpha$中的最左非终结符进行替换

• 最右推导：任何一步$\alpha \Rightarrow \beta$都是对$\alpha$中的最右非终结符进行替换

• 最右推导，也叫做规范推导。由规范推导所得到的句型，叫做规范句型（右句型）。规范推导的逆过程，叫做规范归约。

【例】 最左/最右推导过程示例

已知文法如下，试给出句子aabbaa的推导过程。

$G[S]: S \to aAS | a , A\to SbA | SS|ba$

• 最左推导：$S \Rightarrow aAS \Rightarrow aSbAS \Rightarrow aabAS \Rightarrow aabbaS \Rightarrow aabbaa$
• 最右推导：$S \Rightarrow aAS \Rightarrow aAa \Rightarrow aSbAa \Rightarrow aSbbaa \Rightarrow aabbaa$

语法树

文法$G$的任何一个句型，根据其推导都能构造一个语法树，也称为推导树。它是一个满足下列条件的多叉树：

• 文法的开始符$S$为树的根节点
• 对任一产生式$A \to \alpha , \alpha \in (V_N \cup V_T)^*$，$\alpha$的各符号严格依生产式的次序依次为$A$的子节点；文法符号为其节点标记（节点名）。

【例】 语法树示例

已知文法如下，试给出句子aabbaa的推导过程。

$G[S]: S \to aAS | a , A\to SbA | SS|ba$

• 最左推导：$S \Rightarrow aAS \Rightarrow aSbAS \Rightarrow aabAS \Rightarrow aabbaS \Rightarrow aabbaa$
• 最右推导：$S \Rightarrow aAS \Rightarrow aAa \Rightarrow aSbAa \Rightarrow aSbbaa \Rightarrow aabbaa$

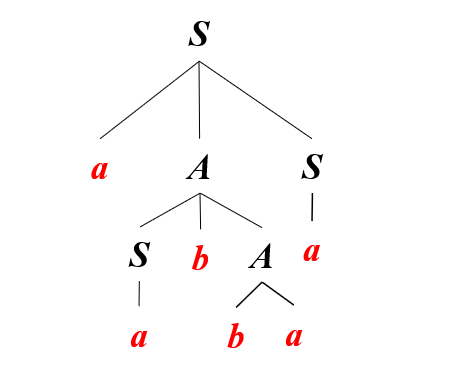
结论：

• 非叶子结点一定是非终结符
• 全部叶子结点组成的符号串是文法的句子

语法树的二义性

• 如果文法$G$的某个句子存在至少两棵不同的语法树，则称该文法$G$是二义的。
• 如果文法是无二义性的，一个句子的语法树反映了该句子的全部推导过程。
• 如果文法是无二义性的，一个句子的最左（最右）推导是唯一的。

【例】语法二义性示例

已知文法$G[E] : E \to E + E | E*E|(E)|i$，证明$G$是二义的。

证明：因为句子$i + i * i$存在下列两棵不同的语法树

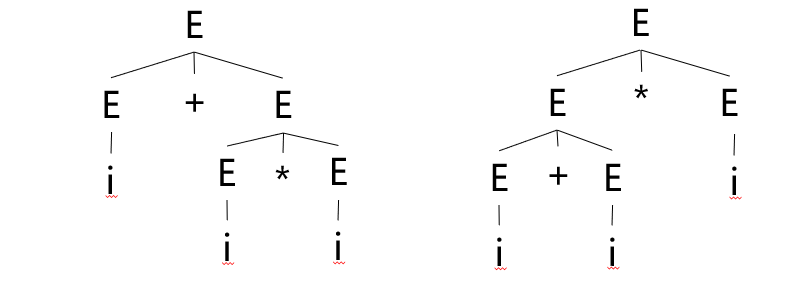
故文法$G[E]$是二义性的文法。

语言的二义性

• 文法的二义性并不等同于语言的二义性。
• 因为二义性文法$G$，可能存在与之等价的无二性的文法$G^{'}$，即$L(G) = L(G^{'})$。
• 如果一个语言不存在无二义性的文法，则称该语言是先天二义性的。
• 二义性问题是不可判定问题，即不存在一个算法，它能在有限步骤内，确切地判定一个文法是否是二义的。

句型的分析

• 假设文法$G[S]$是语言$L$之文法，即$L(G) = L$，则“符号串$\alpha$ 是否符合语言$L$的语法问题”被等价地转化成“推导或归约问题”，即：

  $$S\stackrel{*}{\Rightarrow} \alpha\;\land\;\alpha \in V_T^*$$

• 推导法 VS 归约法

• 自顶向下 VS 自底向上

• Antlr VS Bison

  自顶向下分析

• 从文法开始符号出发，反复使用规则，寻找匹配符号串（推导）的句型，直到推导出句子或穷尽规则也不能推导出。进行每一步推导时，存在两个选择问题：

  • 选择句型中那一个非终结符进行推导
  • 选择非终结符的那一个规则进行推导

• 最左推导，穷举规则：

  • 推导过程中一旦出现符号串$\alpha$：$\alpha$是合法的句子。
  • 穷尽规则，不存在$\alpha$的推导过程：$\alpha$不是合法的句子。

【例】 串$w = cabd$的推导过程

设文法$G[S]: S\to cAd\;\;A\to a|ab$

序号	推导过程	串	说明
1	$S$	cabd
2	$S \Rightarrow cAd$	caba	$r_1$匹配$c$
3	$S\Rightarrow cad$	cabd	$r_2$，失败，回溯
4	$S\Rightarrow cAd$	cabd	$r_3$
5	$S \Rightarrow cabd$	cabd	成功

$Note:r_i$表示第$i$个规则。

回溯的效率很低，改进办法——提取公因子，原文法转化为：

$G[S^{'}] : S \to cAd\;A \to aA^{'}\;A^{'} \to b\;A^{'} \to \varepsilon$

分析目标：$w = cabd$：

$$S \Rightarrow cAd \Rightarrow caA^{'}d \Rightarrow cabd$$

自下而上的分析法

• 从输入符号串$\alpha$开始，逐步进行归约，直至归约出文法的开始符号$S$，则输入串$\alpha$是文法$G$定义的句子，否则不是。
  • 归约是推导的逆过程
  • 每步归约时，存在如何选择句型$\alpha$的子串$\beta$进行归约的问题$(\alpha = \beta \delta)$。
• 方案：按句柄归约—规范归约（移进—归约）
  • 简单优先分析法
  • LR分析法

【例】：$G[S]:S\to cAd , A\to a , A \to ab$，分析目标：$w = cabd$

短语、直接短语、句柄

设文法$G[S]$有：$S \stackrel{*}{\Rightarrow } \alpha A \delta \stackrel{*}{\Rightarrow }\alpha \beta\delta$，且$A \stackrel{*}{\Rightarrow } \beta$。

• $\beta$是句型$\alpha \beta\delta$相对于非终结符$A$的短语。任一子树的树叶全体（具有共同祖先的叶结点符号串）皆为短语；
• 特别地，$S \stackrel{*}{\Rightarrow } \alpha A \delta \stackrel{}{\Rightarrow }\alpha \beta\delta$，即$A \stackrel{}{\Rightarrow } \beta$，则$\beta$是句型$\alpha \beta\delta$相对于规则$A \to \beta$的直接短语（简单短语）。任一简单子树的树叶全体（具有共同父亲的叶节点符号串）皆为简单短语；
• 右句型的最左直接短语称为该句型的句柄。

【例】：文法$G[E]: E \to E + T | T , T\to T*F |F , F\to (E)|i$，分析句型$i_1 + i_2 * i_3$的短语、直接短语或句柄。

$$E \Rightarrow E + T \Rightarrow E + T * F \Rightarrow E + T * i_3 \Rightarrow E + F * i_3 \Rightarrow E + i_2 * i_3\Rightarrow T + i_2 * i_3 \Rightarrow F + i_2 * i_3 \Rightarrow i_1+ i_2 * i_3$$

• $i_3$是句型$E + T * i_3$的、相对于非终结符$F$的直接短语
• $i_2$是句型$E + i_2 * i_3$的、相对于非终结符$T$的短语，$F$的直接短语
• $i_1$是句型$i_1 + i_2 * i_3$的、相对于非终结符$F$的短语、直接短语和句柄

对于上述文法，分析句型$i_1 + i_2 * i_3$的语法树如下：

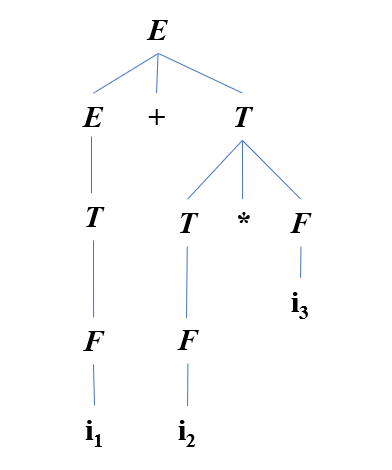
短语：$i_1 , i_2 , i_3 , i_2*i_3 , i_1 + i_2 * i_3$

直接短语：$i_1 , i_2 , i_3$

句柄：$i_1$

补充说明

• 文法不得含有有害规则，多余规则
  • 有害规则：$A \to A$
  • 不可达（用）规则：不在任何产生式右部出现的非终结符及其规则
  • 不可终止规则：从某非终结符开始，不可能推导出任意终结符串来。
• 对文法$G$中的符号$X$是有用的，是指$X$至少出现在一个句子的推导过程中，即$X$必须同时满足以下两个条件：
  • $X$必须在某个句型中出现，即存在$\alpha,\beta \in V^*$有$S \stackrel{*}{ \Rightarrow } \alpha X \beta$（可达）
  • 必须能够从$X$推导出终结符号串，即存在$w \in V_T^*$，使$\alpha X \beta \stackrel{*}{ \Rightarrow} w$（可终结）
• 含有无用符号的产生式称为无用产生式

文法化简

对于文法$G = (V_N , V_T , P , S)$

• 删除不终结产生式算法：（满足条件2-可终结）

  • 构造能推导出终结符号串的非终结符集$V_{N1}$，置$V_{N1} = \empty$；

    1. 对$P$中每一个产生式$A \to \alpha$，若$\alpha \in V_T^*$；则$V_{N1} \cup= A$；

    2. 对$P$中的每一个产生式$B \to \beta$，若$\beta \in (V_T \cup V_{N1})^*$，则$V_{N1} \cup = B$

    3. 重复步骤2直到$V_{N1}$不再扩大为止。

  • 删除不在$V_{N1}$中的所有非终结符的相关产生式。

  • $G = (V_{N1} , V_T , P_1 , S)$

• 删除不可用产生式算法：（满足条件1-可达）

  • 初始化：$V_{N2} = {S} , V_{T2} = \empty , P_2 = \empty$
    1. 对每一个产生式$A \to \alpha$，若$A \in V_{N2}$，则将$\alpha$中的非终结符并入$V_{N2}$，终结符并入$V_{T2}$；
    2. 重复步骤1，直到$V_{N2}$和$V_{T2}$都不再扩大为止；
    3. 将$P$中左右部仅含$V_{N2} \cup V_{T2}$中的符号的所有产生式并入$P_2$中。
  • $G = (V_{N2} , V_{T2} , P_2 , S)$

epsilon($\varepsilon$)规则

• 在文法设计中，$\varepsilon$规则带来方便，也导致文法讨论和证明的复杂性
• 一个上下文无关文法$G$是否必须使用$\varepsilon$规则，完全取决于文法$G$产生的语言$L(G[S])$中是否含有$\varepsilon$语句。
• 可以证明，如果$\varepsilon \not\in L(G[S])$，则存在一个等价的文法$G^{'}[S^{'}]$，且$G^{'}$不含$\varepsilon$规则。
• 如果$\varepsilon \in L(G[S])$，则存在一个等价的文法$G^{'}[S^{'}]$，且$G^{'}$仅含$S^{'} \to \varepsilon$的一个空规则。
• 设文法$G[S]$，$\varepsilon \not\in L(G)$，消除$\varepsilon$规则：
  • 首先构造出可以推出空串的非终结符集：$V_{\varepsilon}$
    1. 若有$A \to \varepsilon$；则令$V_{\varepsilon} \cup=A$；
    2. 若有$B \to A_1...A_n$且全部$A_i \in V_{\varepsilon}$，则令$V_{\varepsilon} \cup = B$；
    3. 重复步骤1，2直到$V_{\varepsilon}$不再扩大为止。
  • 删除$G[S]$中的$A \to \varepsilon$形式的产生式；
  • 依次改写$G[S]$中的产生式$B \to X_1...X_n$；若有$X_i \in V_{\varepsilon}$,则用$\{X_i| \varepsilon\}$替换之（一个分裂成两个）；
  • 若有$j$个$X_i \in V_{\varepsilon}$，则一个产生式将分裂成$2^j$个。

【例题】