流水技术

流水线的基本概念

什么是流水线

工业生成流水线
流水线技术：把一个重复的过程分解为若干个子过程，每个子过程由专门的功能部件来实现；把多个处理过程在时间上错开，依次通过各功能段，这样，每个子过程就可以与其它的子过程并行进行。
流水线中的每个子过程及其功能部件称为流水线的级或段，段与段相互连接形成流水线。流水线的段数称为流水线的深度。
指令流水线：把指令的解释过程分解为分析和执行两个子过程，并让这两个子过程分别用独立的分析部件和执行部件来实现。理想情况下速度提高一倍。

4段指令流水线示意图：
浮点加法流水线：把流水线技术应用于运算的执行过程，就形成了运算操作流水线，也称为部件级流水线；把浮点加法的全过程分解为求阶差、对阶、尾数、相加、规格化四个子过程。理想情况下速度提高3倍。
时-空图：时-空图从时间和空间两个方面描述了流水线的工作过程。同一时-空图中，横坐标代表时间，纵坐标代表流水线的各个段，下给出浮点加法流水线的时空图。
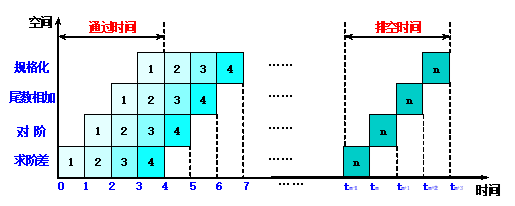
流水技术的特点：
- 流水线把一个处理过程分解为若干个子过程（段），每个子过程由一个专门的功能部件来实现；
- 流水线中各段的时间应尽可能相等，否则将引起流水线堵塞、断流，时间最长的段将成为流水线的瓶颈；
- 流水线每一个段的后面都要有一个缓冲寄存器（锁存器），称为流水寄存器，其作用是在相邻的两段之间传送数据，以保证提供后面要用到的信息，并把各段的处理工作相互隔离。
- 流水技术适合与大量重复的时序过程，只有在输入端不断地提供任务，才能充分发挥流水线的效率。
- 流水线需要有通过时间和排空时间：通过时间：第一个任务从进入流水线到流出结果所需要的时间；排空时间：最后一个任务从进入流水线到流出结果所需的时间。

流水线的分类

部件级、处理机级及处理机间流水线——按照流水技术用于计算机系统的等级不同
- 部件级流水线（运算操作流水线）：把处理机中的部件分段，再把这些分段相互连接起来，使得各种类型的运算操作能够按流水方式进行。
- 处理机级流水线（指令流水线）：把指令的执行过程按照流水方式处理。把一条指令的执行过程分解为若干个子过程，每个子过程在独立的功能部件中执行。
- 系统级流水线（宏流水线）：把多台处理机串行连接起来，对同一数据流进行处理，每个处理机完成整个任务中的一部分。
单功能流水线与多功能流水线——按照流水线所完成的功能来分类
- 单功能流水线：只能完成一种固定功能的流水线。
- 多功能流水线：流水线的各阶段可以进行不同的连接，以实现不同的功能。
静态流水线与动态流水线——按照同一时间内各段之间的连接方式对多功能流水线作进一步的分类
- 静态流水线：在同一时间内，多功能流水线中的各段只能按同一种功能的连接方式工作。对于静态流水线来说，只有当输入的是一串相同的运算任务时，流水的效率才能得到充分的发挥。
- 动态流水线：在同一时间内，多功能流水线中的各段可以按照不同的方式连接，同时执行多种功能。优点：灵活，能够提高流水线各段的使用率，从而提高处理速度。缺点：控制复杂。
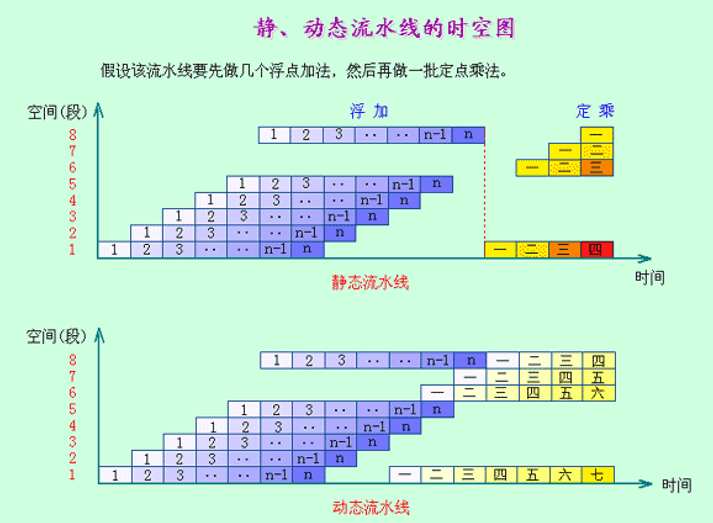
线性流水线与非线性流水线——按照流水线中是否有反馈回路来进行分类
- 线性流水线：流水线的各段串行连接，没有反馈回路。数据通过流水线中的各段时，每一个段最多只流过一次。
- 非线性流水线：流水线中除了有串行的连接外，还有反馈回路。
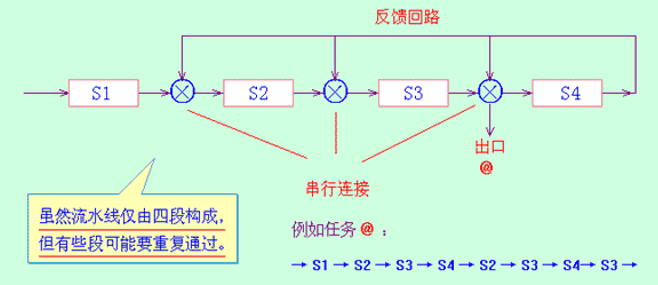
顺序流水线与乱序流水线——根据任务流水和流出顺序是否相同来进行分类
- 顺序流水线：流水线输出端任务流出的顺序与输入端任务流入的顺序完全相同。每一个任务在流水线的各段中是一个跟着一个顺序流动的。
- 乱序流水线：流水线输出端任务流出顺序与输入端任务流入的顺序可以不同，允许后进入流水线的任务先完成。也称为无序流水线、错序流水线、异步流水线。
标量处理机与向量流水处理机
- 把指令执行部件中采用了流水线的处理机称为流水线处理机。
- 标量处理机：处理机不具有向量数据表示和向量指令，仅对标量数据进行流水处理。
- 向量流水处理机：具有向量数据表示和向量指令的处理机。向量数据表示和流水技术的结合。

流水线的性能指标

吞吐率

吞吐率：在单位时间内流水线所完成的任务数量或输出结果的数量\(TP = \frac{n}{T_k}\)，其中\(n\)表示任务数量；\(T_k\)表示处理完\(n\)个任务所用的时间。

各段时间均相等的流水线

各段时间均相等的流水线时空图
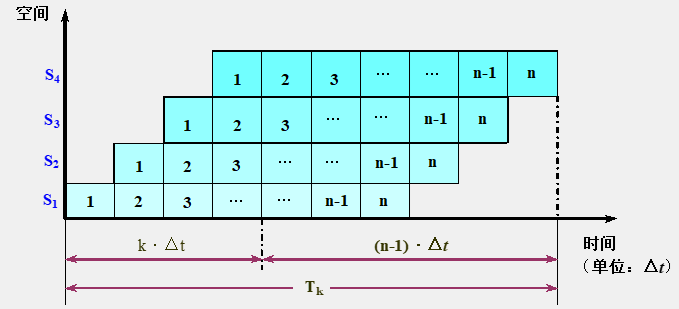
流水线完成\(n\)个连续任务所需要的总时间为（假设是一条\(k\)段线性流水线）：

\[T_k = k\Delta t + (n - 1)\Delta t = (k + n - 1)\Delta t \]
流水线的实际吞吐率：

\[TP = \frac{n}{(k + n - 1)\Delta t} \]
最大吞吐率：

\[TP_{max} = \lim\limits_{n \to \infin} \frac{n}{(k + n - 1)\Delta t} = \frac{1}{\Delta t} \]
最大吞吐率与实际吞吐率的关系：

\[TP = \frac{n}{k + n - 1}TP_{max} \]
流水线的实际吞吐率小于最大吞吐率，它除了与每个段的时间有关外，还与流水线的段数\(k\)以及输入到流水线中的任务数\(n\)等有关。只有当\(n \gg k\)时，才有\(TP \approx TP_{max}\)。

各段时间不完全相等的流水线

各段时间不等的流水线及其时空图
- 举例1如下；一条4段的流水线；\(S_1\)，\(S_2\)，\(S_3\)各段的时间为\(\Delta t\);\(S_2\)的时间为\(3\Delta t\)（瓶颈段）；流水线中这种时间最长的段称为流水线的瓶颈段。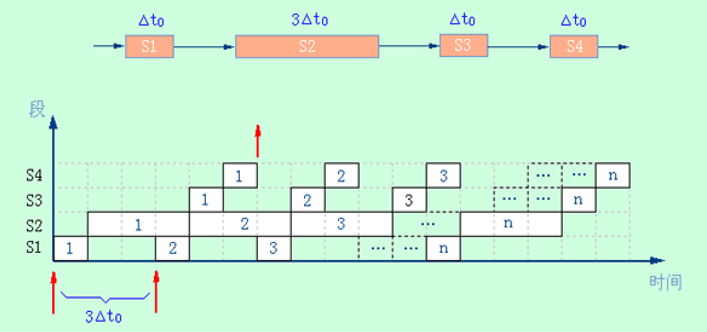
- 举例2：\(S_1\)，\(S_2\)，\(S_3\)，\(S_5\)各段的时间为\(\Delta t\)；\(S_4\)的时间为\(3\Delta t\)（瓶颈段）
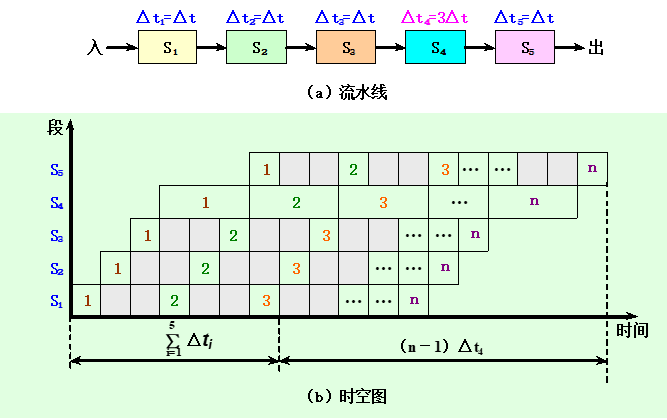
各段时间不等的流水线的实际吞吐率为（\(\Delta t_i\)表示第\(i\)段的时间，共\(k\)个段）：

\[TP = \frac{n}{\sum\limits_{i = 1}^{k}\Delta t_i + (n - 1)\mathop{max}(\Delta t_1 , \Delta t_2 , ... , \Delta t_k)} \]
流水线的最大吞吐率为：

\[TP_{max} = \frac{1}{\mathop{max}(\Delta t_1 , \Delta t_2 , ... , \Delta t_k)} \]
对于前面举例2中的5段流水线，其最大吞吐率为\(TP_{max} = \frac{1}{3\Delta t}\)。

解决流水线瓶颈问题的常用方法

细分瓶颈段

例如：对于举例2中的5段流水线，把瓶颈段\(S_4\)细分为3个字流水线段：\(S_{4-1}\)，\(S_{4-2}\)，\(S_{4-3}\)，改进后的流水线的吞吐率为：\(TP_{max} = \frac{1}{\Delta t}\)。
重复设置瓶颈段（缺点：控制逻辑比较复杂，所需的硬件增加了）

例如：对于举例2中的5段流水线，重复设置瓶颈段\(S_4\)：\(S_{4a}\)，\(S_{4b}\)，\(S_{4c}\)，其示意图和时空图如下：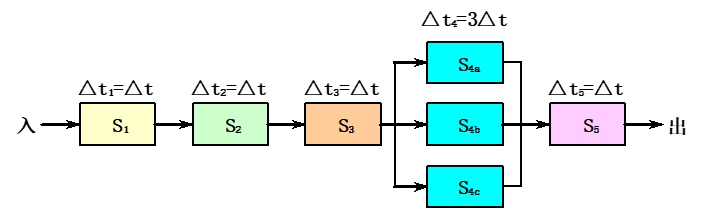

流水线的加速比

加速比：完成同样的一批任务，不使用流水线所用的时间与使用流水线所用的时间之比。假设：不使用流水线（即顺序执行）所用的时间为\(T_s\)，使用流水线后所用的时间为\(T_k\)，则该流水线的加速比为：

\[S = \frac{T_s}{T_k} \]

流水线各段时间相等

都是\(\Delta t\)

一条\(k\)段流水线完成\(n\)个连续任务所需的时间为：

\[T_k = (k + n - 1)\Delta t \]
顺序执行\(n\)个任务所需要的时间为：

\[T_s = nk\Delta t \]
流水线的实际加速比为：

\[S = \frac{nk}{k + n - 1} \]
最大加速比：

\[S_{max} = \lim\limits_{n \to \infin} \frac{nk}{k + n - 1} = k \]
即当\(n \gg k\)时，\(S \approx k\) 。

流水线的各段时间不完全相等时

一条\(k\)段流水线完成\(n\)个连续任务的实际加速比为：
\[S = \frac{n\sum\limits_{i = 1}^{k}\Delta t_i}{\sum\limits_{i = 1}^{k}\Delta t_i + (n - 1)\mathop{max}(\Delta t_1 , \Delta t_2 , ...,\Delta t_k)} \]

流水线的效率

定义：流水线中的设备实际使用时间与整个运行时间的比值，即流水线设备的利用率。

由于流水线有通过时间和排空时间，所以在连续完成\(n\)个任务的时间内，各段并不是满负荷地工作。

各段时间相等

各段的效率\(e_i\)相同：

\[e_1 = e_2 = ...=e_k = \frac{n\Delta t}{T_k} = \frac{n}{k + n - 1} \]
整条流水线的效率为：

\[E = \frac{e_1 + e_2 + ... + e_k}{k} = \frac{ke_1}{k} = \frac{kn\Delta t}{kT_k} = \frac{n}{n + k - 1} \]
最高效率为：

\[E_{max} = \lim\limits_{n \to \infin}\frac{n}{k + n - 1} = 1 \]
当\(n \gg k\)时，\(E \approx 1\)。
当流水线各段时间相等时，流水线的效率与吞吐率成正比：

\[E = TP \times \Delta t \]

流水线的效率是流水线的实际加速比\(S\)与它的最大加速比\(k\)的比值，即：

\[E = \frac{S}{k} \]

当\(E = 1\)时，\(S = k\)，实际加速比达到最大。

从时空图上看，效率就是\(n\)个任务占用的时空面积和\(k\)个段总的时空面积之比。即：

\[E = \frac{n个任务实际占用的时空区}{k个段总的时空区} \]

当各段时间不相等时：
\[E = \frac{n\sum\limits_{i = 1}^{k}\Delta t_i}{k[\sum\limits_{i = 1}^{k}\Delta t_i + (n - 1)\mathop{max}(\Delta t_1 , \Delta t_2 , ... , \Delta t_k)]} \]

流水线的性能分析举例

例3.1 设在下图所示的静态流水线上计算：\(\prod\limits_{i = 1}^{4}(A_i + B_i)\)。流水线的输出可以直接返回输入端或暂存于相应的流水寄存器中，试计算其吞吐率、加速比和效率。（每段的时间都为\(\Delta t\)）

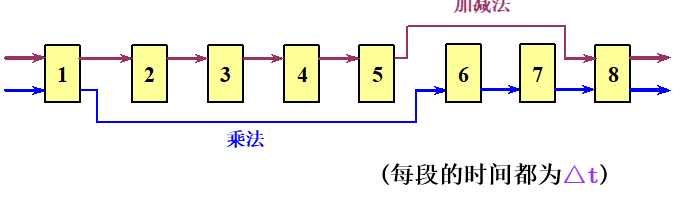
解

选择适合与流水线工作的算法：
- 先计算\(A_1 + B_1\)、\(A_2 + B_2\)、\(A_3 + B_3\)和\(A_4 + B_4\)
- 再计算 \((A_1 + B_1) \times (A_2 + B_2)\)和\((A_3 + B_3) \times (A_4 + B_4)\)
- 最后再计算总的乘积结果
画出时空图
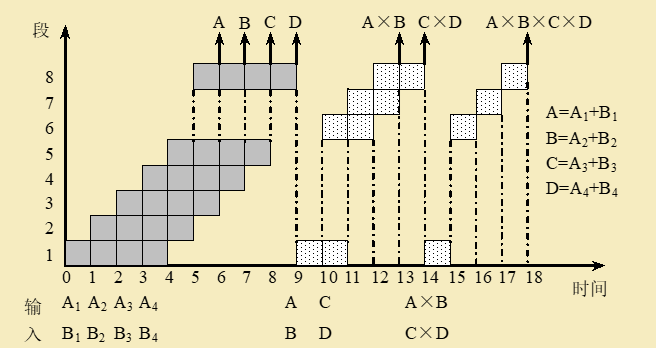
计算性能
- 在\(18\)个\(\Delta t\)时间中，给出了\(7\)个结果，吞吐率为：
  
  \[TP = \frac{7}{18\Delta t} \]
- 不同流水线，由于一次求和需\(6\Delta t\)，一次求积需要\(4\Delta t\)，则产生上述\(7\)个结果共需要\((4 \times 6 + 3 \times 4)\Delta t = 36 \Delta t\)，则加速比为：
  
  \[S = \frac{36\Delta t}{18\Delta t} = 2 \]
- 流水线的效率为：
  
  \[E = \frac{4 \times 6 + 3 \times 4}{8 \times 18} = 0.25 \]
题后分析

可以看出，在求解此问题时，该流水线的效率不高，主要原因如下：
- 多功能流水线在做某一种运算时，总有一些段是空闲的；
- 静态流水线在进行功能切换时，要等前一种运算全部流出流水线后才能进行后面的运算；
- 运算之间存在关联，后面有些运算要用到前面运算的结果；
- 流水线的工作过程有建立与排空部分。

例3.2 有一条动态多功能流水线由5段组成，加法用1,3,4,5段，乘法用\(1,2,5\)，第\(4\)段的时间为\(2 \Delta t\)，其余各段的时间均为\(\Delta t\)，而且流水线的输出可以直接返回输入端或暂存于相应的流水寄存器中。若在该流水线上计算\(\sum\limits_{i = 1}^{4}(A_i \times B_i)\)。试计算其吞吐率、加速比和效率。

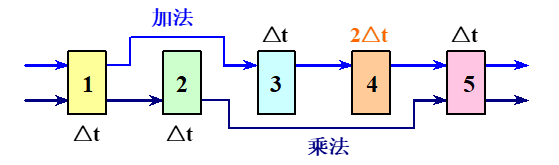
解

选择适合于流水线工作的算法
- 应先计算\(A_1 \times B_1\)、\(A_2 \times B_2\)、\(A_3 \times B_3\)和\(A_4 \times B_4\)
- 再计算\((A_1 \times B_1) + (A_2 \times B_2)\)和\((A_3 \times B_3) + (A_4 \times B_4)\)
- 再计算总的累加结果
画出时空图
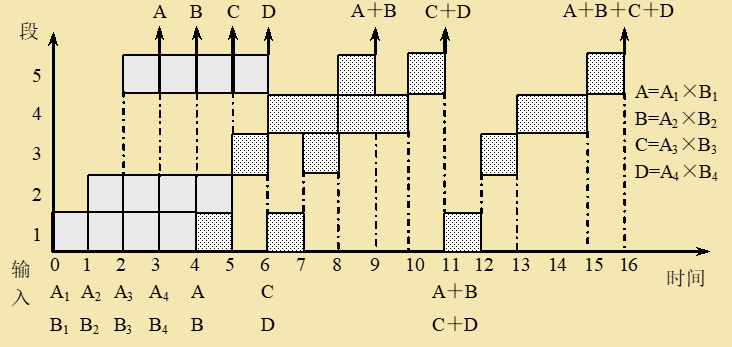
计算性能
- 吞吐率：
  
  \[TP = \frac{7}{16\Delta t} \]
- 加速比：
  
  \[S = \frac{27\Delta t}{16\Delta t} \approx 1.69 \]
- 效率：
  
  \[E = \frac{4 \times 3 + 3 \times 5}{5 \times 16} \approx 0.338 \]

流水线设计中的若干问题

瓶颈问题
- 理想情况下流水线在工作时，其中的任务是同步地每一个时钟周期往前流动一段。
- 当流水线各段不均匀时，机器的时钟周期取决于瓶颈段的延迟时间。
- 在设计流水线时，要尽可能使各段时间相等。
流水线的额外开销：流水寄存器延迟和时钟偏移开销
- 流水寄存器需要建立时间和传输延迟：建立时间：在触发写操作的时钟信号到达之前，寄存器输入必须保持稳定的时间。传输延迟：时钟信号到达后到寄存器输出可用的时间。
- 时钟偏移开销：流水线中，时钟到达各流水寄存器的最大差值时间（时钟到达各流水寄存器的时间不是完全相同的）。
- 其他问题
  - 流水线并不能减少（而且一般是增加）单条指令的执行时间，但却能提高吞吐率；
  - 增加流水线的深度（段数）可以提高流水线的性能；
  - 流水线的深度受限与流水线的额外开销；
  - 当时钟周期小到与额外开销相同时，流水已没意义。因为这时在每一个时钟周期中已没有时间来做有用的工作。
冲突问题

非线性流水线的调度

在非线性流水线中，存在反馈回路，当一个任务在流水线中流过时，可能要多次经过某些段。

流水线调度要解决的问题是：应该按照什么样的时间间隔向流水线输入新任务，才能既不发生功能段使用冲突，又能使流水线有较高的吞吐率和效率。

单功能非线性流水线的最优调度

向一条非线性流水线的输入端连续输入两个任务之间的时间间隔称为非线性流水线的启动距离。
会引起非线性流水线功能段使用冲突的启动距离称为禁用启动距离。
启动距离和禁用启动距离一般都用时钟周期数来表示，是一个正整数。
预约表：横向（向右）：时间，一般用时钟周期表示；纵向（向下）：流水线的段

例：一个5功能段非线性流水线的预约表

1 2 3 4 5 6 7 8 9

\(S_1\) √ √

\(S_2\) √ √ √

\(S_3\) √

\(S_4\) √ √

\(S_5\) √ √

如果在第\(n\)个时钟周期使用第\(k\)段，则在第\(k\)行和第\(n\)列的交叉处的格子里有一个√；

如果在第\(k\)行和第\(n\)列的交叉处的格子里面有一个√，则表示在第\(n\)个时钟周期要使用第\(k\)段。

根据预约表写出禁止表F

定义：一个由禁用启动距离构成的集合。

具体方法：对于预约表的每一行的任何一对√，用它们所在的列号相减，列出各种可能的差值，然后删除相同的，剩下的就是禁止表的元素。

在上例中：

第一行的差值有：\(8\)
第二行的差值为：\(1 , 5 , 6\)
第三行只有一个√，没有差值
第四和第五行的差值都为：\(1\)
最终的禁止表\(F = \{1 , 5 , 6 , 8\}\)。

根据禁止表F写出初始冲突向量\(C_0\)

进行从一个集合到一个二进制位串的变换。

定义：冲突向量\(C\)是一个\(n\)位的二进制位串。

设\(C_0 = (c_nc_{n - 1}...c_1)\)，则：

\[\begin{align} c_i = \begin{cases} 1 & i \in F\\ 0 & i \notin F \end{cases} \end{align} \]

\(c_0\)：表示允许间隔\(i\)个时钟周期后送入后续任务
\(c_1\)：表示不允许间隔\(i\)个时钟周期后送入后续任务

对于上述例子：

\[\begin{align} F &= \{1 , 5 , 6 , 8\}\\ C_0 &= (10110001) \end{align} \]

根据初始冲突向量\(C_0\)画出状态转换图

当第一个任务流入流水线后，初始冲突向量\(C_0\)决定了下一个任务需间隔多少个时钟周期才可以流入。

当第二个任务流入后，新的冲突向量是怎么样的呢？

假设第二个任务是与第一个任务间隔\(j\)个时钟周期流入，由于第一个任务已经在流水线中前进了\(j\)个时钟周期，其相应的禁止表中各元素的值都应该减去\(j\)，并丢弃小于等于\(0\)的值。
对冲突向量来说，就是逻辑右移\(j\)位，左边补\(0\)。
在冲突向量上，就是对他们的冲突向量进行或运算

\[SHR^{(j)} (C_0) \or C_0 \]
其中\(SHR^{(j)}\)表示逻辑右移\(j\)位。

扩展到更一般的情况：假设\(C_k\)表示当前的冲突向量，\(j\)表示允许的时间间隔，则新的冲突向量为：

\[SHR^{(j)}(C_k) \or C_0 \]

对于所有允许的时间间隔都按上述步骤求出其新的冲突变量，并且把新的冲突向量作为当前冲突向量，反复使用上述步骤，直到不再产生新的冲突向量为止。

从初始冲突向量\(C_0\)出发，反复应用上述步骤，可以求得所有的冲突向量以及产生这些向量对应的时间间隔，由此可以画出用冲突向量表示的流水线状态转移图。

有向弧：表示状态转移的方向
弧上的数字：表示引入后续任务（从而产生新的冲突向量）所用的时间间隔（时钟周期数）

对于上面的例子而言：

\(C_0 = (10110001)\)

引入后续任务可用的时间间隔为：\(2 , 3 , 4 , 7\)个时钟周期，分别采用\(2,3,4,7\)，则新的冲突向量为：

\[\begin{align} (00101100) \or (10110001) &= (10111101)\\ (00010110) \or (10110001) &= (10110111)\\ (00001011) \or (10110001) &= (10111011)\\ (00000001) \or (10110001) &= (10110001) \end{align} \]
对于新向量\((10111101)\),其可用时间间隔\(2,7\)，用类似上述的方法，可以求出其他后续的冲突向量分别为：\((10111101)\)和\((10110001)\)。
其他依次类推
在此基础上，画出状态转移示意图：

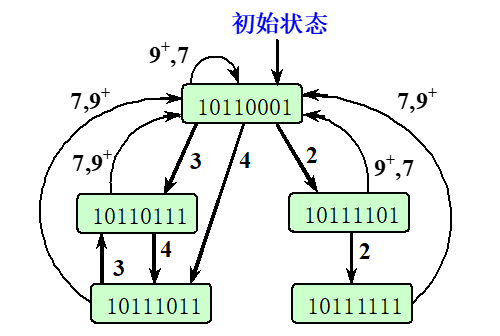
根据状态转换图写出最优调度方案

根据状态转换图，由初始状态出发，任何一个闭合回路即为一种调度方案。
列出所有可能的调度方案，计算出每种方案的平均时间间隔，从中找出其中最小者，即为最优调度方案。

在上述例子中，各种调度方案机器平均间隔时间表如下：

调度策略	平均延迟拍数
\((2 , 7)\)	\(4.5\)
\((2 , 2 , 7)\)	\(3.67\)
\((3 , 7)\)	\(5\)
\((3 , 4)\)	\(3.5\)
\((3 , 4 , 3 , 7)\)	\(4.25\)
\((3 , 4 , 7)\)	\(4.67\)
\((4 , 3 , 7)\)	\(4.67\)
\((4 , 7)\)	\(5.5\)
\((7)\)	\(7\)

最优调度方案为\((3 , 4)\)，平均间隔时间为\(3.5\)个时钟周期，吞吐率最高

方案\((3 , 4)\)是一种不等时间间隔的调度方案，与等间隔的调度方案相比，在控制上要复杂得多，为了简化控制，也可以采用等间隔时间的调度方案，但吞吐率和效率往往会下降不少。在上述例子中，等时间间隔的方案只有一个：\((7)\)，其吞吐率下降了一半。

流水线的相关与冲突

一条经典的5段流水线

一条指令的执行过程分为一下5个周期：

取指令周期（IF）：
- 以程序计数器PC中的内容作为地址，从存储器中取出指令并放入指令寄存器IR；
- 同时PC值加4（假设每条指令占4个字节），指向顺序的下一条指令。
指令译码、读寄存器周期（ID）

对指令进行译码，并用IR中的寄存器地址去访问通用寄存器组，读出所需的操作数。
执行、有效地址计算周期（EX）
- load和store指令：ALU把指令中所指定的寄存器的内容与偏移量相加，形成访存有效地址。
- 寄存器-寄存器ALU指令：ALU按照操作码指定的操作对从通用寄存器组中读出的数据进行运算。
- 寄存器-立即数ALU指令：ALU按照操作码指定的操作对从通用寄存器组中读出的操作数和指令中给出的立即数进行运算。
- 分支指令：ALU把指令中给出的偏移量与PC值相加，形成转移目标的地址。同时对在前一个周期读出的操作数进行判断，确定分支是否成功。
存储器访问、分支完成周期（MEM）：

该周期处理的指令只有load、store和分支指令。其他类型的指令在此周期不做任何操作。
- load指令：用上一个周期计算出来的有效地址从存储器重读出相应的数据；
- store指令：把指定的数据写入这个有效地址所指出的存储器单元。
- 分支指令：分支成功就把转移目标地址送入PC，分支指令执行完成。
写回周期（WB）：ALU运算值和load指令在这个周期把结果数据写入通用寄存器组。
- ALU运算指令：结果数据来自ALU
- load指令：结果数据来自存储器
在这个实现方案中：
- 分支指令需要4个时钟周期（如果把分支指令的执行提前到ID周期，则只需要2个周期）；
- store指令需要4个周期
- 其它指令需要5个周期才能完成

将上述实现方案修改为流水线实现：

一条经典的5段流水线
- 每一个周期作为一个流水段；
- 在各段之间加上锁存器（流水寄存器）

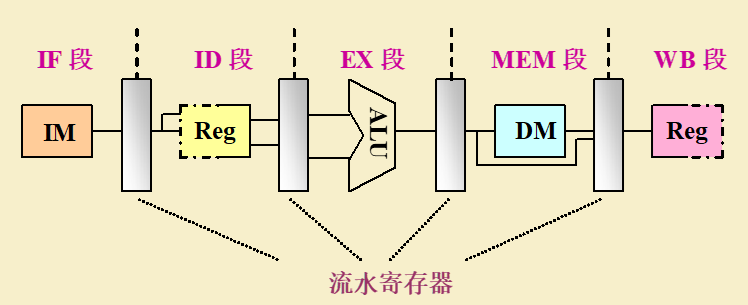
采用流水线方式实现时，应解决好以下几个问题：

要保证不会在同一时钟周期要求同一个功能段做两件不同的工作。例如：不能要求ALU同时做有效地址计算和算术运算。
避免IF段的访存（取指令）与MEM段的访存发生冲突。
- 可以采用分离的指令存储器和数据存储器。
- 一般采用分离的指令cache和数据cache。
ID段和WB段都要访问同一寄存器文件

如何解决对同一寄存器的访问冲突？

答：把写操作安排在时钟周期的前半拍完成，把读操作安排在后半拍完成。

考虑PC的问题

流水线为了能够每个时钟周期启动一条新的指令，就必须在每个时钟周期进行PC值加4操作，并保留新的PC值。这种操作必须在IF段完成，以便为取下一条指令做好准备。
但分支指令也可能改变PC的值，而且是在MEM段进行，这会导致冲突。

5段流水线的两种描述方式

第一种描述类似于时空图
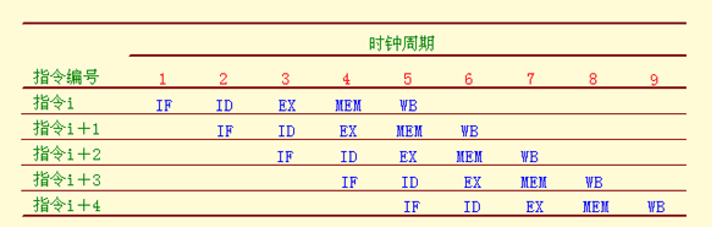
第二种描述按时间错开的数据通路序列

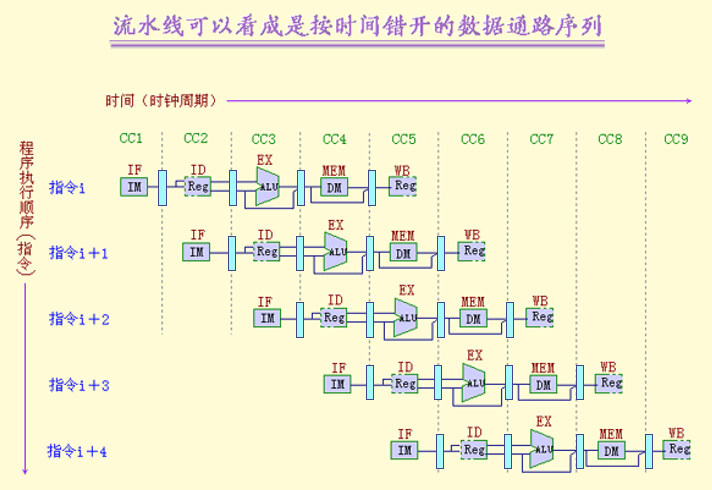
相关与流水线冲突

流水线冲突

定义：流水线冲突是指对于具体的流水线来说，由于相关的存在，使得指令流中的下一条指令不能在指定的时钟周期执行。

流水线冲突的3种类型：

结构冲突：因硬件资源满足不了指令重叠执行的要求而发生的冲突。
数据冲突：当指令在流水线中重叠执行时，因需要用到前面指令的执行结果而发生的冲突。
控制冲突：流水线遇到分支指令和其它会改变PC值的指令所引起的冲突。

带来的几个问题：

导致错误的执行结果
流水线可能会出现停顿，从而降低流水线的效率和实际的加速比。
我们约定：当一条指令被暂停时，在该暂停指令之后流出的所有指令都要被暂停，而在该暂停指令之前流出的指令则继续进行（否则就永远无法消除冲突）。

结构冲突

在流水线处理机中，为了能够使各种组合的指令都能顺利地重叠执行，需要对功能部件进行流水或重复设置资源。
如果某种指令组合因为资源冲突而不能正常执行，则称该处理机有结构冲突。
常见的导致结构冲突的原因：
- 功能部件不是完全流水
- 资源份数不够
结构冲突举例：访存冲突

有些流水线处理机只有一个存储器，将数据和指令放在一起，访存指令会导致访存冲突。
- 解决方法一：插入暂停周期（流水线气泡）
- 解决方法二：设置相互独立的指令存储器和数据存储器或设置相互独立的指令cache和数据cache
有时流水线设计者允许结构冲突的存在

主要原因：减少硬件成本，如果把流水线中的所有功能单元完全流水化，或者重复设置足够份数，那么所花费的成本将相当高。

数据冲突

当相关的指令靠得足够近时，它们在流水线中的重叠执行或者重新排序会改变指令读/写操作数的顺序，使之不同于它们串行执行时的顺序，则发生了数据冲突。

根据指令读访问和写访问的顺序，可以将数据冲突分为3种类型。

考虑两条指令i和j，且i在j之前进入流水线，可能发生的数据冲突有：
- 写后读冲突(RAW)：在i写入之前，j先去读。j读出的内容是错误的。这是最常见的一种数据冲突，它对应于真数据相关。
- 写后写冲突（WAW）：在i写入之前，j先写。最后写入的结果是i的。这种冲突对应于输出相关。
  
  写后写冲突仅发生在这样的流水线中：
  - 流水线中不只一个段可以进行写操作；
  - 指令被重新排序了。
  前面介绍的5段流水线不会发生写后写冲突，因为只在WB段写寄存器。
- 读后写冲突（WAR）：在i读之前，j先写。i读出的内容是错误的！由反相关引起。
  
  这种冲突仅发生在这样的情况下：
  - 有些指令的写结果操作提前了，而且有些指令的读操作滞后了；
  - 指令被重新排序了。
通过定向技术减少数据冲突引起的停顿

定向技术也称旁路或短路
- 关键思路：在计算结果尚未出来之前，后面等待使用该结果的指令并不真正立即需要该计算结果，如果能够将该计算结果从其产生的地方直接送到其它指令需要它的地方，那么就可以避免停顿。
- 定向的实现：EX段和MEM段之间的流水寄存器中保存的ALU运算结果总是回送到ALU的入口。当定向硬件检测到前一个ALU运算结构写入的寄存器就是当前ALU操作的源寄存器时，那么控制逻辑就选择定向的数据作为ALU的输入，而不采用从通用寄存器组读出来的数据。
- 结果数据不仅可以从某一功能部件的输出定向到其自身的输入，而且还可以定向到其它功能部件的输入。
需要停顿的数据冲突
- 并不是所有的数据冲突都可以用重定向技术来解决
- 增加流水线互锁机制，插入暂停；作用：检测发现数据冲突，并使流水线停顿，直至冲突消失。
依靠编译器解决数据冲突

让编译器重新组织指令顺序来消除冲突，这种技术称为指令调度或流水线调度。

控制冲突

执行分支指令的结果有两种：
- 分支成功：PC值改变为分支转移的目标地址。在条件判定和转移地址计算都完成后，才改变PC值。
- 不成功或失败：PC的值保持正常递增，指向顺序的下一条指令。
处理分支指令最简单的方法：冻结或者排空流水线。
- 优点：简单，前述5段流水线中，改变PC值是在MEM段进行的。给流水线带来了3个时钟周期的延迟。
把由分支指令引起的延迟称为分支延迟。
分支指令在目标代码中出现的频度：每\(3\sim 4\)条指令就有一条是分支指令。假设分支指令出现的频度是30%，流水线理想CPI = 1，则流水线的实际CPI = 1.9。
可以采取两种措施来减少分支延迟
- 在流水线中尽早判断出分支转移是否成功
- 尽早计算出分支目标地址。

3种通过软件来减少分支延迟的方法

共同点
- 对分支的处理方法在程序的执行过程中始终是不变的，是静态的。
- 要么总是预测分支成功，要么总是预测分支失败。
预测分支失败
- 允许分支指令后的指令继续在流水线中流动，就好像什么都没发送一样；
- 若确定分支失败，将分支指令看作是一条普通指令，流水线正常流动。
- 若确定分支成功，流水线就把在分支指令之后取出的所有指令转化成空操作，并按分支目地重新取指令执行。
要保证：分支结果出来之前不能改变处理机的状态，以便一旦猜错时，处理机能够回退到原先的状态。
预测分支成功

假设分支转移成功，并从分支目标地址处取指令执行。起作用的前提：先知道分支目标地址，后知道分支是否成功。前述5段流水线中，这种方法没有任何好处。

延迟分支

主要思想：从逻辑上延长分支指令的执行时间，把延迟分支看成是由原来的分支指令和若干个延迟槽构成，不管分支是否成功，都要按照顺序执行延迟槽中的指令。

分支延迟指令的调度：在延迟槽中放入有用的指令。由编译器完成。能否带来好处取决于编译器能否把有用的指令调度到延迟槽中。

三种调度方法：

从前调度
从目标处调度
从失败出调度

三种方法的要求和效果

调度策略	对调度的要求	什么情况下起作用
从前调度	被调度的指令必须与分支无关	任何情况
从目标处调度	必须保证再分支失败时执行被调度的指令不会导致错误。有可能需要复制指令。	分支成功时（但由于复制指令，有可能会增大程序空间）
从失败处调度	必须保证在分支成功时执行被调度的指令不会导致错误	分支失败时

分支延迟受到两个方面的限制：

可以被放入延迟槽中的指令要满足一定的条件；
编译器预测分支转移方向的能力。

进一步改进：分支取消机制

当分支的实际执行方向和事先所预测的一样时，执行分支延迟槽中的指令，否则就将分支延迟槽中的指令转化成一个空操作。

流水线的实现

MIPS的一种简单实现

实现MIPS指令子集的一种简单数据通路。

该数据通路的操作分为5个时钟周期
- 取指令
- 指令译码、读寄存器
- 执行、有效地址计算
- 存储器访问、分支完成
- 写回
只讨论整数指令的实现
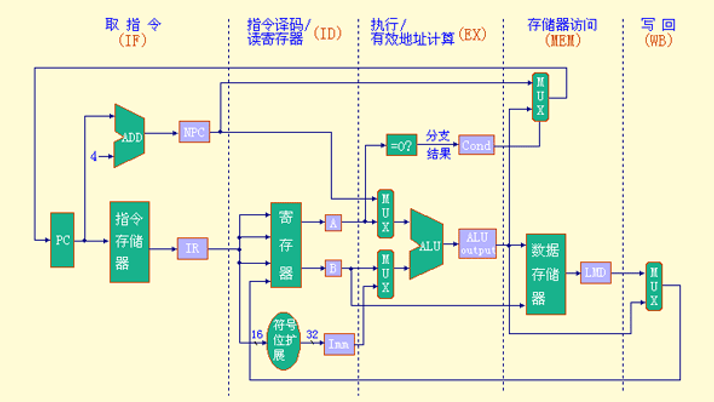
设置了一些临时寄存器。其作用如下：
- PC：程序计数器，存放当前指令的地址。
- NPC：下一条程序计数器，存放下一条指令的地址。
- IR：指令寄存器，存放当前正在处理的指令。
- A：第一操作数寄存器，存放从通用寄存器组读出来的操作数。
- B：第二操作数寄存器，存放从通用寄存器组读出来的另一个操作数。
- Imm：存放符号扩展后的立即数操作数。
- Cond：存放符号扩展后的立即数操作数。
- ALUo：存放ALU的运算结果。
- LMD：存放load指令从存储器读出的数据。

一条MIPS指令最多需要以下5个时钟周期：

取指周期（IF）
指令译码、读寄存器周期（ID）
执行、有效地址计算周期（EX）
存储器访问、分支完成周期(MEM)
写回周期（WB）

基本的MIPS流水线

每一个时钟周期完成的工作看作是流水线的一段，每个时钟周期启动一条新的指令。

流水实现的数据通路
- 设置了流水寄存器
  - 段与段之间设置流水寄存器
  - 流水寄存器的名称用其相邻的两个段的名称拼合而成，如ID/EX表示ID段和EX段之间的流水寄存器。
  - 每个流水寄存器是由若干个寄存器构成的
  - 寄存器的命名形式为：x , y
  - 所包含的字段的命名形式为：x , y[s]，其中x表示流水寄存器的名称，y表示具体寄存器名称，s是字段名。例如：ID/EX IR：流水寄存器ID/EX中的子寄存器IR；ID/EX IR[op]表示该寄存器的op字段。
  - 流水寄存器的作用：将各段的工作隔开，使得它们不会相互干扰；保存相应段的处理结果。
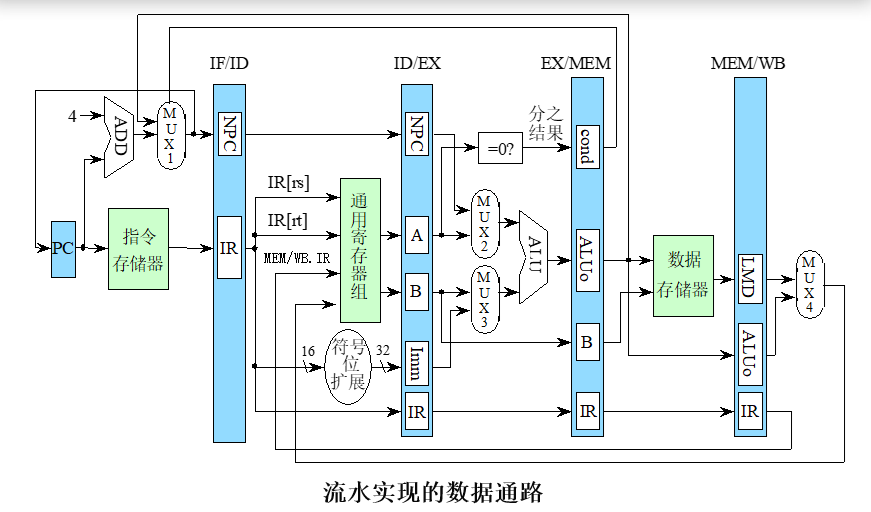
- 增加了向后传递IR和从MEM/WB.IR回送到通用寄存器组的连接。
- 将对PC的修改移到了IF段，以使PC能及时地加4，为取下一条指令做好准备。

posted @ 2022-04-17 21:43 cherish-lgb 阅读(1076) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

風月无关我