最大流问题
问题引入:在物流网络中,从一个城市(称为源结点)发送一批货物到另一个城市(称为汇点)。假设源结点可以源源不断地提供货物,汇点可以来者不拒地接收货物;路径连接在任意两个城市之间,但路径上有运输容量有限制。货物从源结点到汇点可以选择不同的运输路径。问:在不违反任何路径容量限制的条件下,从源结点到汇点运送货物的最大速率是多少——这一问题的抽象称为最大流问题。
用带权有向图来表示:
- 结点表示城市
- 结点间的有向边表示运输路径和物流的方向
- 边上的权重表示运量限制
这样用来表示“流”的图称为“流网络”。
一些约定:
- 流量守恒:除源结点和汇点外,其它结点上物料只是“流过”, 即物料进入的速率等于离开的速率,不积累和聚集;
- 物料的生成速率和接收速率恒定且足够快、足够多,满足需要;
- 每条边上的容量是物料通过该边的最大速率,不能突破。
流网络
流网络是一个有向图\(G=(V , E)\),边上定义有容量函数\(c:E \to R^+ \cup \{0\}\)
- 有一个源点\(s\)和汇点\(t\)
- 有向边表示流向
- 每条边\((u , v) \in E\)上有一个非负的容量值:\(c(u , v) \geq 0\);如果\((u , v) \notin E\),为方便起见,定义\(c(u , v) =0\)
- 如果边集合\(E\)中包含\((u ,v)\),则图中不包含其反向边\((v , u)\)
- 图中不允许有自环
- 流网络是连通图,每个结点都在从\(s\)到\(t\)的某条路径上
- 除源结点外,每个结点至少有一条流入的边
- 除汇点外,每个结点至少有一条流出的边
- \(|E| \geq |V| - 1\)
流是定义在\(G\)上的一个实值函数,记为:\(f : V \times V \to R\),并满足以下两条性质:
-
容量限制:对于所有的结点\(u , v \in V\),有:
\[0 \leq f(u , v) \leq c(u , v) \] -
流量守恒:对于所有的结点\(u \in V - \{s , t\}\),有:
\[\sum\limits_{v \in V} f(v , u) = \sum\limits_{u \in V} f(u , v) \]这里\(f(u , v)\)表示从结点\(u\)到结点\(v\)的流。若\((u , v) \notin E\) , 记\(f(u , v) = 0\),表示从结点\(u\)到结点\(v\)没有流。
流的值:一个流\(f\)的值定义为流出源结点\(s\)的总流量减去流入源结点\(s\)的总流量,用\(|f|\)表示:
但通常流网络中没有流入源结点的边,因此\(\sum\limits_{v \in V} f(v , s) = 0\)。
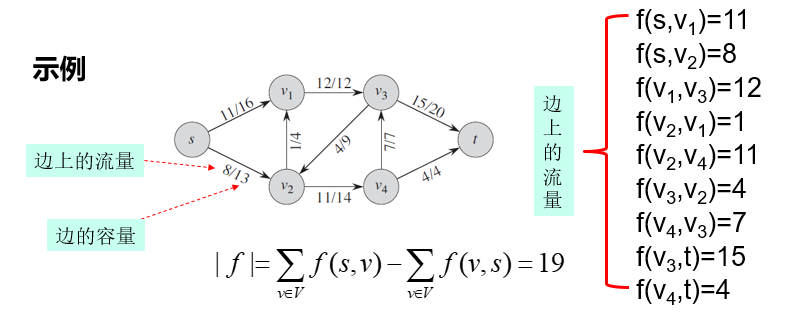
最大流问题:在给定的流网络\(G\)找一个流值最大的流的问题
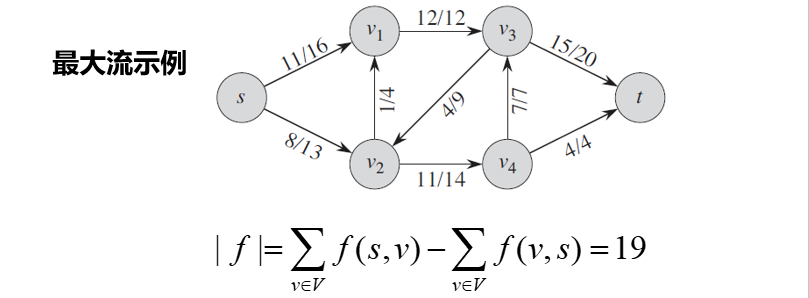
上述定义的流网络有两个标准特性:
- 无反向边,或者称为反平行边,即如果\((u , v) \in E\),则\((v , u) \notin E\)。这里的\((u , v) , (v , u)\)互为反平行边。
- 只有单一的源结点和汇点
不满足上述要求的流网络称为非标准的一般流网络,对于一般流网络,需要转化成标准流网络进行处理。
-
具有反平行边的流网络的转化方法
对每一组反平行边\((u ,v)\)和\((v , u)\),选择其中的一条,比如 \((u , v)\)然后加入一个新的结点\(v'\),将其分为两条边\((u , v')\)和\((v' , v)\),并将两条新加入的边的容量设为被替代掉的边\((u , v)\)的容量,即\(c(u , v') = c(v' , v) = c(u , v)\)
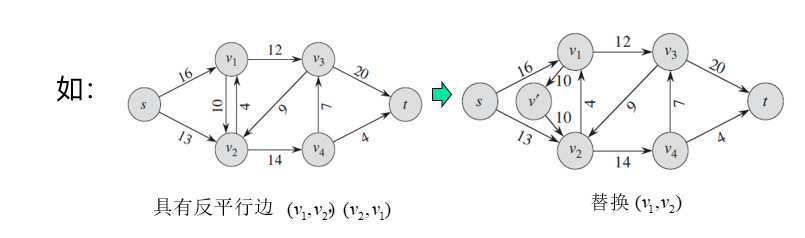
-
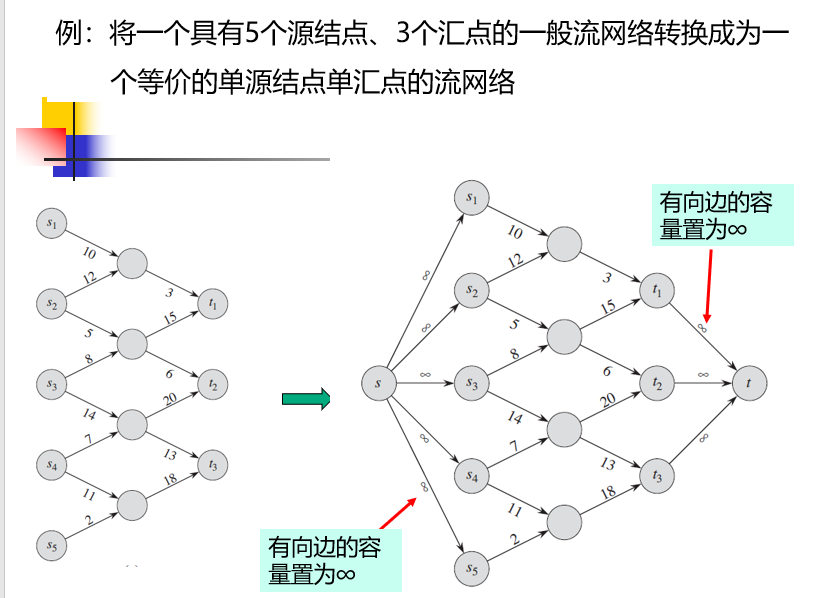
具有多个源结点和多个汇点的网络的转化方法
- 如果流网络中有多个源结点\(\{s_1 , s_2 , ... , s_m\}\),则加入一个超级源结点\(s\),并加入有向边\((s , s_i) \;\forall 1\leq i \leq m\),然后令\(c(s , s_i) = \infin\;\forall\;1\leq i \leq m\)
- 如果有多个汇点\(\{t_1 , t_2 ,..., t_n\}\),则加入一个超级汇点,并加入有向边\((t , t_i) ,c(t , t_i) = \infin \;\forall 1 \leq i \leq n\)
超级源结点\(s\)能够给原来的多个源结点\(s_i\)提供所需的流量,超级汇点\(t\)可以消费原来所有汇点\(t_i\)所消费的流量。可以证明转化后的两个网络是等价的,具有相同的流。
求流网络的最大流的基本思想:从最小流值开始,一点一点地增加,直到最大值
Ford-Fulkerson方法
基本思想:通过不断增加可行流值的方式找到最大流:从流值为\(0\)的初始流开始,通过某种方法,对流值进行增加;确认无法再增加流值时,即得到最大流。
要点:1.对流网络\(G\),在其“残存网络\(G_{f}\)”中寻找一条增广路径\(p\);2.如果存在增广路径,则对路径上边的流量进行修改,以增加流网络的流量;3.重复上述过程直到不再存在增广路径为止。
判断是否得到最大流的理论基础是最大流最小切割定理,该定理将说明在算法终止时将获得一个最大流。

残存网络
对给定流网络\(G\)和流量\(f\),\(G\)的残存网络\(G_f\)由\(G\)中的结点和以下的边组成:
对于\(G\)中任意边\((u , v)\):
-
若\(f(u , v) < c(u , v)\),则将边\((u , v)\)和它的反向边\((v , u)\)都加入\(G_f\),并设其残存容量为:
\[c_f(u , v) = c(u , v) - f(u , v)\\ c_f(v , u) = f(u , v) \]残存容量\(c_f(u , v)\)反映了边上可以增加流量的空间。
-
如果边\((u , v)\)的流量等于其容量,则\(c_f(u , v) = 0\),此时\((u ,v)\)不加入\(G_f\),即只有有多余流量的边才加入\(G_f\)。但仍将反向边\((v , u)\)加入\(G_f\),并置\(c_f(v , u) = f(u , v)\)。目的是对一个正向流量\(f(u , v)\)进行缩减,且最多减少\(f(u , v)\)
残存容量
设流网络\(G = (V , E)\),\(f\)是\(G\)中的一个流,\(u , v \in V\),定义边\((u , v)\)的残存容量\(c_f(u , v)\)为:
残存网络由\(f\)所诱导的图\(G\)的残存网络记为\(G_f = (V , E_f)\),其中\(E_f = \{(u , v) \in V \times V : c_f(u , v) > 0\}\)。即\(G_f\)由残存流量大于\(0\)的边构成,且\(|E_f| \leq 2|E|\)
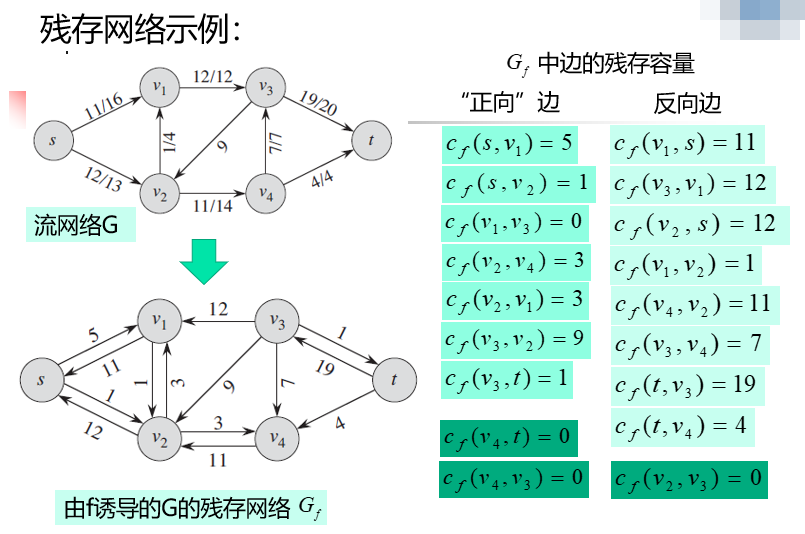
残存网络\(G_f\)类似于一个容量为\(c_f\)的流网络,但\(G_f\)不满足流网络的定义:因为\(G_f\)可能包含边\((u,v)\)和它的反向边\((v,u)\)。但除此之外,残存网络和流网络具有同样的性质。因此也可以在残存网络中定义一个流:
设\(f\)是\(G\)的一个流,\(f'\)是残存网络\(G_f\)中的一个流,则:
- \(f'\)针对残存网络\(G_f\)中的容量\(c_f\)定义且满足流的性质-容量限制、流量守恒
- \(f'\)指出如何在原来的流网络中增加流
定义\(f\uparrow f'\)为流\(f'\)对流\(f\)的递增,是一个从\(V \times V\)到\(R\)的函数:
其中\(f'(u , v)\)表示边\((u ,v)\)上流量的增加;\(f'(v , u)\)表示边\((u , v)\)上流量的减少。
在残存网络中将流量发送到反向边上等同于在原来的网络中缩减流量。在残存网络中将流量推送回去称为抵消操作(cancellation),其意义在于调整流网络中总流量的分布。
\(f\uparrow f'\)是最终成为原网络中的一个流,是基于\(f'\)对原网络中流\(f\)调整的结果。
引理26.1:设\(G=(V,E)\)为一个流网络,源结点为\(s\),汇点为\(t\)。设\(f\)为\(G\)中的一个流。设\(G_f\)为由流\(f\)所诱导的\(G\)的残存网络,设\(f'\)为\(G_f\)中的一个流。那么\(f\uparrow f'\)是\(G\)的一个流,其值为 :
\[|f\uparrow f'| = |f| + |f'| \]
引理26.1说明:如果在\(G'\)中能够找到一个合法的流\(f'\) ,则可以用\(f'\) 对\(G\)上原来的流\(f\)进行调整,调整的结果是:
如果\(|f'| > 0\),则可以达到对\(f\)递增的效果。
上述引理证明思路:首先,证明\(f\uparrow f'\)是图\(G\)的一个流,即\(f\uparrow f'\)对\(E\)中的每条边满足容量限制,且对每个结点\(V - \{s , t\}\)满足流量守恒性质。其次,证明流量值公式成立。
证明如下:
首先证明\(f\uparrow f'\)是图\(G\)的一个流且满足容量限制和流量限制。
-
容量限制
根据定义,如果边\((u ,v) \in E\),则\(c_f(v , u) = f(u , v)\),而且\(f'(v , u) \leq c_f(v , u) = f(u , v)\)
故有:
\[(f\uparrow f')(u , v) = f(u , v) + f'(u , v) - f'(v , u)\\ \geq f(u , v) +f'(u , v) - f(u ,v)\\ = f'(u ,v)\\ \geq 0 \]即\(f\uparrow f'\)是非负的。
此外:
\[(f\uparrow f')(u , v)=f(u ,v) + f'(u , v) - f'(v , u)\\ \leq f(u , v) + f'(u , v)\\ \leq f(u , v) + c_f(u , v)\\ =f(u , v) + c(u , v) - f(u , v)\\ = c(u , v) \]即递增后,流\(f\uparrow f'\)也不超过容量的限制。
容量限制:对任一结点对\(u\)和\(v\),满足\(0 \leq f(u , v) \leq c(u , v)\)
-
流量守恒
因为\(f\)和\(f'\)均遵守流量守恒性质,所以对所有的\(u \in V - \{s , t\}\)结点,有:
\[\sum\limits_{v \in V} (f\uparrow f')(u , v) = \sum\limits_{v \in V} (f(u , v) + f'(u , v) - f'(v , u))\\ = \sum\limits_{v \in V} f(v , u) + \sum\limits_{v \in V} f'(v , u) - \sum\limits_{v \in V} f'(u , v)\\ = \sum\limits_{v \in V} (f(v , u) + f'(v , u) - f'(u , v))\\ = \sum\limits_{v \in V} (f\uparrow f')(v , u) \]流量守恒:对于\(u \in V - \{s ,t\}\),有\(\sum\limits_{v \in V}f(v , u) = \sum\limits_{v \in V} f(u , v)\)
再证明\(|f\uparrow f'| = |f| + |f'|\):
定义:\(V_1 = \{v : (s , v) \in E\}\) \(V_1\)是所有从源结点有边可到达的结点的集合
\(V_2 = \{v : (v , s) \in E\}\) \(V_2\)是所有有边通往源结点\(s\)的结点的集合
由于\((s,v)\)和\((v , s)\)不可能同时存在与流网络中所以有:
则有
注:若\((w , x) \notin E\),则\(|f\uparrow f'(w , x)| = 0\)
根据\(f\uparrow f'\)的定义,重组上式有:
得证
增广路径
对给定流网络\(G=(V , E)\)和流\(f\),增广路径\(p\)是其残存网络\(G_f\)中一条从源结点\(s\)到汇点\(t\)的简单路径。根据残存网络的定义,对于增广路径上的一条边\((u,v)\),其可增加的流值最大为该边的残存容量\(c_f(u , v)\)。对于一条增广路\(p\),能增加的最大流值称为该路径的残存容量,等于\(p\)上所有边残存容量的最小值,即:
残存容量最小的边是瓶颈,增广路径的流量受其限制。
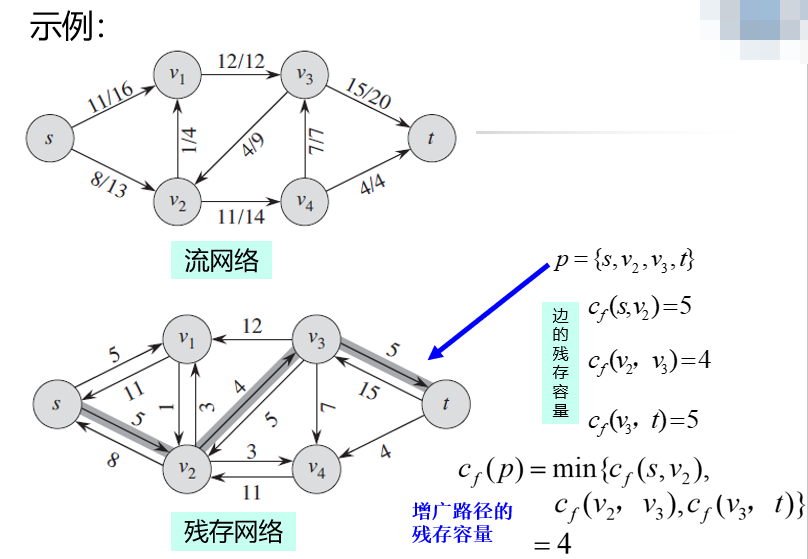
引理26.2:设\(G = (V , E)\)为一个流网络,\(f\)是图\(G\)的一个流。记\(p\)为其残存网络\(G_f\)中的一条增广路径。定义一个函数\(f_p : V \times V \to R\)如下:
则\(f_p\)是残存网络\(G_f\)中的一个流,其值为\(|f_p| = c_f(p) > 0\)。
该引理告诉我们,\(G\)的残存网络\(G'\)中,一个合法的流\(f'\)怎么去找:\(f_p\)就是这样的一个合法的流。所以可以用\(f_p\)为\(f\)进行递增计算。
证明略。
\(f_p\)的作用:将流\(f\)增加\(f_p\)的量,得到的仍是\(G\)的一个流,且该流的值更加接近最大值。
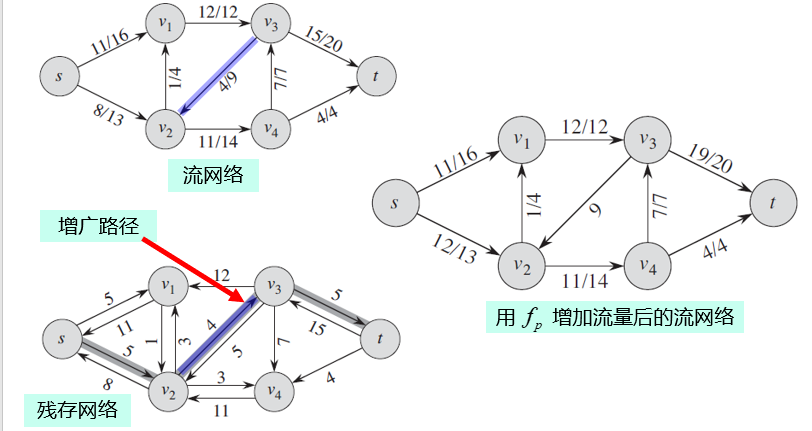
推论26.3:设\(G = (V , E)\)为一个流网络,\(f\)是图\(G\)的一个流。记\(p\)为其残存网络\(G_f\)中的一条增广路径。设\(f_p\)是上式定义的残存网络的流,假定将\(f\)增加\(f_p\)的量,则函数\(f\uparrow f_p\)是图\(G\)的一个流,其值为\(|f \uparrow f_p| = |f| + |f_p| > |f|\)
证明略。
利用残存网络和增广路径实现Ford-Fulkerson方法示例:
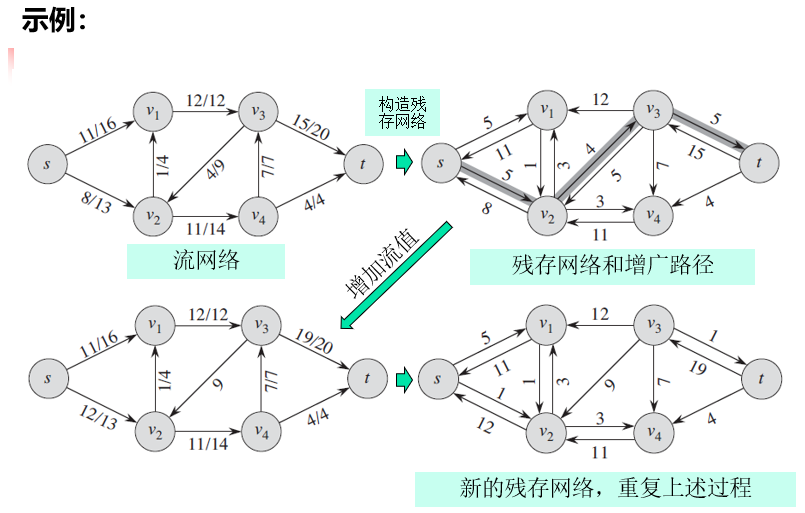
残存网络和增广路径总结:
- 已经解决的问题:如何增加流值-利用增广路径
- 未解决的问题:如何判断算法终止时,确实找到了最大流呢?-利用最大流最小切割定理进行判定
最大流最小切割定理
建立最大流和切割容量之间的关系,从而建立最大流和残存网络增广路径上的残存容量之间的关系。一个流是最大流当且仅当其残存网络中不包含任何增广路径。
流网络的切割
给定流网络\(G=(V , E)\),源结点为\(s\),汇点为\(t\)。定义一个切割\((S , T)\),将结点集合\(V\)分为两部分\(S\)和\(T = V - S\),使得\(s \in S , t \in T\)。若\(f\)是\(G\)上的一个流,定义横跨切割\((S , T)\)的净流量\(f(S , T)\)为:
定义切割\((S , T)\)的容量为:\(c(S , T) = \sum\limits_{u \in S}\sum\limits_{v \in T}c(u , v)\)
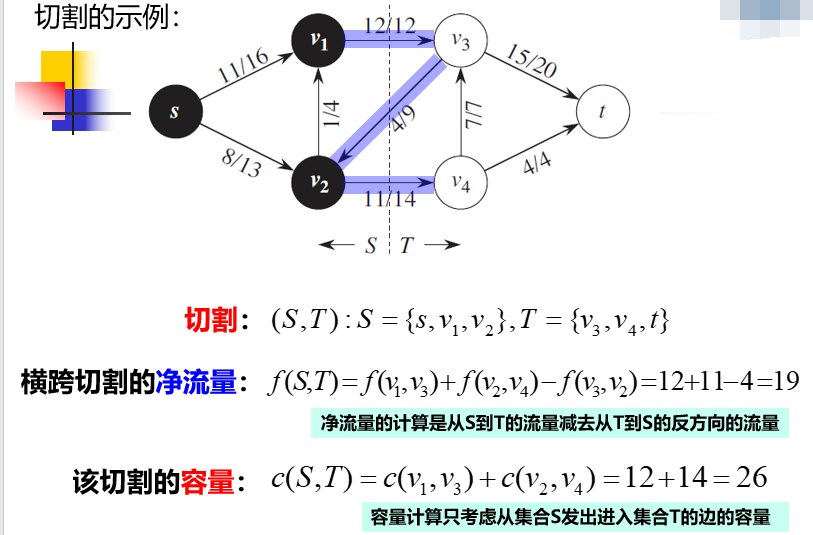
最小切割:一个网络的最小切割是网络中容量最小的切割。
流、切割净流量和切割容量之间的关系
引理26.4:设\(f\)为流网络\(G\)的一个流,该流网络的源结点为\(s\),汇点为\(t\),设\((S , T)\)为流网络\(G\)的任意切割,则横跨切割\((S , T)\)的净流量为\(f(S , T) = |f|\)。
上述引理说明对流网络的任意切割\((S , T)\),切割截面上的净流量就等于流网络的流量。而且横跨切割净流量都相同,都等于流的值\(|f|\)。
证明略。
推论26.5:流网络\(G\)中任意流\(f\)的值不能超过\(G\)的任意切割的容量。
证明:谁\((S , T)\)为流网络\(G\)的任意切割,设\(f\)为\(G\)中的任意流。根据引理26.4和容量限制,可以得到:
容量限制:\(0 \leq f(u , v) \leq c(u , v)\)
上述推论说明任何流包括最大流都不能超过最小切割的容量的限制。
最大流最小切割定理:设\(f\)为流网络\(G = (V , E)\)中的一个流,该流网络的源结点为\(s\),汇点为\(t\),则下面的条件等价:
- \(f\)是\(G\)的一个最大流
- 残存网络\(G_f\)不包括任何增广路径
- \(|f| = c(S , T)\),其中\((S , T)\)是流网络\(G\)的某个切割
最大流最小切割定理说明流网络\(G\)的最大流\(f\)在流的值等于任意切割的容量时到达,而此时在对应的残存网络\(G_f\)中不再有增广路径。所以可以用有无增广路径判断当前流\(f\)是否是最大流,如果是,则算法也可以终止了。
无增广路径的含义:对当前流\(f\),由\(f\)诱导的残存网络\(G_f\)中不再有从\(s\)到\(t\)的、路径残余容量大于\(0\)的简单路径\(p\)。即不再有路径\(p\)使得\(|f_p| = c_f(p) > 0\)。而\(G_f\)中没有残余容量等于\(0\)的边。所以无增广路径事实上与\(G_f\)中没有从\(s\)到\(t\)的路径等价。
证明略
Ford-Fulkerson算法的细化:

寻找增广路径的方法——深度优先搜索或者广度优先搜索
Ford-Fulkerson算法的运行示例
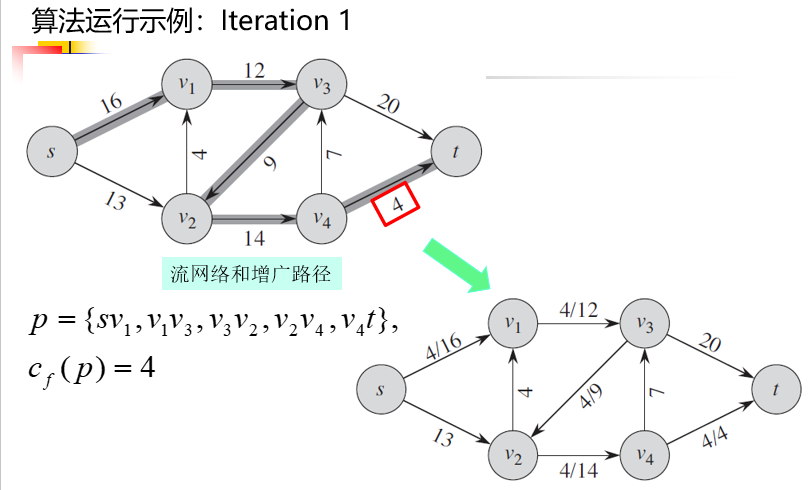
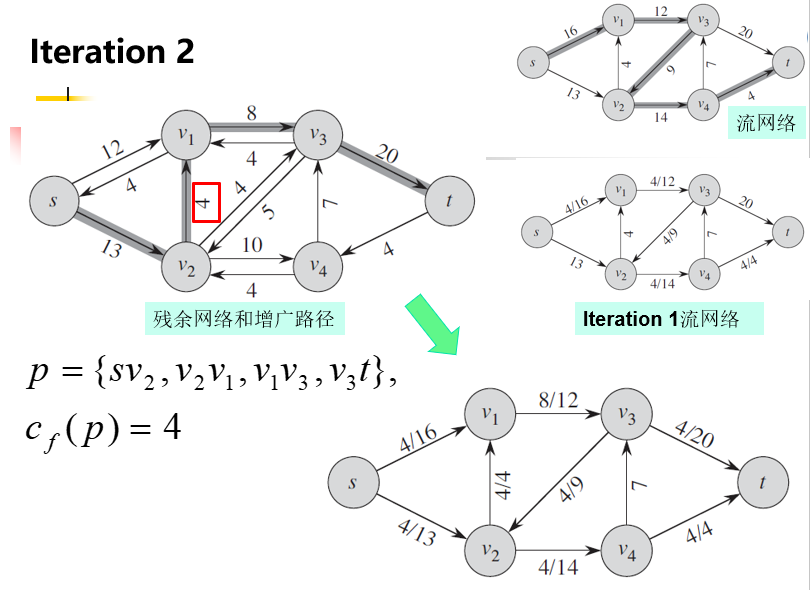
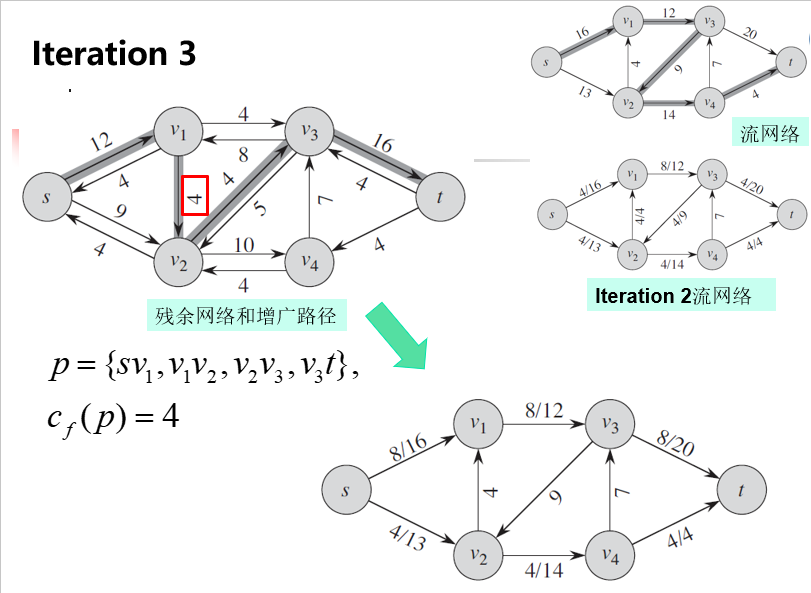
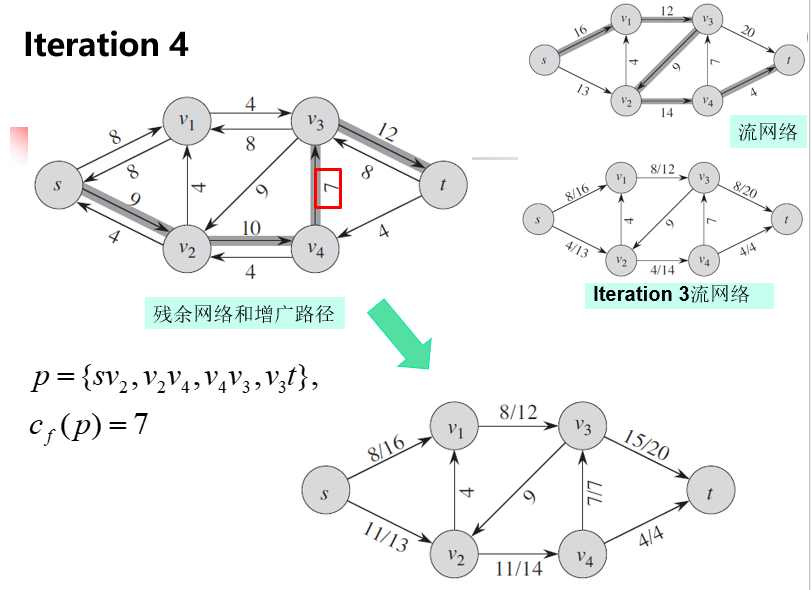
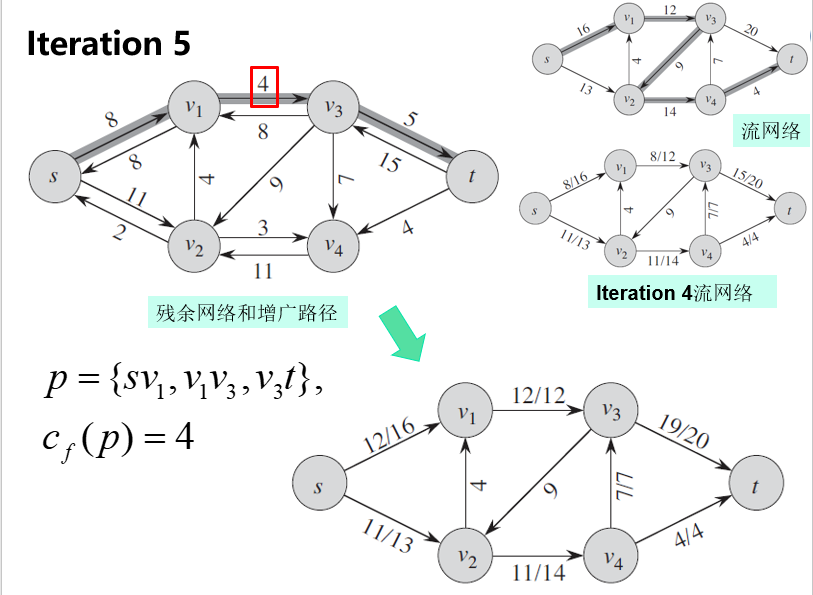
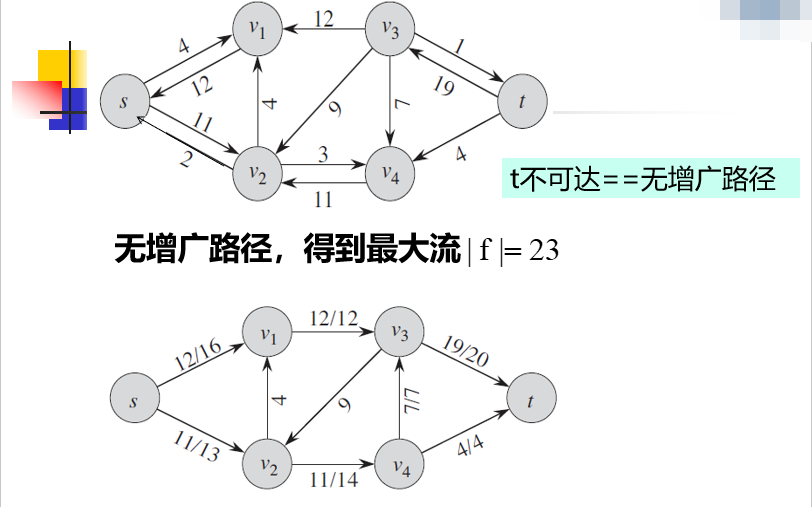
Ford-Fulkerson算法复杂度分析
假定:所有的容量均为整数。
时间复杂度:\(O(|E| \times |f^{*}|)\),其中\(E\)是流网络的边集,\(f^{*}\)是最大流值。注:如边的容量是无理数时,Ford-Fulkerson算法可能不能终止,也就是不会得到最大流。
运行时间分析:
\(while\)循环的次数:因为每一次循环,流值至少增加\(1\),所以最多有\(O(|f^{*}|)\)循环。每次循环做三个主要操作:计算残存网络、寻找增广路径和更新每条边的流值。
- 计算残存网络需要计算每条边的残存容量,运行时间为\(O(|E|)\)
- 利用深度优先搜索或者广度优先搜索,计算增广路径,运行时间为\(O(|V| + |E|) \in O(|E|)\)
- 更新每条边的流值的时间是:\(O(|E|)\)
故总的计算时间为:\(O(|E| \times |f^{*}|)\)
算法存在的问题:时间复杂性与最大流值有关,当最大流值非常大时,效率较低。
Edmonds-Karp算法
Edmonds-Karp算法仍然是基于Ford-Fulkerson方法,不同的是使用广度优先搜索寻找源结点到汇点的最短路径作为增广路径,从而得到不依赖于最大流值的运行时间上界

Edmonds-Karp算法使用广度优先搜索寻找最短路径作为增广路径,时间复杂度:\(O(VE^2)\)
Edmonds-Karp算法运行时间分析:
- 在残存网络中,采用广度优先搜索找一条从\(s\)到\(t\)的最短路径的时间是\(O(E)\)。
- 可以证明,随着算法的进行,流的值不断增加,同时增广路径的长度也逐步是递增的。这使得在算法的整个执行过程中,总共最多会处理\(O(VE)\)条关键边。
故Edmonds-Karp算法运行时间为:\(O(VE^2)\)
证明过程:
令\(\delta_f(u , v)\)表示残存网络中\(G_f\)中从结点\(u\)到结点\(v\)的最短路径距离,这里每条边的权重为单位距离,路径长度等于路径上的边数。
引理4:如果Edmonds-Karp算法运行的流网络\(G = (V , E)\)上,该网络的源结点是\(s\)汇点为\(t\),则对于所有结点\(v \in V - \{s , t\}\),残存网络\(G_f\)中的最短路径距离\(\delta_f(s , v)\) 随着每次流量的递增而单调递增
证明:利用反证法证明。
假设对于某个结点\(v \in V - \{s , t\}\),存在一个流量递增操作,导致从源结点\(s\)到\(v\)的路径距离减小。
设\(f\)是第一个导致某条最短路径距离减少的流量递增操作之前的流量,\(f'\)是递增操作之后的流量。 设\(v\)是在流递增操作中最短路径被减小的结点中\(\delta_f(s , v)\)最小的结点,根据假设,应有\(\delta_{f'}(s , v) < \delta_f(s , v)\)。设\(p = s...\to u \to v\)为残存网络\(G_{f’}\)中从源结点\(s\)到结点\(v\)的一条最短路径。可以得到\((u , v) \in E_{f'}\),并且\(\delta_{f'}(s , u) = \delta_{f'}(s , v) - 1\) 。根据\(v\)的选取,可以得到:\(\delta_{f'}(s , u) \geq \delta_f(s , u)\)。我们断言\((u , v) \notin E_f\),否则有:
这与假设\(\delta_{f'}(s , v) < \delta_f(s , v)\)矛盾。\(v\)是最短路径变小的结点中最短路径最小的结点,所以\(s\)到\(u\)的最短路径不能变小,否则应选\(u\)而不是\(v\)了。
由上可得:\((u , v) \in E_{f'}\)时有\((u , v) \notin E_{f}\)。
- \((u , v) \notin E_{f}\):以为着相对流\(f,f(u , v) = c(u , v) , c_f(u , v) = 0\),所以\((u , v)\)不在残存网络\(G_f\)中
- \((u , v) \in E_{f'}\):意味着相对流\(f',f'(u , v) < c(u , v) , c_{f'}(u , v) > 0\)。也因此有由残存网络\(G_f\)中计算得到的增广路径上边\((v,u)\)上有流量,导致增量计算以后,边\((u , v)\)上的流量因边\((v , u)\)上流量的抵消而减少,从而有\(c_{f'}(u , v) = c(u , v) - f'(u , v) > 0\)。
这也意味着\((v , u)\)是相对于流\(f\)的残存网络\(G_f\)的增广路径上的一条边,而Edmonds-Karp算法中,增广路径是最短路径,所以这也意味着,\((v , u)\)存在于残存网络\(G_f\)中\(s\)到\(u\)的最短路径上,而且是从源结点\(s\)到结点\(u\)的最短路径上的最后一条边。因此有:
所以\(s\)到\(v\)的最短路径并没有减小,与假设\(\delta_{f'}(s ,v) < \delta_f(s , v)\)相矛盾。所以流量递增操作导致从源结点\(s\)到\(v\)的路径距离减小不成立。
定理2:如果Edmonds-Karp算法运行在源结点为\(s\)汇点为\(t\)的流网络\(G=(V,E)\)上,则算法执行的流量递增操作的次数为\(O(VE)\)
关键边:在残存网络\(G_f\)中,如果一条路径\(p\)的残存容量是该条路径上边\((u,v)\)的残存容量,即 ,那么\((u,v)\)称为增广路径p上的关键边。任何一条增广路径上至少存在一条关键边;增流后,当前增广路径上的关键边将从残存网络中消失。
由前一引理已知:Edmonds-Karp算法中,当流值增加的时候,从\(s\)到每个结点的距离会增加。下面利用这个性质证明:每条边\((u,v)\)成为关键边之后,在下一次成为关键边之时,\(s\)到\(u\)的最短距离至少会增加\(2\)。
设\((u , v) \in V\),且\((u , v) \in E\)。考虑\((u , v)\)第一次成为关键边时:\((u , v)\)处于增广路径上,而增广路径是最短路径,所以有:\(\delta_f(s ,v) = \delta_f(s , u) + 1\)。而一旦对流进行增加后,\((u , v)\)就从下一面的残存网络中消失,直到某一步时从\(u\)到\(v\)的流量减小了。此时\((v , u)\)是增广路径上的边,并且有正流量。记此时的流为\(f'\),则有:\(\delta_{f'} (s , u) = \delta_{f'}(s , v) + 1\)
根据\(\delta_f(s , v) \leq \delta_{f'}(s , v)\)有:
通过上述分析得到:当\((u , v)\)从成为关键边到再次成为关键边,从\(s\)到\(u\)的距离至少增加2个单位。
\(s\)到\(u\)的距离最初至少为\(0\),而\((u,v)\)成为增广路径上的边时,这条路径上的中间结点不可能包含\(t\)( \((u,v)\)能成为增广路径上的边,意味着\(u\neq t\),路径上的中间结点只可能是除\(u\)和\(t\)以外的其他结点)。因此,一直到\(u\)成为不可到达结点之前(最后成为不可达结点的时候意味着流网络中不再有增广路径),\(s\)到\(u\)的距离最大是\(|V|-2\)。因此,从\((u,v)\)第一次成为关键边后算起,\((u,v)\)最多还能成为关键边的次数至多是\(\frac{|V| - 2}{2} = \frac{|V|}{2} - 1\)。 即\((u,v)\)能成为关键变的总次数最多为 \(\frac{|V|}{2}\)。注意到每次流值增加,都会至少有一条关键边,因此流值递增的操作次数至多为\(O(|V||E|)\) 。
最后,由于一共有\(O(E)\)对结点可以在残存网络中有边彼此相连,每条边都有可能成为关键边。 根据上面的分析,在Edmonds-Karp算法执行的整个过程中,每条边最多有\(\frac{|V|}{2}\)次机会成为关键边,所以在算法执行的整个过程中关键边的总数为\(O(VE)\)。而每条增广路径至少有一条关键边,每条增广路径意味着要对流网络进行一次流量递增计算,所以Edmonds-Karp算法执行的流量递增操作的次数为\(O(VE)\)。
证毕。
最大流算法的应用:寻找二分图的最大匹配
建立超级源点和超级汇点,边的流量为\(1\),跑最大流算法,最终的最大流就是最大匹配数。详情可以参考 二分图最大匹配
作者:cherish.
出处:https://home.cnblogs.com/u/cherish-/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号