多源最短路
问题描述:给定一个带权重的有向图\(G = (V , E)\),其权重函数为:\(\omega : E \to R\)。在图中,对所有的结点对\(u , v \in V\) , 找出从结点\(u\)到结点\(v\)的最短路径。
该问题的解以表格(二维数组)的形式给出:第\(u\)行第\(v\)列给出从结点\(u\)到结点\(v\)的最短路径权重。一条路径的权重是组成该路径的所有边的权重之和。
一些约定:
-
结点编号:不失一般性,结点编号为\(1 , 2 , ... , |V|\)。
-
成本邻接矩阵:图\(G\)用一个\(n \times n\)的邻接矩阵\(W = (w_{i , j})\)表示,其中
\[w_{i , j} = \begin{cases} 0 & i = j\\ weight & i \neq j , (i , j) \in E\\ \infin & i \neq j , (i , j) \notin E \end{cases} \] -
允许存在权重为负值的边,但不能包含权重为负值的环路,否则无解
-
最短路径矩阵:算法的输出为一个\(n \times n\)的最短路径矩阵,\(D = (d_{i , j})\),其中\(d_{i , j}\)表示从结点\(i\)到结点\(j\)的一条最短路径的权重。算法结束时有:\(d_{i , j} = \delta(i , j)\)
-
前驱结点矩阵
前驱结点矩阵记为:\(\prod = (\pi_{i , j})\),其中
\[\pi_{i , j} = \begin{cases} NIL & i = j \;or\;不存在从i到j的路径\\ 从结点i到结点j的某条最短路径上结点j的前驱结点 \end{cases} \]利用前驱结点矩阵\(\prod\)可以计算出每对结点间的最短路径。前驱结点矩阵\(\prod\)的第\(i\)行所诱导的子图是一棵根结点为\(i\)的最短路径树。对于每个结点\(i \in V\),定义图\(G\)中对于结点\(i\)的前驱子图为\(G_{\pi , i} = (V_{\pi , i} , E_{\pi , i})\)其中
\[V_{\pi , i} = \{j \in V : \pi_{i , j} \neq NIL\} \cup \{i\}\\ E_{\pi , i} = \{(\pi_{i , j} , j) : j \in V_{\pi , i} - \{i\}\} \] -
PRINT-ALL-PAIRS-SHORTEST-PATH过程:
如果\(G_{\pi,i}\)是一棵最短路径树,则PRINT-ALL-PAIRS-SHORTEST-PATH过程输出从结点\(i\)到结点\(j\)的一条最短路径。

最短路径和矩阵乘法
该部分给出有向图所有结点对最短路径问题的一种动态规划算法。时间复杂度\(\Theta(V^4)\),然后改进到\(\Theta(V^3logV)\)。
最短路径的最优子结构性质:每条路径都是最短路径
考虑从结点\(i\)到结点\(j\)的一条最短路径\(p\)。假定\(p\)至多包含\(m\)条边(假定没有权重为负值的环路),且\(m\)为有限值。
- 如果\(i=j\),则\(p\)中不包含任何边,所以\(p\)的权重等于\(0\)。
- 如果\(i\neq j\),则将路径\(p\)分解为\(i \overset{p'}\leadsto k \to j\),其中\(p'\)至多包含\(m - 1\)条边,根据引理24.1,\(p'\)是从\(i\)到\(k\)的一条最短路径,且\(\delta(i , j) = \delta(i , k) + \omega_{k , j}\)
递归解
设\(I_{i , j}^{(m)}\)是从结点\(i\)到结点\(j\)的至多包含\(m\)条边的任意路径中的最小权重。
-
当\(m = 0\)时,表示从结点\(i\)到结点\(j\)中间没有边的最短路径,所以有
\[I_{i , j}^{(0)} = \begin{cases} 0 & if \; i = j\\ \infin & if\; i \neq j \end{cases} \] -
当\(m \geq 1\)时,可以在\(I_{i , j}^{(m - 1)}\)的基础上计算从\(i\)到\(j\)的最多由\(m\)条边组成的任意路径的最小权重\(I_{i , j}^{(m)}\)。\(I_{i , j}^{(m - 1)}\)是从\(i\)到\(j\)最多由\(m- 1\)条边组成的最短路径的权重。
\(I_{i , j}^{(m)}\)的计算:通过对\(j\)的所有可能的前驱\(k\)进行检查获得
\(I_{i , j}^{(m)}\)的递归定义为:
结点间的最短路径权重\(\delta(i, j)\)
如果图\(G\)不包含权重为负值的环路,则对于每一对结点\(i\)和\(j\),如果\(\delta(i ,j) < \infin\),则从\(i\)到\(j\)之间存在一条最短路径。并且,由于最短路径是简单路径,其中至多包含\(n-1\)条边,因此有:
自底向上计算最短路径权重
\(I_{i , j}^{(1)}\)表示从结点\(i\)到结点\(j\)中间至多包含\(1\)条边的路径的最小权重,因此\(I_{i , j}^{(1)} = \omega_{i , j}\)。
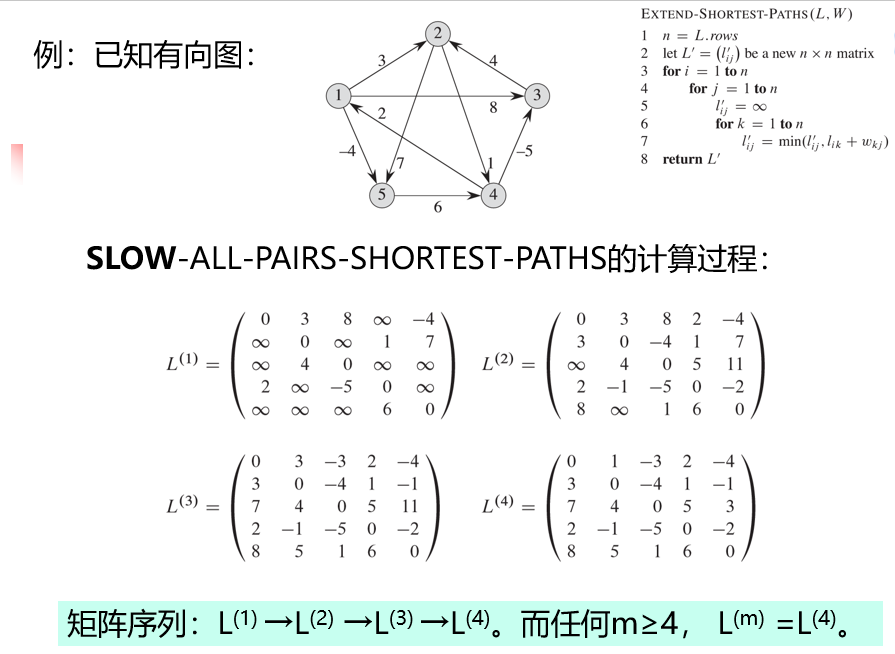
自底向上计算方法:根据输入矩阵\(W = (\omega_{i , j})\),计算\(L(1) = I_{i , j}^{(1)}\),然后根据递归关系式计算\(L(2) ,...,L(n - 1)\),其中:
\(L(n - 1)\)即是最后的最短路径权重结果矩阵,有\(I_{i , j}^{(n - 1)} =\delta(i , j)\)
伪代码:

算法将最近计算出的最短路径扩展一条边:找一条从\(i\)到某结点\(k\),再经过边\((k , j)\)到达\(j\)的更短路径。算法结束时返回结果矩阵\(L' = L(m)\)。时间复杂度:\(O(n^3)\)


Floyd-Warshall算法
现在讨论另一种动态规划策略来求解有向图的所有结点对最短路径问题-Floyd-Warshall算法
算法的时间复杂度是:\(O(|V|^3)\),算法允许图中存在负权重的边,但不能存在权重为负值的环路。
最短路径结构的重新描述:中间结点:一个简单路径\(p = <v_1 , v_2 , ...,v_k>\)上的中间结点是指路径\(p\)上除\(v_1\)和\(v_k\)之外的其它任意结点。
假定图\(G\)的结点集为\(V=\{1,2,…,n\}\)。考虑其中的一个子集\(\{1,2,…,k\}\),这里\(k\)是小于\(n\)的某个整数,并是其中的最大编号。对于任意一对结点\(i,j\in V\),定义\(p\)是从\(i\)到\(j\)、且所有中间结点均取自于集合\(\{1,2,…,k\}\)的最短路径。\(p\)是简单路径,且\(p\)的中间结点都不大于\(k\)。\(p\)从\(i\)到\(j\),仅经过集合\(\{1,2,…,k\}\)中的结点,但不一定经过其中的每一个结点,也可能不存在这样的路径,此时\(p\)的权重等于\(\infin\)。
状态转移方程:设\(d_{i , j}^{(k)}\)为从结点\(i\)到结点\(j\)的所有中间结点全部取自集合\(\{1 , 2 , ... , k\}\)的一条最短路径的权重,则有:
其中, \(k = 0\)时代表从结点\(i\)到结点\(j\)的一条不包含编号大于\(0\)的中间结点的路径,这样的路径没有任何中间结点,最多只有一条边,所以\(d_{i , j}^{(0)} = \omega_{i , j}\)。
而因为任何路径的中间结点都属于集合\(\{1 , 2 , ... , n\}\),所以\(k = n\)时,\(d_{i ,j}^{(n)}\)给出所有可能的从结点\(i\)到结点\(j\)的中间结点均取自集合\(\{1 , 2 , n\}\)的一条最短路径的权重,也就是从结点\(i\)到结点\(j\)的最短路径的权重。所以\(\forall i , j \in V\)有:\(d_{i , j}^{(n)} = \delta(i , j)\)。
矩阵\(D^{(n)} = (d_{i , j}^{(n)})\)为结果矩阵。

构建最短路径
在计算矩阵\(D^{(k)}\)的同时,计算前驱矩阵\(\prod\)序列:\(\prod^{(0)}、\prod^{(1)}...\prod^{(n)} = \prod\)。其中\(\pi_{i , j}^{(k)}\)为从结点\(i\)到结点\(j\)的一条所有中间结点都取自集合\(\{1 , 2 , ... , k\}\)的最短路径上\(j\)的前驱结点。当\(k = 0\)时:
\(k = 0\)时,是一条从\(i\)到\(j\)的没有中间结点的最短路径,所有当路径存在时\(\omega_{i , j} < \infin\), \(j\)的前驱就是\(i\)。
\(k \geq 1\)时:
举例:
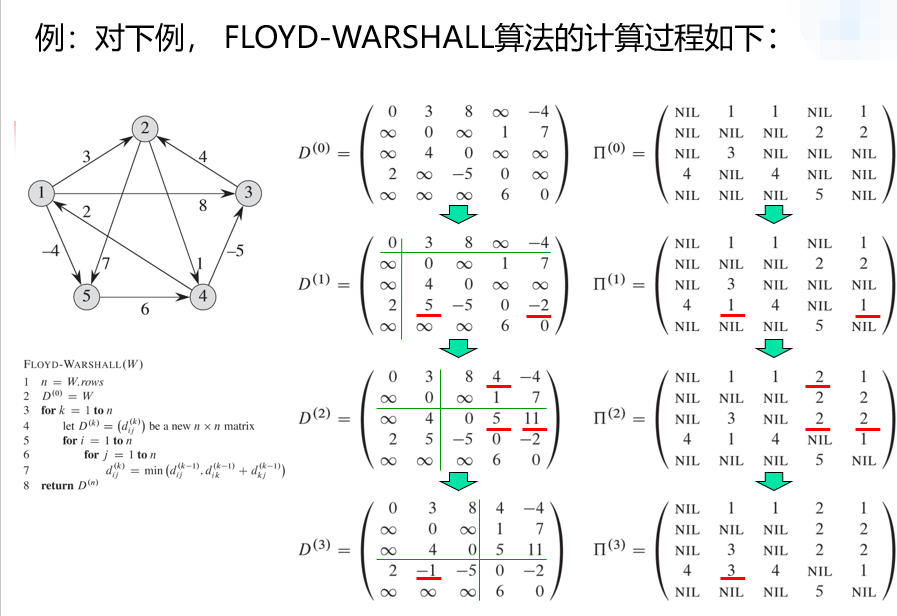
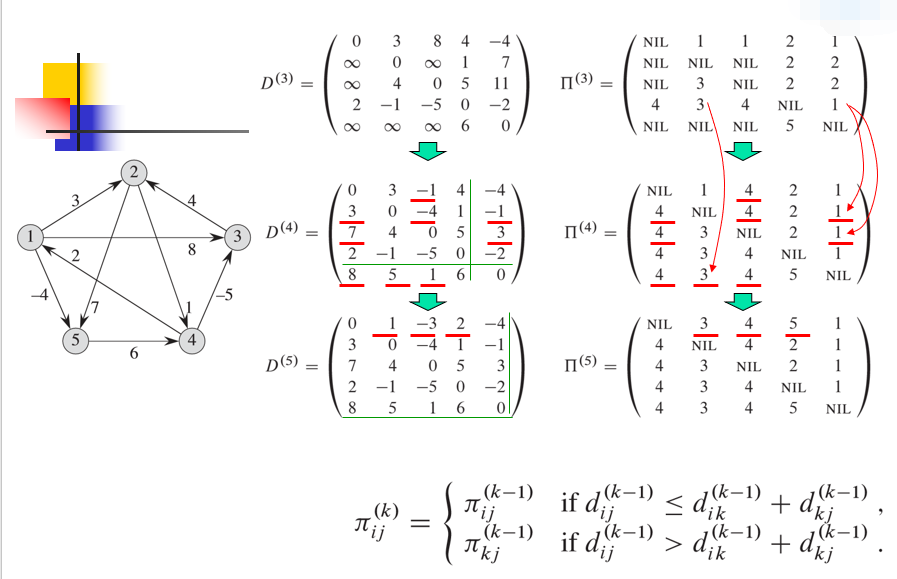
算法时间分析:\(3\)层嵌套的\(for\)循环,所用时间是\(\Theta(n^3)\)
有向图的传递闭包
定义有向图\(G=(V,E)\),定义图\(G\)的传递闭包\(G^*=(V,E^*)\),其中\(E^*=\{(i,j):如果图G中包含一条从结点i到结点j的路径\}\)。
求有向图的传递闭包:
方法一:给\(E\)中每条边赋权重\(1\),然后运行FLOYD-WARSHALL算法,可以在\(\Theta(n^3)\)求出权重路径矩阵\(D\)。在\(D\)中若\(d_{i ,j} < n\),则表示存在一条从结点\(i\)到结点\(j\)的路径,否则\(d_{i , j} = \infin\)。
方法二:定义矩阵\(T = \{t_{i , j}\}\) , 若存在一条从结点\(i\)到结点\(j\)的路径,\(t_{i , j} = 1\),否则\(t_{i , j} = 0\)。
计算T
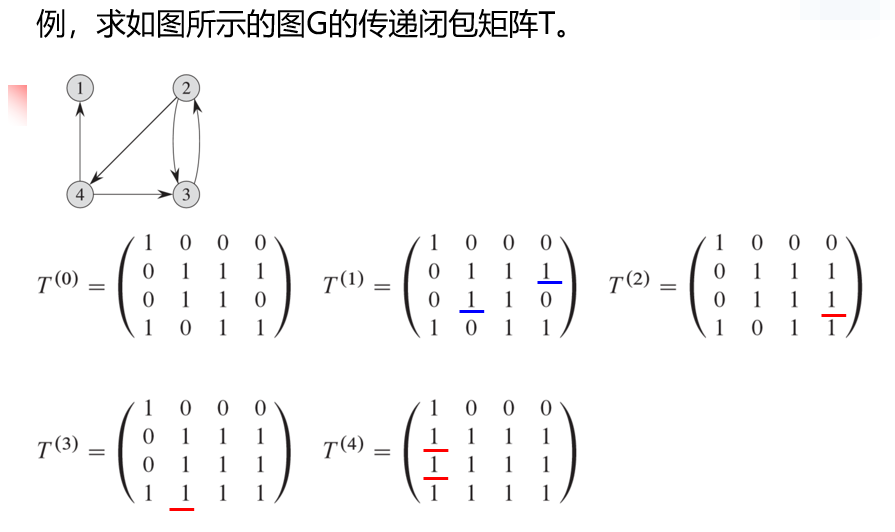
对FLOYD-WARSHALL算法进行改造:用逻辑或操作\(\or\)和逻辑与\(\and\) 替换算术操作\(min\)和\(+\),得到以下计算公式:
\(k = 0\)时:
\(k \geq 1\)时:
计算过程如下:

用于稀疏图的Johnson算法
用于有\(|V|\)个结点、\(|E|\)条边的有向图,求每对结点之间的最短路径
FLOYD-WARSHALL算法的时间复杂度为:\(\Theta(n^3)\)
用单源最短路径算法:执行\(|V|\)次单源最短路径算法,每次使用一个不同的结点作为源点,求出每个结点到其他所有结点的最短路径。
如果所有的边的权重为非负值,用Dijkstra算法。
- 用线性数组实现最小优先队列:\(O(V^3+VE)=O(V^3)\);
- 用二叉堆实现最小优先队列:\(O(VElogV)\);(对稀疏图较好)
- 用斐波那契堆实现最小优先队列:\(O(V^2logV+VE)\)
如果有权重为负值边,用Bellman-ford算法
- 一般的运行时间:\(O(V^2E)\)
- 对稠密图,运行时间为:\(O(V^4)\)
Johnson算法:在稀疏图中求每对结点之间的最短路径权重。
- 对稀疏图,Johnson算法优于Floyd-Warshall算法,时间复杂度可达\(O(V^2logV+VE)\)
- Johnson算法使用Dijkstra算法和Bellman-Ford算法作为自己的子程序,可处理带有负权重的图。
- 如果图中包含所有结点对的最短路径,Johnson算法输出一个包含所有结点对的最短路径权重矩阵;否则报告图中包含权重为负值的环路。
重赋权重
如果图\(G=(V,E)\)中所有的边权重\(\omega\)皆为非负值,则通过对每个结点运行一次Dijkstra算法来找到所有结点对之间的最短路径;
如果图\(G\)包含权重为负值的边,但没有权重为负值的环路,则通过重赋权重,构造出一组新的非负权重值,然后使用上面同样的方法求解(Dijkstra算法)。
新赋予的权重函数记为:\(\widehat{\omega}\),满足以下两个性质:
- 路径等价性:对于所有结点对\(u,v\in V\),一条路径p是在使用权重函数\(\omega\)时的从结点\(u\)到结点\(v\)的一条最短路径,当且仅当\(p\)是在使用权重\(\widehat{\omega}\)时的从\(u\)到\(v\)的一条最短路径。即不管是使用原来的权重函数还是新的权重函数,所能求出来的最短路径应是一致的。
- 非负性:对于所有的边\((u,v)\),新权重\(\widehat{\omega}(u , v)\)为非负值。即需要经过技术处理,把负权重的边的权重改造成非负值。
假设用\(\delta\)表示从权重函数\(\omega\)所导出的最短路径权重,用\(\widehat{\delta}\)表示从权重函数\(\widehat{\omega}\)所导出的最短路径权重。
引理(重新赋予权重并不改变最短路径) 给定带权重的有向图\(G = (V , E)\),其权重函数为\(\omega :E \to R\) , 设\(h: V \to R\)为任意函数,该函数将结点映射到实数上。对于每条边\((u , v) \in E\),定义:
设\(p = <v_0 , v_1 , ... , v_k>\)为从结点\(v_0\)到结点\(v_k\)的任意一条路径,那么\(p\)是在使用权重函数\(\omega\)时从结点\(v_0\)到结点\(v_k\)的一条最短路径,当且仅当\(p\)是在使用权重函数\(\widehat{\omega}\)时从结点\(v_0\)到结点\(v_k\)的一条最短路径,即:
并且图\(G\)在使用权重函数\(\omega\)时不包含权重为负值的环路。当且仅当\(p\)在使用权重函数\(\widehat{\omega}\)也不包含权重为负值的环路。
下证明\(\widehat{\omega}(p) = \omega(p) + h(u) - h(v)\):
根据定义,对于边有:\(\widehat{\omega}(u , v) = \omega(u ,v) + h(u) - h(v)\)
所以有:
因为\(h(v_0)\)和\(h(v_k)\)不依赖于任何具体路径,因此如果从结点\(v_0\)到结点\(v_k\)的一条路径在使用权重函数\(\omega\)时比另一条路径短,则在使用权重函数\(\widehat{\omega}\)时也比另一条短。故\(\omega(p) = \delta(v_0 , v_k)\)当且仅当\(\widehat{\omega}(p) = \widehat{\delta}(v_0 , v_k)\)。
再证明:并且图\(G\)在使用权重函数\(\omega\)时不包含权重为负值的环路。当且仅当\(p\)在使用权重函数\(\widehat{\omega}\)也不包含权重为负值的环路。
考虑任意环路\(c = <v_0 , v_1 , ..., v_k>\),其中\(v_0 = v_k\)。
因为
所以
因此环路\(c\)在使用权重函数\(\omega\)时为负当且仅当在使用权重函数\(\widehat{\omega}\)时也为负值。
下面寻找映射函数\(h\)
对于图\(G\)构造一个新图\(G' = (V' , E')\)其中\(V' = V \cup \{s\}\),\(s\)是一个新结点\(s \notin V\)。
\(E' = E \cup \{(s , v) : v \in V\}\),并令对于所有的结点\(v \in V\),有\(\omega(s , v) = 0\)。由于结点\(s\)没有入边,所以除了以\(s\)为源点的最短路径外,图\(G'\)中没有其它包含s的最短路径。而且\(G'\)不包含权重为负值的环路当且仅当图\(G\)不包含权重为负值的环路。
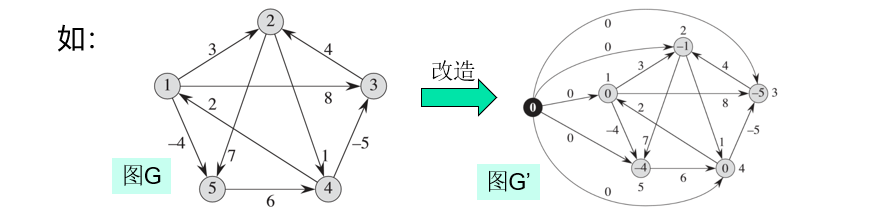
假定图\(G\)和图\(G'\)都不含有权重为负值的环路。对于所有的结点\(v \in V'\),定义:\(h(v) = \delta(s , v)\)。
根据三角不等式,对于所有的边\((u , v) \in E'\),有:
定义新权重\(\widehat{\omega}\),有
当对新图求出全源最短路径后,还原其实际路径长度:


- Johnson算法假定所有的边都保存在邻接表里。返回一个\(|V| \times |V|\)的矩阵\(D = (d_{i , j})\) ,其中\(d_{i , j} = \delta(i , j)\)。
- 或者报告图\(G\)中包含权重为负值的环路。
时间复杂度分析:
算法的运行时间依赖于Dijkstra算法中最小优先队列的实现方式:
- 如果使用斐波那契堆实现,则Johnson算法的运行时间为:\(O(V^2logV + VE)\)
- 如果使用二叉最小堆实现,则Johnson算法的运行时间为:\(O(VElogV)\)
- 在稀疏图的情况下,该算法的时间比Floyd-Warshall算法的表现要好
来道模板题:
P5905 【模板】Johnson 全源最短路
参考代码:
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define MAX 1000000000
using namespace std;
using PLI = pair<int, int>;
using ll = long long;
const int N = 3e3 + 5;
struct Node {
int v, w;
};
vector<vector<Node>>graph(N);
int n, m, u, v, w;
int h[N];
int read() {
int x = 0, f = 1;
char c = getchar();
for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
return x * f;
}
bool SPFA() {
memset(h, INF, sizeof(h));
queue<int>q;
vector<bool>vis(n + 1, false);
vector<int>cnt(n + 1, 0);
h[0] = 0; q.push(0);
while (!q.empty()) {
auto t = q.front(); q.pop();
vis[t] = false;
for(auto g : graph[t])
if (h[g.v] > g.w + h[t]) {
h[g.v] = g.w + h[t];
if (!vis[t]) {
if (++cnt[g.v] >= n + 1) return false;
vis[g.v] = true;
q.push(g.v);
}
}
}
return true;
}
void Dijkstra(int s , vector<int>& dis) {
dis[s] = 0;
vector<bool>vis(n + 1, false);
priority_queue<PLI, vector<PLI>, greater<PLI>>heap;
heap.push({ 0,s });
while (!heap.empty()) {
auto t = heap.top(); heap.pop();
int ver = t.second;
if (vis[ver]) continue;
vis[ver] = true;
for(auto g : graph[ver])
if (dis[g.v] > dis[ver] + g.w) {
dis[g.v] = dis[ver] + g.w;
heap.push({ dis[g.v] , g.v });
}
}
return;
}
int main() {
n = read(); m = read();
for (int i = 1; i <= m; ++i) {
u = read(); v = read(); w = read();
graph[u].push_back({ v , w });
}
for (int i = 1; i <= n; ++i) graph[0].push_back({ i,0 });
bool flag = SPFA();
if (!flag) {
cout << -1 << endl;
return 0;
}
for (int i = 1; i <= n; ++i)
for (auto& g : graph[i])
g.w = g.w + h[i] - h[g.v];
for (int i = 1; i <= n; ++i) {
vector<int>dis(n + 1, MAX);
Dijkstra(i, dis);
ll res = 0;
for (int j = 1; j <= n; ++j) {
if (dis[j] == MAX) res +=1ll * j * dis[j];
else res += 1ll* j * (dis[j] + h[j] - h[i]);
}
printf("%lld\n", res);
}
return 0;
}
作者:cherish.
出处:https://home.cnblogs.com/u/cherish-/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。

