单源最短路径

给定一个带权重的有向图\(G = (V , E)\) 和权重函数 \(\omega : E \to R\)。图中一条路径\(p= <v_0,v_1 , ...,v_k>\) 的权重 \(\omega(p)\)是构成该路径的所有边的权重之和：

\[\omega(p) = \sum_{i = 1}^{k} \omega(v_{i - 1} , v_i) \]

从结点\(u\)到结点\(v\)打最短路径权重\(\delta(u , v)\)定义如下：

\[\delta(u , v) = \begin{cases} min \{\omega(p):u \overset{p}\leadsto v\} & if\;there\;is\;a\;path\;from\;u\;to\;v\\ \infin & otherwise \end{cases} \]

单源最短路径问题

问题描述：给定一个图\(G=(V , E)\)，找出从给定的源点\(s \in V\)到其它每个结点\(v \in V\)的最短路径。

• 最优路径的最优子结构

  这样最短路径具有最优子结构性：两个结点之间的最短路径的任何子路径都是最短的。

  引理24.1 ： 给定一个带权重的有向图\(G=(V,E)\)和权重函数\(\omega:E\to R\)。设\(p=<v_0,v_1,…,v_k>\)为从结点\(v_0\)到结点\(v_k\)的一条最短路径，\(\forall i , j , 0\leq i \leq j\leq k\)，设\(p_{i , j}=<v_i,v_{i+1},…,v_j>\)为路径\(p\)中从结点\(v_i\)到结点\(v_j\)的子路径，则\(p_{i,j}\)是从结点\(v_i\)到结点\(v_j\)的一条最短路径。（证明略，见算法导论P375）

• 负权重的边

  权重为负值的边称为负权重的边，如果存在负权重的边，则有可能存在权重为负值的环路，而造成图中最短路径无定义（路径的权重为\(-\infin\) ）。

  

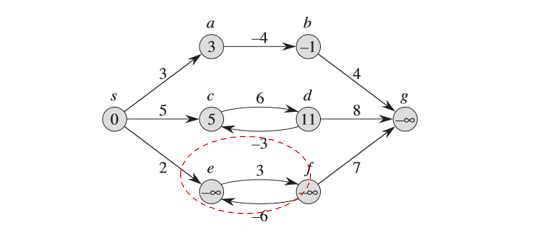
• 环路

  最短路径不应包含环路；不包含环路的路径称为简单路径。对任何简单路径最多包含\(|V| - 1\)条边和\(|V|\)个结点。不失一般性，假设后续算法寻找的最短路径都不包含环路。

• 最短路径的表示

  一个结点的前驱结点记为：\(v.\pi\)。前驱结点或者为\(NIL\)或者为另一个结点。利用\(v.\pi\)的记录可以搜索出最短路径上的所有结点。

• 前驱子图

  定义前驱子图为\(G_{\pi} = (V_{\pi} , E_{\pi})\)，其中，结点集合\(V_{\pi} = \{v \in V : v.\pi \neq NIL\} \cup \{s\}\)。即\(V_{\pi}\)是图\(G\)中的前驱结点不为\(NIL\)的结点的集合，再加上源点\(s\)；边集合\(E_{\pi} = \{(v.\pi , v) \in E : v \in V_{\pi} - \{s\}\}\),即\(E_{\pi}\)是由\(V_{\pi}\)中的结点的\(\pi\)值所诱导的边的集合。则算法终止时，\(G_{\pi}\)是一棵最短路径树，该数包含了从源结点\(s\)到每个可以从\(s\)到达的结点的一条最短路径。

设\(G =(V , E)\)是一个带权重的有向图，其权重函数为：\(\omega : E \to R\),假定\(G\)不包含从\(s\)可以到达的权重为负值的环路（无负环），因此所有的最短路径都有定义。

一棵根结点为\(s\)的最短路径树是一个有向子图\(G' = (V' , E')\)，其中\(V' \subseteq V , E' \subseteq E\)。具有以下性质：

• \(V'\)是图\(G\)中从源结点\(s\)可以到达的所有结点的集合。
• \(G'\)形成一棵根结点为\(s\)的树。
• 对于所有的结点\(v \in V'\)，图\(G'\)中从结点\(s\)到结点\(v\)的唯一简单路径是图\(G\)中从结点\(s\)到结点\(v\)的一条最短路径。（因为从源结点到目标结点的最短路径可能不止一条所以这里说是其中一条）

松弛操作（Relax）

对于每个结点\(v\)，维持一个属性\(v.d\)，记录从源点\(s\)到结点\(v\)的最短路径权重的上界。称\(v.d\)为\(s\)到\(v\)的最短路径估计。

松弛操作：首先测试一下是否可以对从\(s\)到\(v\)的最短路径进行改善（即有没有更短的路径）。如果可以改善，则\(v.d\)更新为新的最短路径估计值，\(v\)的前驱\(v.\pi\)更新为新的前驱结点。

最短路径和松弛操作的性质

• 三角不等式的性质

  引理24.11：设\(G=(V , E)\)为一个带权重的有向图，其权重函数为\(\omega : E \to R\),设其源结点为\(s\)。那么对于所有的边\((u , v) \in E\)，有：

  \[\delta(s , v) \leq \delta(s , u) + \omega(u , v) \]

  证明：假定\(p\)是从源结点\(s\)到结点\(v\)的一条最短路径，则\(p\)的权重不会比任何从\(s\)到\(v\)的其它路径的权重大，因此路径\(p\)的权重也不会比这样的一条路径的权重大：从源结点\(s\)到结点\(u\)的一条最短路径，再加上边\((u , v)\)而到达结点\(v\)的这条路径。如果\(s\)到\(v\)没有最短路径，则不可能存在到\(v\)的路径。

• 上界性质：\(v.d\)是\(s\)到\(v\)的最短路径权重\(\delta(s , v)\)的上界

  引理：设\(G=(V,E)\)为一个带权重的有向图，其权重函数为\(\omega:E \to R\)，设其源结点为\(s\)，该图由算法 INITIALIZE-SINGLE-SOURCE(G,s) 执行初始化。那么对于所有的结点\(v\in V，v.d\geq \delta(s,v)\)。并且该不变式在对图\(G\)的边进行任何次序的松弛过程中都保持成立，而一旦\(v.d\)取得其下界\(\delta(s,v)\)后，将不再发生变化。

  用数学归纳法证明：对于所有的结点\(v \in V , v.d \geq \delta(s , v)\)(归纳的主体是松弛步骤的数量)

  基础步：在经INITIALIZE-SINGLE-SOURCE(G,s) 初始化之后，对于所有的结点\(v \in V - \{s\}\)，置\(v.d= \infin\)，而\(s.d=0\) ，显然\(s.d \geq \delta(s,s)\)，而其它的结点 \(v.d\geq \delta(s,v)\)，结论成立。

  归纳步：考虑对边\((u , v)\)的松弛操作。归纳假设：在对边\((u , v)\)进行松弛之前，对所有的结点\(x \in V , x.d \geq \delta(s , x)\)。而在对边\((u , v)\)进行松弛的过程中，唯一可能发生改变的\(d\)值只有\(v.d\)，如果该值发生变化，则有：

  \[v.d = u.d + \omega(u , v)\\ \geq \delta(s , u) + \omega(u , v) \\ \geq \delta(s , v) \]

  同理，根据计算的规则，在\(v.d\)达到其下界\(\delta(s , v)\)后，就无法再减小也不能增加。

  引理得证

• 非路径性质

  推论：给定一个带权重的有向图\(G=(V,E)\)，其权重函数为\(\omega:E \to R\)。假定从源结点\(s\)到给定点\(v\)之间不存在路径，则该图在由算法 INITIALIZE-SINGLE-SOURCE(G,s) 进行初始化后，有 \(v.d\geq δ(s,v)=\infin\)。并且该等式作为不变式一直维持到图\(G\)的所有松弛操作结束。

  证明：因为从源点\(s\)到给定点\(v\)之间不存在路径，所以\(\delta(s , v) = \infin\)。而根据上界性质，总有\(v.d \geq \delta(s , v)\) ， 所以\(v.d \geq \delta(s , v) = \infin\)。得证

  引理：设\(G=(V,E)\)为一个带权重的有向图，其权重函数为\(\omega:E\to R\)，并且边\((u,v)\in E\)。那么在对边\((u,v)\)进行松弛操作\(RELAX(u,v,ω)\)后，有\(v.d\leq u.d+\omega(u,v)\)。

  证明：如果在对边\((u,v)\)进行松弛操作前，有\(v.d>u.d+\omega(u,v)\)，则松弛操作时，置\(v.d=u.d+\omega(u,v)\)。如果在松弛操作前有\(v.d\leq u.d+\omega(u,v)\)，则松弛操作不会改变\(v.d\)和\(u.d\)的值，因此在松弛操作后仍有\(v.d\leq u.d+\omega(u,v)\) 。得证。

• 收敛性质

  引理：设\(G=(V,E)\)为一个带权重的有向图，其权重函数为\(\omega:E\to R\)。设\(s\in V\)为某个源结点,\(s \leadsto u \to v\)为图\(G\)中的一条最短路径\((u，v\in V)\)。 假定图\(G\)由算法INITIALIZE-SINGLE-SOURCE(G,s)进行初始化，并在这之后进行了一系列边的松弛操作，其中包括对边\((u,v)\)的松弛操作RELAX(u,v,ω)。如果在对边\((u,v)\)进行松弛操作之前的某时刻有\(u.d=\delta(s,u)\)，则在该松弛操作之后的所有时刻有\(v.d=\delta(s,v)\) 。

  证明：

  根据上界性质，如果在对边\((u , v)\)进行松弛前的某个时刻有\(u.d = \delta(s , u)\)，则该等式在松弛之后仍然成立。特别地，在对边\((u , v)\)进行松弛之后，有：

  \[v.d \leq u.d + \omega(u , v) \\ = \delta(s , u) + \omega(u , v)\\ = \delta(s , v) \]

  而根据上界性质\(v.d \geq \delta(s , v)\)。所以有\(v.d = \delta(s , v)\),并且该等式在此之后一直保持成立。得证。

• 路径松弛性质

  引理：设\(G=(V,E)\)为一个带权重的有向图，其权重函数为\(\omega:E\to R\)。设\(s\in V\)为某个源结点，考虑从源结点\(s\)到结点\(v_k\)的任意一条最短路径\(p=<v_0,v_1,…,v_k>\),\(v_0=s\)。如果图\(G\)由算法 INITIALIZE-SINGLE-SOURCE(G,s) 进行初始化，并在这之后进行了一系列边的松弛操作，其中包括对边\((v_0,v_1)、 (v_1,v_2)、…、 (v_{k-1},v_k)\)按照所列次序而进行的松弛操作，则在所有这些松弛操作之后，有\(v_k.d=δ(s,v_k)\)，并且在此之后该等式一直保持。 该性质的成立与其他边的松弛操作及次序无关，即使这些松弛操作是与对\(p\)上的边所进行的松弛操作穿插进行的。

  归纳法证明：在最短路径\(p\)的第\(i\)条边被松弛之后，有\(v_i.d = \delta(s , v_i)\)

  基础步：在对路径\(p\)的任何一条边进行松弛操作之前，从初始化算法可以得出：\(v_0.d=s.d=\delta(s,s)\)。结论成立，且\(s.d\)的取值在此之后不再发生变化。

  归纳步：假定依次经过\((v_0,v_1)、 (v_1,v_2)、…、 (v_{i-2},v_{i-1})\)松弛操作之后，\(v_{i-1}.d=\delta(s,v_{i-1})\)。则在对边\((v_{i-1},v_i)\)进行松弛操时，根据收敛性质，必有在对该边进行松弛后\(v_i.d=\delta(s,v_i)\)，并且该等式在此之后一直保持成立。得证。

Bellman-ford算法

Bellman-ford算法可以求解一般情况下的单源最短路径问题，即可以有负权重的边，但不能有负权重的环。

设\(G = (V , E)\)为一个带权重的有向图，其权重函数为\(\omega:E \to R\)。\(s \in V\)为源结点。

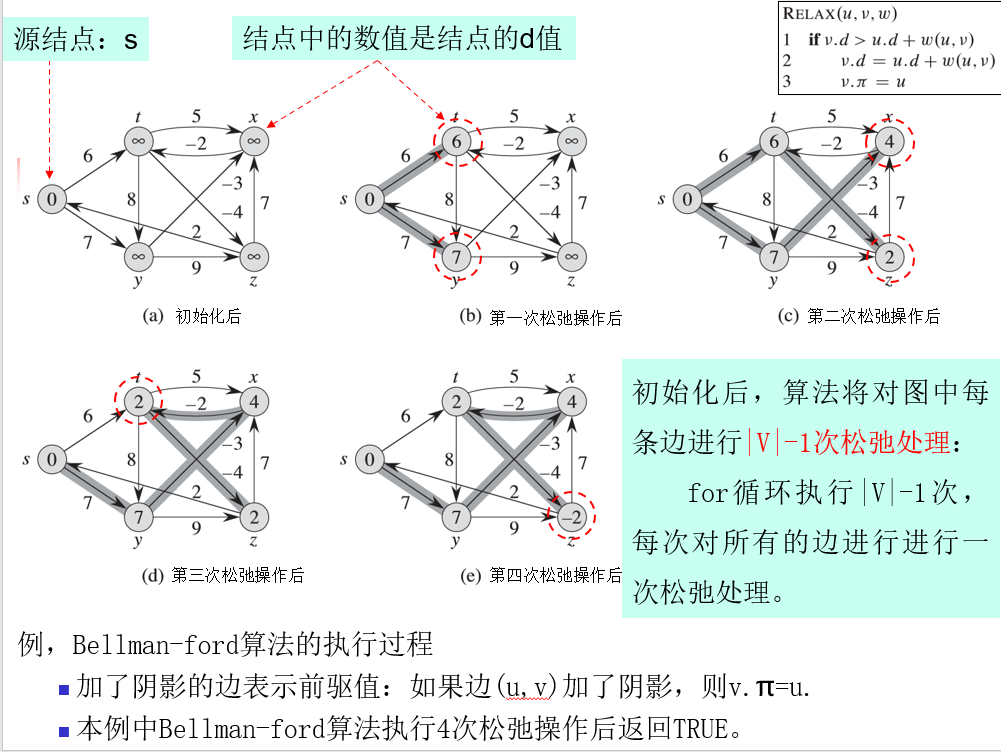
Bellman-ford算法的时间复杂度：初始化\(\Theta(V)\) ， 松弛操作：for循环执行\(|V| - 1\)次每次的时间是\(\Theta(E)\)，故总的时间复杂度是：\(O(VE)\)

关于算法正确性的证明不在此赘述

Bellman-ford算法检查图中可能存在的负权重回路的方法：在进行\(|V|-1\)次迭代之后再进行一次迭代操作，如果这次操作后的最短路径值与上一次的不一样，就说明存在负权重回路。

证明： 假定图\(G\)包含一个权重为负值的环路，并且该环路可以从源结点s到达。设该环路为\(c=<v_0,v_1,…v_k>\)，这里\(v_0=v_k\)。因为环路的权重为负值，所以有：\(\sum\limits_{i = 1}^{k} \omega(v_{i - 1} , v_i) < 0\)

反正法证明：假设这次迭代操作后最短路径不变，则有\(v_i.d \leq v_{i - 1}.d + \omega(v_{i - 1} , v_i)\)

将环路\(c\)上的所有这种不等式都加起来，有：

\[\sum\limits_{i = 1}^{k}v_i.d \leq \sum\limits_{i = 1}^k (v_{i - 1}.d + \omega(v_{i - 1} , v_i))\\ = \sum\limits_{i = 1}^k v_{i - 1}.d + \sum\limits_{i = 1}^k \omega(v_{i -1} , v_i) \]

由于\(v_0 = v_k\)，环路\(c\)上面的每个结点在上述求和表达式\(\sum\limits_{i=1}^k v_i.d\) 和\(\sum\limits_{i = 1}^kv_{i - 1}.d\)中都刚好各出现一次。因此有：

\[\sum\limits_{i =1}^k v_i.d = \sum\limits_{i = 1}^kv_{i - 1}.d\\ 0 \leq \sum\limits_{i = 1}^{k} \omega(v_{i - 1} , v_i) \]

与\(\sum\limits_{i = 1}^k \omega(v_{i - 1} , v_i) < 0\)矛盾。

故如果图\(G\)中不包含从源结点\(s\)可以到达的权重为负值的环路，则算法多进行一次迭代操作不会使最短路发生改变，否则会使最短路发生改变。

Dijkstra算法

Dijkstra算法解决带权重的有向图上单源最短路径问题。该算法要求所有边的权重均为非负值，即对于所有的边\((u , v) \in E , \omega(u , v) \geq 0\)，不能有负权重的边和负环。

Dijkstra算法是一个贪心算法：每次总是选择\(V-S\)集合中最短路径估计值最小的结点加入\(S\)中。

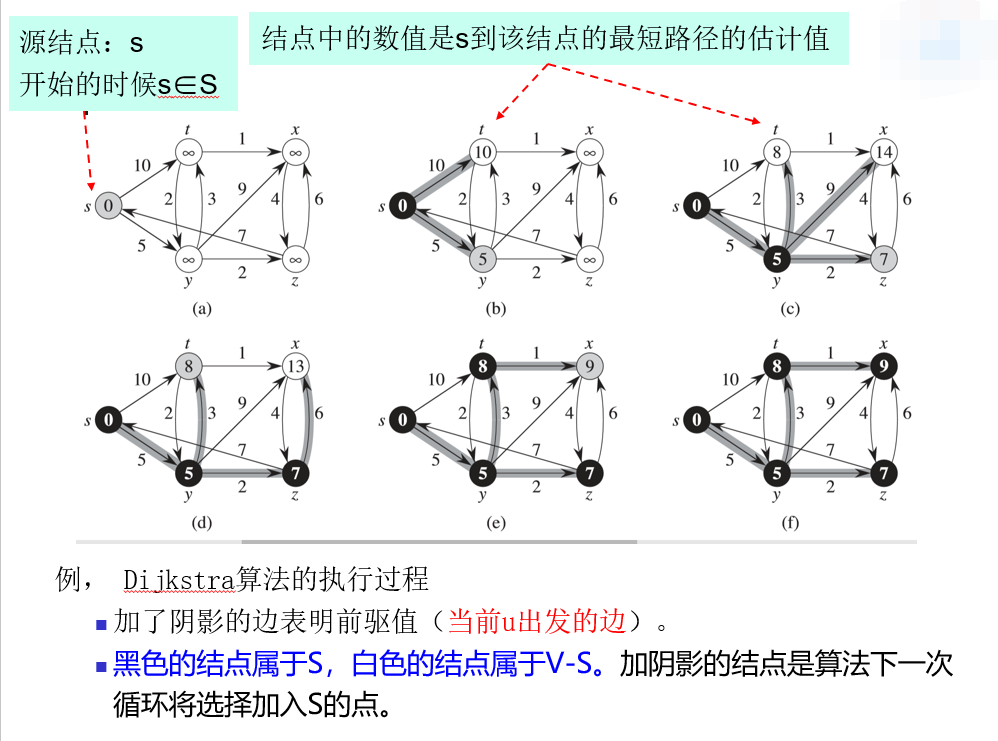
算法正确性证明不在此赘述。

Dijkstra算法时间复杂度分析：根据算法的处理规则，每个结点\(u\)仅被加入集合\(S\)一次，邻接链表\(Adj[u]\)中的每条边在整个运行期间也只被检查一次。因此算法第7-8行(伪代码)的for循环执行次数总共为|E|次（即松弛判定总次数）。

Dijkstra算法的总运行时间依赖于最小优先队列Q的实现:

• 如果用线性数组(无序或者按序插入)实现，每次找\(d\)最小的结点\(u\)需要\(O(V)\)的时间，所以算法的总运行时间为\(O(V^2+E)=O(V^2)\)。
• 如果用二叉堆实现，每次找\(d\)最小的结点\(u\)需要\(O(logV )\)的时间，所以算法的总运行时间为\(O((V+E)logV)\)。
• 如果用斐波那契堆实现，算法的总运行时间可以改善至\(O(VlogV+E)\)。（没用过）

这里放前两个的实现：

P3371 【模板】单源最短路径（弱化版）

题目描述：模板题，数据范围：\(1 \leq n \leq 10^4\)， \(n^2\)可过。

参考代码：

#include<bits/stdc++.h>
#include<unordered_map>
using ll = long long;
using namespace std;
#define PII pair<int,int>
struct Node {
	int v, w;
};
int read() {
	int x = 0, f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - 48;
	return x * f;
}
int n, m, s, u, v, w;
int main() {
	n = read(); m = read(); s = read();
	vector<int>ans(n + 1, INT_MAX);
	vector<vector<Node>>a(n + 1);
	vector<bool>vis(n + 1, false);
	Node b;
	ans[s] = 0;
	while (m--) {
		u = read(); v = read(); w = read();
		b.v = v, b.w = w;
		a[u].push_back(b);
	}
	int mx = INT_MAX;
	while (!vis[s]) {
		vis[s] = true;
		for (auto an : a[s])
			if (!vis[an.v] && ans[an.v] > ans[s] + an.w) ans[an.v] = ans[s] + an.w;
		mx = INT_MAX;
		for (int i = 1; i <= n; ++i)
			if (!vis[i] && mx > ans[i]) mx = ans[i], s = i;
	}
	for (int i = 1; i <= n; ++i) cout << ans[i] << " ";
	return 0;
}

P4779 【模板】单源最短路径（标准版）

题目描述：模板题。数据范围\(1 \leq n \leq 10^5\)。使用二叉堆实现可过。

参考代码：

#include<bits/stdc++.h>
#include<unordered_map>
using ll = long long;
using namespace std;
#define PII pair<int,int>
struct Node {
	int v, w;
};
int read() {
	int x = 0, f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -1;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - 48;
	return x * f;
}
int n, m, s, u, v, w;
priority_queue<PII, vector<PII>, greater<PII>>heap;
int main() {
	n = read(); m = read(); s = read();
	vector<int>ans(n + 1, INT_MAX);
	vector<vector<Node>>a(n + 1);
	vector<bool>vis(n + 1, false);
	Node b;
	ans[s] = 0;
	while (m--) {
		u = read(); v = read(); w = read();
		b.v = v, b.w = w;
		a[u].push_back(b);
	}
	heap.push({ 0,s });
	while (!heap.empty()) {
		auto t = heap.top();
		heap.pop();
		int ver = t.second, distance = t.first;
		if (vis[ver]) continue;
		vis[ver] = true;
		for (auto an : a[ver])
			if (ans[an.v] > distance + an.w) {
				ans[an.v] = distance + an.w;
				heap.push({ ans[an.v],an.v });
			}
	}
	
	for (int i = 1; i <= n; ++i) cout << ans[i] << " ";
	return 0;
}

存在负权边使Dijkstra算法工作异常的例子：考虑\(3\)个结点\(1 ,2 , 3\)，\(\omega(1 , 2) = 4 , \omega(1 , 3) = 5 , \omega(3 , 2) = -3\) 寻找从\(1 \to 2\)的最短路，上述算法跑出来是\(1\to 2\)，实际是\(1\to 3 \to 2\)。

差分约束和最短路径

线性规划：给定一个\(m\times n\)的矩阵\(A\)、一个\(m\)维的向量\(b\)和一个\(n\)维的向量\(c\)。试找一\(n\)维向量\(x\)，使得在\(Ax\leq b\)的约束下，目标函数\(\sum\limits_{i = 1}^n c_ix_i\)最大。

现讨论线性规划的一个特例：差分约束系统。

差分约束系统：在一个差分约束系统中，线性规划矩阵\(A\)的每一行包括一个\(1\)和一个\(-1\)，其它所有项皆为\(0\)。由\(Ax \leq b\)给出的约束条件形式上是\(m\)个设计\(n\)个变量的差额限制条件，每个约束条件是以下简单的线性不等式关系：

\[x_j - x_i \leq b_k\;1 \leq i , j \leq n , i \neq j , 1 \leq k \leq m \]

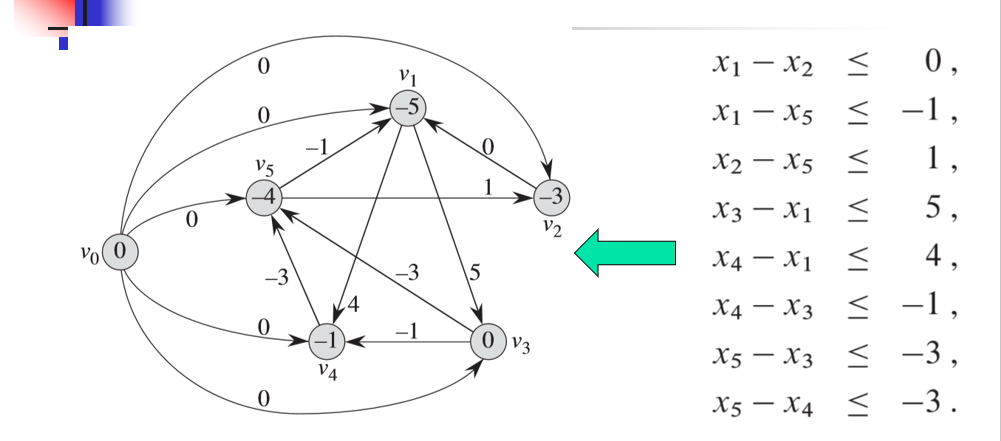
例：一个满足下列条件的\(5\)维向量\(x= (x_i)\)的问题

\[\left[ \begin{matrix} 1 & -1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & -1\\ 0 & 1 & 0 & 0 & -1\\ -1 & 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 1 & 0\\ 0 & 0 & -1 & 1 & 0\\ 0 & 0 & -1 & 0 & 1\\ 0 & 0 & 0 & -1 & 1\\ \end{matrix}\right] \left[ \begin{matrix} x_1\\x_2\\x_3\\x_4\\x_5 \end{matrix}\right] \leq \left[ \begin{matrix} 0\\-1\\1\\5\\4\\-1\\-3\\-3 \end{matrix}\right] \]

一般形式为：

\[x_1 - x_2 \leq 0 \\ x_1 - x_5 \leq -1 \\ x_2 - x_5 \leq 1 \\ x_3 - x_1 \leq 5 \\ x_4 - x_1 \leq 4 \\ x_4 - x_3 \leq -1 \\ x_5 - x_3 \leq -3 \\ x_5 - x_4 \leq -3 \\ \]

找一组满足上述约束条件的解。

问题的可能答案有：\(x= (-5 , -3 , 0 , -1 , -4)、x= (0 , 2 , 5 , 4 , 1)\)等多组可行解。

引理：设向量\(x=(x_1,x_2,…,x_n)\)为差分约束系统\(Ax\leq b\)的一个解，设\(d\)为任意常数，则\(x+d=(x_1+d,x_2+d,…, x_n+d)\)也是个该差分约束系统的一个解。

证明:根据约束条件，对每对\(x_i\)和\(x_j\)，\((x_i+d)-(x_j+d)=x_i-x_j\)。因此若向量\(x\)满足\(Ax\leq b\)，则向量\(x+d\)也满足\(Ax\leq b\)。

约束图

在一个\(Ax\leq b\)的差分约束系统中，将\(m\times n\)的矩阵\(A\)看成是一张有\(n\)个结点和\(m\)条边构成的图的邻接矩阵的转置。

约束图定义如下：对给定的差分约束系统\(Ax\leq b\)，其对应的约束图是一个带权重的有向图\(G=(V,E)\)，这里\(V = \{v_0 , v_1 , v_2 , ... , v_n\}\) 。\(E = \{(v_i , v_j) : x_j - x_i \leq b_k\} \cup \{(v_0 , v_1) , ... , (v_0 , v_n)\}\)

每条有向边对应一个不等式，\((v_0,v_i)\)是从新增的\(v_0\)到其他所有结点的边。

说明：

• 结点集合：约束图中引入一个额外的结点\(v_0\)，从其出发可以达到其他所有结点。因此结点集合\(V\)由代表每个变量\(x_i\)的结点\(v_i\)和额外的结点\(v_0\)组成。
• 边集合：边集合\(E\)包含代表每个差分约束的边，同时包含\(v_0\)到其他所有结点的边\((v_0,v_i)\;\forall 1 \leq i \leq n\)。
• 边的权重：如果\(x_j-x_i \leq b_k\)是一个差分约束条件，则边\((v_i,v_j)\)的权重记为\(\omega(v_i,v_j) = b_k\)，而从\(v_0\)出发到其他结点的边的权重\(\omega(v_0,v_j)=0\)。

定理:给定差分约束系统\(Ax \leq b\)，设\(G=(V,E)\)是该差分约束系统所对应的约束图。

• 如果图\(G\)不包含权重为负值的回路，则\(x = (\delta(v_0 , v_1) , ...,\delta(v_0 , v_n))\)是该系统的一个可行解。
• 如果图\(G\)包含权重为负值的回路，则该系统没有可行解。

证明：考虑任意一条边\((v_i , v_j) \in E\)，根据三角不等式有：

\[\delta(v_0 , v_j) \leq \delta(v_0 , v_i) + \omega(v_i ,v_j)\\ \delta(v_0 , v_j) - \delta(v_0 , v_i) \leq \omega(v_i , v_j) \]

因此令\(x_i = \delta(v_0 , v_i) , x_j = \delta(v_0 , v_j)\),则\(x_i , x_j\)满足对应边\((v_i , v_j)\)的差分约束条件\(x_j - x_i \leq \omega(v_i , v_j) = b_k\) 。因此\(x = (\delta(v_0 , v_1) , ...,\delta(v_0 , v_n))\)是问题的一个可行解。（前提：不包含权重为负的环路）

而如果约束图包含权重为负值的环路，不失一般性，设权重为负值的环路为\(c = <v_1 , v_2 , v_k>\)，其中\(v_1 = v_k\)。环路\(c\)对应下面的差分约束条件：

\[x_2 - x_1 \leq \omega(v_1 , v_2)\\ x_3 - x_2 \leq \omega(v_2 , v_3)\\ .\\ .\\ .\\ x_{k - 1} - x_{k - 2} \leq \omega(v_{k - 2} , v_{k - 1})\\ x_k - x_{k - 1} \leq \omega(v_{k - 1} , v_k)\\ \]

不等式左侧求和等于\(0\)，不等式右侧求和等于环路\(c\)的权重\(\omega(c)\),且有：\(0 \leq \omega(c)\),这与\(c\)的权重为负值相矛盾，故该组不等式无解。

求解差分约束系统

可以使用Bellman-Ford算法来求解差分约束系统。约束图中含有从源结点\(v_0\)到其他所有结点的边,若存在权重为负值的环路，则都可以从结点\(v_0\)到达。则:

• 如果Bellman-Ford算法返回TRUE，则最短路径权重\(\delta(v_0,v_i)\;\forall 1 \leq i \leq n\),给出该系统的一个可行解。
• 如果算法返回FALSE，则该系统无解。