子集和数问题

问题描述：
已知\(n\)个正数的集合\(W={w_1, w_2, …, w_n}\)和正数\(M\)。找出\(W\)中的和数等于\(M\)的所有子集。

例： \(n＝4,W = (w_1,w_2,w_3,w_4)＝(11，13，24，7), M=31\)。则满足要求的子集有：

• 直接用元素表示：\((11,13,7)\)和\((24,7)\)

• \(k\)-元组（用元素下标表示）：\((1,2,4)\)和\((3,4)\)

• \(n\)-元组（用n元向量表示）：\((1,1,0,1)\)和\((0,0,1,1)\)

状态空间生成树：

• 元组大小固定：\(n\)元组\((x_1 , x_2 , ...,x_n)，\forall 1 \leq i \leq n , x_i = 0 \;or\;x_i = 1\)。表示选第\(i\)个数或者不选第\(i\)个数

• 结点：对于\(i\)级上的一个结点，其左儿子对应于\(x_i = 1\)，右儿子对应于\(x_i = 0\).

• 限界函数的选择：

  约定：\(w_i\)按照非降次序排列

  条件一：\(\sum_{i = 1}^k w_ix_i + \sum_{i = k + 1}^n w_i \geq M\)

  条件二：\(\sum_{i = 1}^{k}w_ix_i + w_{k + 1} \leq M\)

  仅当满足上述两个条件时，限界函数\(B(x_1 , x_2 , ...,x_k) = true\)

伪代码：

实例：

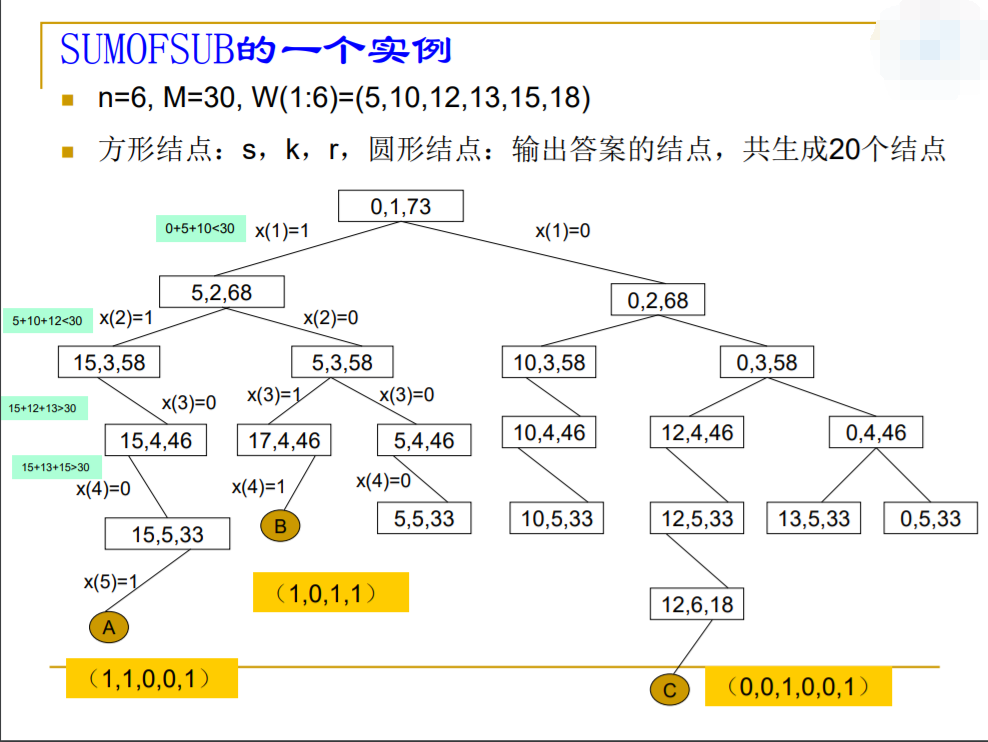
看看图就好了，学会怎么做就行，推荐几道可能相关的习题，当然实际做法不一定像上面那样做，因为每个数只有选或者不选两种状态，所以可以考虑使用搜索枚举所有可能情况，时间复杂度为:\(O(2^n)\)

78. 子集

90. 子集 II

494. 目标和

参考代码：

class Solution {
public:
    int ans=0; 
    int findTargetSumWays(vector<int>& nums, int sum) {
        dfs(0,nums,(long long)sum);
        return ans;
    }
    void dfs(int curr,vector<int>& nums , long long sum){
        if(curr==nums.size()){
            if(sum==0) ans++;
            return ;
        }
        dfs(curr+1,nums,sum-nums[curr]);
        dfs(curr+1,nums,sum+nums[curr]);
    }
};