Huffman编码

背景：需要压缩一个有\(10\)万个字符的数据文件。

分析：采用二进制字符编码，每个字符用唯一的二进制串表示，称为码字。

• 定长编码：每个字符的长度一样。考虑有六个字符的数据文件，可使用\(3\)位码字对每个字符编码，\(10\)万个字符需要用\(30\)万个二进制位来对文件编码。
• 变长编码：每个字符赋予不同长度的码字。赋予高频字符短码字，低频字符长码字，字符的码字互不为前缀，这样才能唯一解码。

最优编码方案的设计

一些定义：

前缀码：任何码字都不是其它码字的前缀。

文件编码过程：将文件中的每个字符的码字连接起来即可完成文件的编码过程。

文件解码过程：前缀码可以简化解码过程：由于没有码字是其它码字的前缀，所以编码文件的开始部分是没有歧义的，可以唯一地转换回原字符，然后对编码文件剩余部分重复解码过程，即可“解读”出原来的文件。

编码树：一种为表示字符二进制编码而构造的二叉树。

叶子结点：对应给定的字符，每个字符对应一个叶子结点。

编码构造：字符的二进制码字由根结点到该字符叶子结点的简单路径表示：\(0\)代表转向左孩子，\(1\)代表转向右孩子。

一个文件的最优字符编码方案总对应一棵满二叉树，即每个非叶子结点都有两个孩子结点。

• 设\(C\)为字母表
  • 对字母表\(C\)中的任意字符\(c\)，令属性\(c.freq\)表示字符\(c\)在文件中出现的频率（设所有字符的出现频率均为正数）。
  • 最优前缀码对应的树中恰好有\(|C|\)个叶子结点，每个叶子结点对应字母表中的一个字符，且恰有\(|C|-1\)个内部结点。
• 令\(T\)表示一棵前缀编码树
• 令\(d_T(c)\)表示\(c\)的叶子结点在树\(T\)中的深度（根到叶子结点的路径长度），也是字符\(c\)的码字的长度。
• 令\(B(T)\)表示采用编码方案\(T\)时文件的编码长度，则\(B(T) = \sum_{c \in C} f.freq \times d_T(c)\)
• 称\(B(T)\)为\(T\)的代价（文件需要用\(B(T)\)个二进制位表示）。
• 最优编码：使得\(B(T)\)最小的编码称为最优编码。对给定的字符集和文件，Huffman编码是一种最优的编码。

Huffman编码的贪心算法

算法HUFFMAN从\(|C|\)个叶子结点开始，每次选择频率最低的两个结点合并，将得到的新结点加入集合继续合并，这样执行\(|C|-1\)次“合并”后即可构造出一棵编码树——Huffman树。

伪代码：

实例：


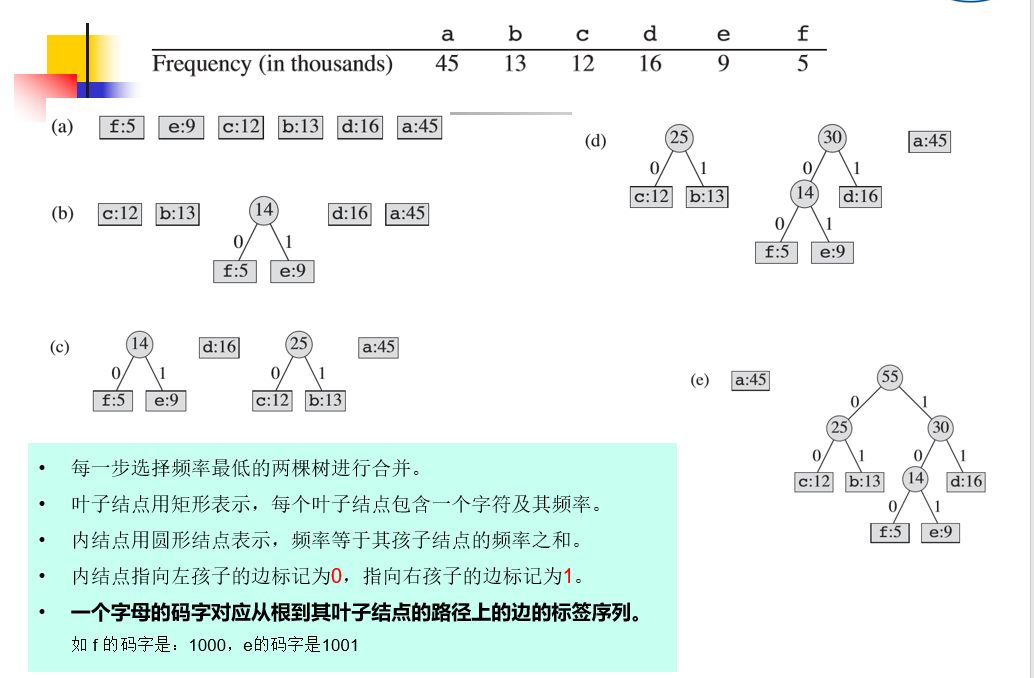
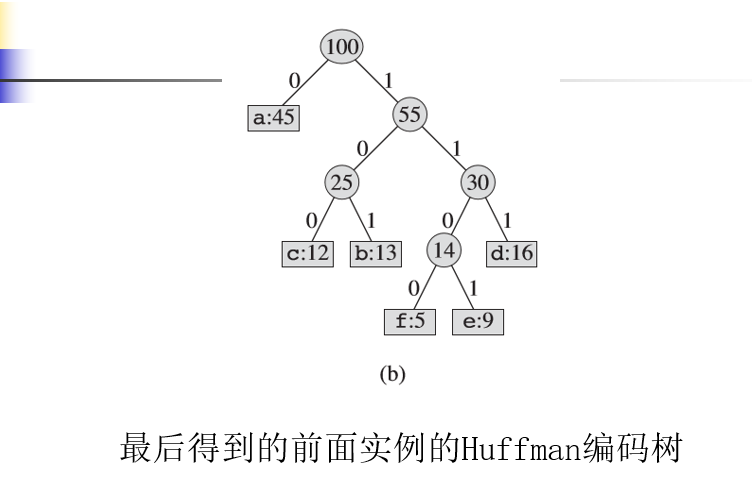
时间分析：假设\(Q\)使用小根堆，合并操作执行了\(n - 1\)次，每次合并操作需要取最小的两个子树，代价是\(logn\)，故总的复杂度是：\(O(nlogn)\)

注：如果将最小二叉堆换为van Emde Boas树，可以将运行时间减少到\(O(nloglogn)\)

HUFFMAN算法的正确性

引理 16.2: 令\(C\)为一个字母表，其中每个字符\(c\in C\)都有一个频率\(c.freq\)。令\(x\)和\(y\)是\(C\)中频率最低的两个字符。那么存在\(C\)的一个最优前缀码，\(x\)和\(y\)的码字长度相同，且只有最后一个二进制位不同。

证明：

令\(T\)是一个最优前缀码所对应的编码树——满二叉树。令\(a\)和\(b\)是\(T\)中深度最大的兄弟叶结点。

• 不是一般性，假设\(a.freq\leq b.freq\)且\(x.freq \leq y.freq\)。

• 由于\(x\)和\(y\)是叶结点中频率最低的两个结点，所以应有\(x.freq\leq a.freq\)且\(y.freq \leq b.freq\)。

• \(n\)若\(x.freq=b.freq\)，则有\(a.freq=b.freq=x.freq=y.freq\)，此时引理显然成立。

• 假定\(x.freq \neq b.freq\)，即\(x\neq b\)。则在T中交换\(x\)和\(a\)，生成一棵新树\(T’\)；然后再在\(T’\)中交换\(b\)和\(y\)，生成另一棵新树\(T''\)，那么在\(T''\)中\(x\)和\(y\)是深度最深的两个兄弟结点。如图所示：

  在最优树\(T\)中，叶子结点\(a\)和\(b\)是最深的叶子结点中的两个，并且是兄弟结点。叶子结点\(x\)和\(y\)为算法首先合并的两个叶子结点，它们可出现在\(T\)中的任意位置上。假设\(x\neq b\)，叶子结点\(a\)和\(x\)交换得到树\(T’\)，然后交换叶子结点\(b\)和\(y\)得到树\(T''\)。

• 根据文件编码的计算公式，\(T\)和\(T’\)的代价差为：

  \[B(T) - B(T')\\ = \sum_{c \in C} c.freq \times d_T(c) - \sum_{c \in C}c.freq \times d_{T'}(c)\\ =(x.freq \times d_T(x) + a.freq\times d_T(a) - x.freq \times d_{T'}(x) - a.freq\times d_{T'}(a)\\ = x.freq \times d_T(x) + a.freq\times d_T(a) - x.freq \times d_T(a) + a.freq\times d_T(x)\\ =(a.freq - x.freq)(d_T(a) - d_T(x)) \geq 0 \]

  \(B(T) - B(T') \geq 0\)表示从\(T\)到\(T'\)并没有增加代价

• 类似地，从\(T'\)到\(T''\)，交换\(y\)和\(b\)也不会增加代价，即\(B(T') - B(T'') \geq 0\)

  故\(B(T'') \leq B(T)\)

根据假设，\(T\)是最优的，因此\(B(T'')= B(T)\)，即得证：\(T''\)也是最优解，且\(x\)和\(y\)是其中深度最大的两个兄弟结点，\(x\)和\(y\)的码字长度相同，且只有最后一个二进制位不同。

得证引理16.2

下面不失一般性，通过合并来构造最优树。贪心选择：每次选择出现频率最低的两个字符。

• 将一次合并操作的代价视为被合并的两项的频率之和，而编码树构造的总代价等于所有合并操作的代价之和。

• 引理16.3表明：在所有的合并操作中，HUFFMAN选择是代价最小的方案：

引理 16.3 令\(C\)为一个给定的字母表，其中每个字符\(c\in C\)都有一个频率\(c.freq\)。

• 令\(x\)和\(y\)是\(C\)中频率最低的两个字符。

• 令\(C'\)为\(C\)去掉字符\(x\)和\(y\)，并加入一个新字符\(z\)后得到的字母表，即\(C'= C - \{x, y\}\cup \{z\}\)。

• 类似\(C\)，也为\(C'\)定义\(freq\)，且\(z.freq= x.freq + y.freq\)。

• 令\(T'\)为字母表\(C'\)的任意一个最优前缀码对应的编码树。

则有：可以将\(T'\)中叶子结点z替换为一个以\(x\)和\(y\)为孩子的内部结点，得到树\(T\)，而\(T\)表示字母表\(C\)的一个最优前缀码。

证明：

对\(C\)中不是\(x\)和\(y\)的字符\(c\)，即\(c \in C - \{x , y\}\),有\(d_T(c) = d_{T'}(c)\),亦有\(c.freq \times d_T(c) = c.freq \times d_{T'}(c)\)

因为：\(d_T(x) = d_T(y) = d_{T'}(z) + 1\)

所以有：

\[x.freq \times d_T(x) + y.freq \times d_T(y)\\ = (x.freq + y.freq)(d_{T'}(z) + 1)\\ = z.freq \times d_{T'}(z) + (x.freq + y.freq) \]

从而可得\(B(T) = B(T') + x.freq + y.freq\)或等价地\(B(T') = B(T) - x.freq - y.freq\)

下面用反证法证明T对应的前缀码是\(C\)的最优前缀码：

假定\(T\)对应的前缀码不是\(C\)的最优前缀码。则会存在最优前缀码树\(T''\)满足：\(B(T'')<B(T)\)。不失一般性，由引理16.2有，\(T''\)包含兄弟结点\(x\)和\(y\)。令\(T'''\)为将\(T''\)中\(x、y\)及它们的父结点替换为叶结点\(z\)得到的树，其中\(z.freq=x.freq+y.freq\)。于是

\[B(T''') = B(T'') - x.freq - y.freq\\ < B(T) - x.freq - y.freq\\ = B(T') \]

这与\(T’\)对应\(C’\)的一个最优前缀码的假设矛盾。 因此，\(T\)必然表示字母表\(C\)的一个最优前缀码。 证毕

定理 16.4 过程HUFFMAN会生成一个最优前缀码。

证明：由引理16.2和引理16.3即可得。

贪心选择性：

• 引理16.2说明首次选择频率最低的两个字符和选择其它可能的字符一样，都可以构造相应的最优编码树。

• 引理16.3说明首次贪心选择，选择出频率最低的两个字符\(x\)和\(y\)，合并后将\(z\)加入元素集合，可以构造包含\(z\)的最优编码树，而还原\(x\)和\(y\)，一样还是最优编码树。

所以贪心选择性成立。