活动选择问题

问题描述：假定有一个活动的集合\(S\)含有\(n\)个活动\(\{a_1,a_2,…,a_n\}\)，每个活动\(a_i\)都有一个开始时间\(s_i\)和结束时间\(f_i\)，\(0\leq s_i< f_i < \infin\)。同时，这些活动都要使用同一资源(如演讲会场)，而这个资源在任何时刻只能供一个活动使用。活动的兼容性：如果选择了活动\(a_i\)，则它在半开时间区间\([s_i, f_i)\)内占用资源。若两个活动\(a_i\)和\(a_j\)满足\([s_i, f_i)\)与区间\([s_j, f_j)\)不重叠，则称它们是兼容的。

活动选择问题：就是对给定的包含\(n\)个活动的集合\(S\)，在已知每个活动开始时间和结束时间的条件下，从中选出最多可兼容活动的子集合，称为最大兼容活动集合。不是一般性，设活动已经按照结束时间单调递增排序：\(f_1\leq f_2 \leq ...\leq f_n\)

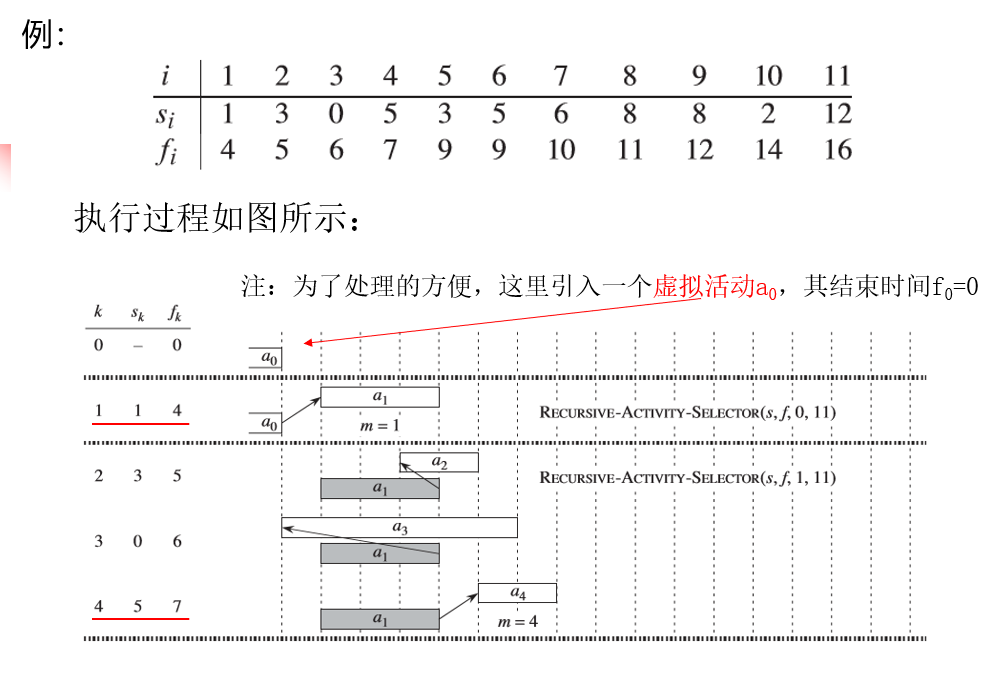
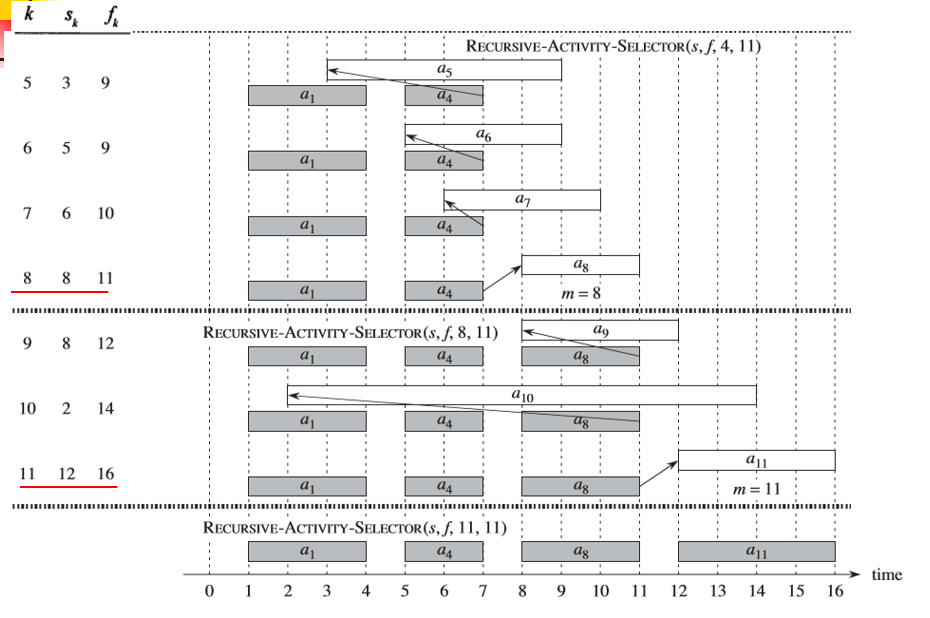
例：设有\(11\)个待安排的活动，它们的开始时间和结束时间如下，并设活动按结束时间的非递减次序排列：

\(i\)	1	2	3	4	5	6	7	8	9	10	11
\(s_i\)	1	3	0	5	3	5	6	8	8	2	12
\(f_i\)	4	5	6	7	9	9	10	11	12	14	16

则\(\{a_3 , a_9 , a_{11}\}\) 、\(\{a_1 , a_4 , a_8 , a_{11}\}\) 、 \(\{a_2 , a_4 , a_9 , a_{11}\}\)都是兼容活动集合。其中\(\{a_1 , a_4 , a_8 , a_{11}\}\) 、 \(\{a_2 , a_4 , a_9 , a_{11}\}\)是最大兼容活动的集合。显然最大兼容活动集合不一定是唯一的。

动态规划做法

活动选择问题的最优子结构

令\(S_{i , j}\)表示在\(a_i\)结束之后开始且在\(a_j\)开始之前结束的那些活动的集合。问题和子问题的形式定义如下：

设\(A_{i , j}\)是\(S_{i , j}\)的一个最大兼容活动集，并设\(A_{i , j}\)包含活动\(a_k\)，则有：\(A_{i , k}\)表示\(A_{i , j}\)中\(a_k\)开始之前的活动子集，\(A_{k,j}\)表示\(A_{i,j}\)中\(a_k\)结束之后的活动子集。并得到两个子问题：寻找\(S_{i , k}\)的最大兼容活动集合和寻找\(S_{k , j}\)的最大兼容活动集合。活动选择问题具有最优子结构性，也即：\(A_{i ,k}\)是\(S_{i , k}\)一个最大兼容活动子集，\(A_{k , j}\)是\(S_{k , j}\)的一个最大兼容活动子集。而\(A_{i ,j} = A_{i , k} \cup {a_k} \cup A_{k , j}\)。

证明：用剪切-粘贴法证明最优解\(A_{i , j}\)必然包含两个子问题\(S_{i,k}\)和\(S_{k,j}\)的最优解。

设\(S_{k,j}\)存在一个最大兼容活动集\(A_{k,j}’\)，满足\(|A_{k,j}’|>|A_{k,j}|\)，则可以将\(A_{k,j}’\)作为\(S_{i,j}\)最优解的一部分。这样就构造出一个兼容活动集合，其大小 \(|A_{i , k}|+|A_{k,j}’|+1> |A_{i , k}|+|A_{k,j}|+1=A_{i,j}\)与\(A_{i , j}\)是最优解相矛盾。得证。

令\(f(i , j)\)表示集合\(S_{i , j}\)的最优解的大小，则其转移方程为：

\[f(i , j) = f(i , k) + f(k , j) + 1 \]

为了选择\(k\)，则有：

\[f(i , j) = \begin{cases} 0 & s_{i , j} = \emptyset \\ \mathop{max}\limits_{a_k \in S_{i , j}} \{f(i , k) + f(k , j) + 1\} & s_{i , j} \neq \emptyset \end{cases} \]

贪心做法

贪心选择：在贪心算法的每一步所做的当前最优选择（局部最优选择）就叫做贪心选择。

活动选择问题的贪心选择：每次总选择具有最早结束时间的兼容活动加入到集合\(A\)中。该算法的贪心选择的意义是使剩余的可安排时间段最大化，以便安排尽可能多的兼容活动。

以上述例题为例，由于输入的活动已经按照结束时间的递增顺序排列好了，所以，首次选择的活动是\(a_1\)，其后选择的是结束时间最早且开始时间不早于前面已选择的最后一个活动的结束时间的活动 （活动要兼容）。

• 当输入的活动已按结束时间的递增顺序排列，贪心算法只需\(O(n)\)的时间即可选择出来\(n\)个活动的最大兼容活动集合。

• 如果所给出的活动未按非减序排列，可以用\(O(nlogn)\)的时间重排。

正确性证明：

定理16.1 考虑任意非空子问题\(S_k\)，令\(a_m\)是\(S_k\)中结束时间最早的活动，则\(a_m\)必在\(S_k\)的某个最大兼容活动子集中。

证明：

令\(A_k\)是\(S_k\)的一个最大兼容活动子集，且\(a_j\)是\(A_k\)中结束最早的活动。若\(a_j=a_m\)，则得证。

否则，令 \(A_k’=A_k-\{a_j\}\cup \{a_m\}\)。因为\(A_k\)中的活动都是不相交的，\(a_j\)是\(A_k\)中结束时间最早的活动，而\(a_m\)是\(S_k\)中结束时间最早的活动，所以\(f_m≤f_j\)。即\(A_k’\)中的活动也是不相交的。由于\(|A_k’|=|A_k|\)，所以\(A_k’\)也就是\(S_k\)的一个最大兼容活动子集，且包含\(a_m\)。得证。

伪代码：

这里数组\(s、f\)分别表示\(n\)个活动的开始时间和结束时间,并假定\(n\)个活动已经按照结束时间单调递增排列好。对当前的\(k\)，算法返回\(S_k\)的一个最大兼容活动集。
执行示例：

630. 课程表 III

题目描述：这里有\(n\)门不同的在线课程，按从$ 1$ 到$ n$ 编号。给你一个数组 \(courses\) ，其中$ courses[i] = [duration_i, lastDay_i] \(表示第\) i \(门课将会 持续 上\) duration_i $天课，并且必须在不晚于 $lastDay_i \(的时候完成。你的学期从第\) 1 $天开始。且不能同时修读两门及两门以上的课程。返回你最多可以修读的课程数目。

数据范围：\(1 \leq courses.length \leq 10^4 , 1 \leq duration_i , lastDay_i \leq 10^4\)

思路一：使用动态规划求解，考虑先对原有课程信息按照截止时间从小到大排序，定义状态\(f_i\)表示到第\(i\)天能够修读的课程数目，易得其转移方程为：

\[f_i = max(f_i , f[i - duration_j] + 1) \; \forall 1 \leq j \leq courses.length , duration_j \leq i \leq lastDay_j \]

时间复杂度：\(O(nlogn + n^2)\)

参考代码：

class Solution {
    public int scheduleCourse(int[][] courses) {
        final int N = 10005;
        int[] f = new int[N];
        int res = 0;
        Arrays.sort(courses , (a , b)->{
            if(a[1] != b[1]) return a[1] - b[1];
            return a[0] - b[0];
        });
        for(int[] course : courses){
            int k = course[0] , n = course[1];
            for(int i = n ; i >= k ; --i) f[i] = Math.max(f[i] , f[i - k] + 1);
        }
        for(int i = 1 ; i < N ; ++i) res = Math.max(res , f[i]);
        return res;
    }
}

思路二：使用贪心求解，还是先对原有课程信息按照截止时间从小到大排序。假设\(S\)为排序好后的前\(i\)个课程中能选择的最大数量所对应的需要的时间-\(duration\)，并设修读完这些课程的总时间为\(total\)，对于第\(i + 1\)个课程，假设需要时间为\(t\)，截止时间为\(k\)，如果\(total + t \leq n\)，那么直接将该门课程放入集合\(S\)中即可，并更新\(total\)为\(total + t\)；否则，如果\(S \neq \emptyset\)，且\(S\)中的最大的\(duration > t\)，那么就将该最大值移除集合\(S\)，并将第\(i + 1\)个课程需要的时间放入集合\(S\)中，最终的答案为\(|S|\)。显然集合\(S\)可以使用\(heap\)或者\(multiset\)进行维护。
时间复杂度：\(O(nlogn)\)
参考代码：

class Solution {
    public int scheduleCourse(int[][] courses) {
        PriorityQueue<Integer> heap = new PriorityQueue<>((a , b)->{
            return b - a;
        });
        Arrays.sort(courses , (a , b)->{
            if(a[1] != b[1]) return a[1] - b[1];
            return a[0] - b[0];
        });
        int total = 0;
        for(int[] course : courses){
            int k = course[0] , n = course[1];
            if(total + k <= n){
                heap.add(k);
                total += k;
            }
            else if(!heap.isEmpty() && heap.peek() > k){
                total -= heap.poll() - k;
                heap.add(k);
            }
        }
        return heap.size();
    }
}