最优二叉搜索树

• 背景：语言翻译，从英语到法语，对于给定的单词在单词表里找到该词
• 方法：创建一棵二叉搜索树，以英语单词作为关键字构建树
• 目标：尽快地找到英语单词，使总的搜索时间尽量少
• 思路：频繁使用的单词，如the应尽可能的靠近根；而不经常出现的单词可以离根远一点

前提假设：所有元素互异

一些定义：

• 二叉搜索树

  二叉搜索树\(T\)是一棵二元树，它或者为空，或者其每个结点含有一个可以比较大小的数据元素，且有：

  • \(T\)的左子树的所有元素比根结点中的元素小；
  • \(T\)的右子树的所有元素比根结点中的元素大；
  • \(T\)的左子树和右子树也是二叉搜索树。

• 最优二叉搜索树

  给定含有\(n\)个关键字的已排序的序列\(K=<k_1,k_2,…,k_n>\)（不失一般性，设 \(k_1<k_2<…<k_n\)），对每个关键字\(k_i\)，都有一个概率\(p_i\)表示其被搜索的频率。根据\(k_i\)和\(p_i\)构建一个二叉搜索树\(T\)，每个\(k_i\)对应树中的一个结点。

  搜索对象\(x\)，在\(T\)中可能找到、也可能找不到：

  • 若\(x\)等于某个\(k_i\)，则一定可以在\(T\)中找到结点\(k_i\)，称为成功搜索。成功搜索的情况一共有\(n\)种，分别是\(x\)恰好等于某个\(k_i\)。
  • 若\(x<k_1\) 或$ x>k_n$ 或\(k_i<x<k_{i+1} (1\leq i<n)\), 则在\(T\)中搜索\(x\)将失败，称为失败搜索。
    • 为此引入外部结点\(d_0,d_1,...,d_n\)，用来表示不在\(K\)中的值,称为伪关键字。
    • 伪关键字在\(T\)中对应外部结点,共有\(n+1\)个。—扩展二叉树：内结点表示关键字\(k_i\)，外结点(叶子结点)表示\(d_i\)
    • 这里每个\(d_i\)代表一个区间。\(d_0\)表示所有小于\(k_1\)的值， \(d_n\)表示所有大于\(k_n\)的值，对于\(i=1,…,n-1\)，\(d_i\)表示所有在\(k_i\)和\(k_{i+1}\)之间的值。每个\(d_i\)也有一个概率表示搜索对象x恰好落\(q_i\)入区间\(d_i\)的频率。

• 二叉搜索树的期望搜索代价

  • 一次搜索的代价等于从根结点开始访问结点的数量（包括外部结点）。从根结点开始访问结点的数量等于结点在\(T\)中的深度\(+ 1\)。记\(depth_T(i)\)为结点\(i\)在\(T\)中的深度。

  • 二叉搜索树\(T\)的期望代价为：

    \[E[search\;cost\;in\;T] = \sum_{i = 1}^{n} (depth_T(k_i) + 1) * p_i + \sum_{i = 0}^{n}(depth_T(d_i) + 1) * q_i\\ = 1 + \sum_{i = 1}^ndepth_T(k_i)*p_i + \sum_{i = 0}^n depth_T(d_i) * q_i \]

• 最优二叉搜索树

  对于给定的关键字及其概率集合，期望搜索代价最小的二叉搜索树称为其最优二叉搜索树。

  关键问题在于确定谁是根：1.树根不一定是概率最高的关键字；2.树也不一定是最矮的树；3.该树的期望搜索代价必须是最小的。

证明最优二叉搜索树的最优子结构：

如果\(T\)是一棵相对于关键字\(k_1,…,k_n\)和伪关键字\(d_0, …,d_n\)的最优二叉搜索树，则\(T\)中一棵包含关键字\(k_i,…,k_j\)的子树\(T'\)必然是相对于关键字\(k_i,…,k_j\)（和伪关键字\(d_{i-1}, …,d_j\)）的最优二叉搜索子树。

证明：用剪切-粘贴法证明

对关键字\(k_i,…,k_j\)和伪关键字\(d_{i-1},…,d_j\)，如果存在子树\(T''\)，其期望搜索代价比\(T'\)低，那么将\(T'\)从\(T\)中删除，将\(T''\)粘贴到相应位置上，则可以得到一棵比\(T\)期望搜索代价更低的二叉搜索树，与\(T\)是最优的假设矛盾。

构造最优二叉搜索树

利用最优二叉搜索树的最优子结构性来构造最优二叉搜索树。

分析： 对给定的关键字\(k_i,…,k_j\)，若其最优二叉搜索（子）树的根结点是\(k_r（i\leq r \leq j）\)，则\(k_r\)的左子树中包含关键字\(k_i,…,k_{r-1}\)及伪关键字\(d_{i-1} , …,d_{r-1}\)，右子树中将含关键字\(k_{i+1},…,k_j\)及伪关键字\(d_r,…,d_j\)。

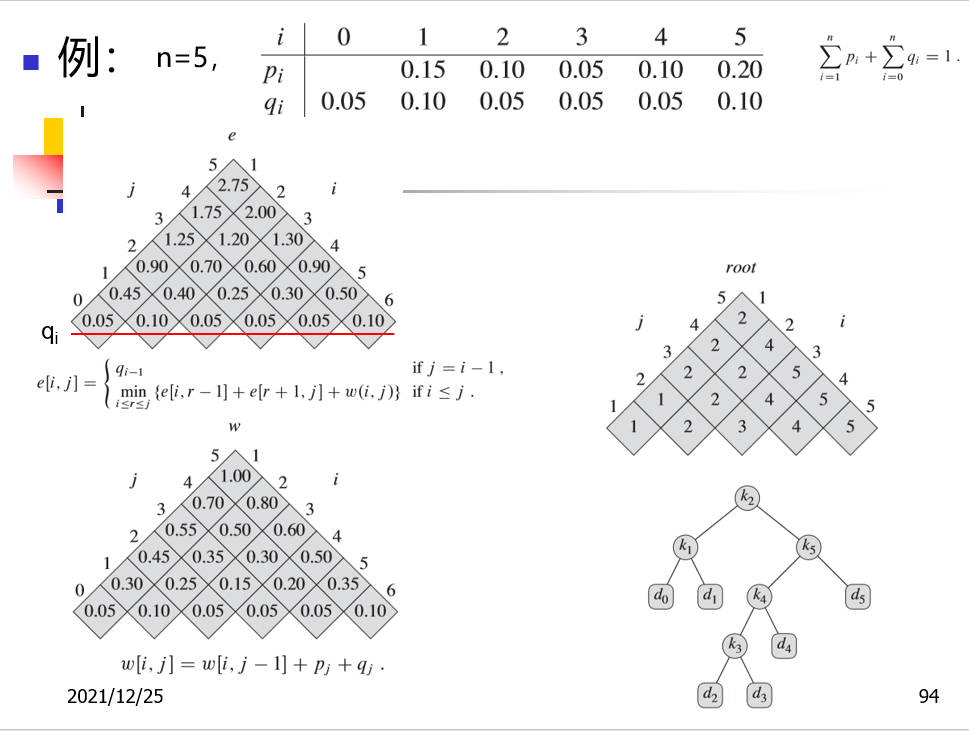
计算过程：求解包含关键字\(k_i,...,k_j\)的最优二叉搜索树，其中\(i \geq 1 , j \leq n , j \geq i - 1\)。定义\(e[i , j]\)表示包含关键字\(k_i , ...,k_j\)的最优二叉搜索树的期望搜索代价，最终解的期望搜索代价为\(e[1 , n]\)。

1. 当\(i \leq j\)时，从\(k_i , ..., k_j\)中选择出根结点\(k_r\)。其左子树包含关键字\(k_i , ... , k_{r - 1}\)且是最优二叉搜索子树；其右子树包含关键字\(k_{r + 1} , ... , k_j\)且同样为最优二叉搜索树。

2. 当一棵树成为另一个结点的子树时，有以下变化：子树的每个结点的深度增加\(1\)，根据搜索代价期望值计算公式，子树对根为\(k_r\)的树的期望搜索代价的贡献是其期望搜索代价+其所含有结点的概率之和。对于包含关键字\(k_i , ... , k_j\)的子树，所有结点的概率之和为（包含外部结点）：\(\omega(i ,j) = \sum_{l = i}^j p_l + \sum_{l= i - 1}^j q_l\) 。

3. 若\(k_r\)为包含关键字\(k_i , ...,k_j\)的最优二叉搜索树的根，则其期望搜索代价\(e[i , j]\)与左右子树的期望搜索代价\(e[i , r - 1]\)和\(e[r + 1 , j]\)的递推关系式为：

   \[e[i , j] = p_r + (e[i , r - 1] + \omega(i , r - 1)) + (e[r + 1 , j] + w(r + 1 , j)) \]

   其中\(\omega(i , r - 1)\)和\(\omega(r + 1 , j)\)是左右子树所有结点的概率之和。且有\(\omega(i , j) = \omega(i , r - 1) + p_r + \omega(r + 1 , j)\)

   故递推关系式等价于：\(e[i , j] = e[i , r - 1] + e[r + 1 , j] + w(i , j)\)

   总的递推关系式为：

   \[e[i , j] = \begin{cases} q_{i - 1} & j = i - 1\\ \mathop{min}\limits_{i \leq r \leq j} \{e[i , r - 1] + e[r + 1 , j] + w(i , j)\} & i \leq j \end{cases} \]

4. 边界条件

   上述递推关系式存在\(e[i , i - 1]\)和\(e[j + 1 , j]\)的边界情况。此时子树不包含实际的关键字，而只包含伪关键字\(d_{i - 1}\)，其期望搜索代价仅为\(e[i , i - 1] = q_{i - 1}\)

5. 构造最优二叉搜索树

   定义\(root[i , j]\)，保存计算\(e[i , j]\)时，使\(e[i, j]\)取得最小值的\(r\)，\(k_r\)即为关键字\(k_i,…,k_j\)的最优二叉搜索（子）树的树根。在求出\(e[1,n]\)后，利用\(root\)即可构造出最终的最优二叉搜索树。

计算最优二叉搜索树的期望值

定义三个数组：

• \(e[1...n + 1 , 0...n]\):用于记录所有\(e[i , j]\)的值，其中\(e[n + 1 , n]\)表示伪关键字\(d_n\)对应的子树；\(e[1 , 0]\)表示伪关键字\(d_0\)对应的子树
• \(root[1...n]\)：用于记录所有最优二叉搜索子树的根节点
• \(\omega[1...n + 1 , 0...n]\)：用于保存子树的结点的概率之和，且有\(\omega(i , j) = \omega(i , j - 1) + p_j + q _j\),这样每个\(\omega(i , j)\)的计算时间仅为\(\Theta(1)\)。

伪代码：

时间复杂度：\(O(n^3)\)
空间复杂度：\(O(n^2)\)
一个简单的示例: