算法复习

以下内容和相关链接内的内容大多摘抄自王多强老师的PPT

循环不变式：把在第一次进入循环之前成立、以后每次循环之后还成立的关系称为‘循环不变关系“或’循环不变式‘、’循环不变性质

利用循环不变关系证明循环的正确性

分三步：

• 初始化：证明初始状态时循环不变式成立，即证明循环不变式在循环开始之前为真
• 保持：证明每次循环之后、下一次循环开始之前循环不变式仍为真
• 终止：证明循环可以在有限次循环后终止

为什么更关心算法的最坏情况执行时间

• 一个算法的最坏情况执行时间给出了任何输入的运行时间的一个上界。知道了这个上界，就能确保算法绝对不需要更长的时间
• 对于某些算法，最坏情况经常出现
• 对于很多算法，平均情况往往与最坏情况大致一样

限界函数：取自频率计算函数表达式中的最高次项，并忽略常系数，记为；\(g(n)\)

• \(g(n)\)是关于\(n\)的形式简单的单项式函数，如\(logn\) ，\(nlogn\)
• \(g(n)\)是对算法中最复杂的计算部分分析而来的

算法的五个重要特性

• 确定性：算法使用的每种运算必须要有确切的定义，不能存在二义性
• 能行性：算法中有待实现的运算都是基本的运算，原理上每种运算都能由人用纸和笔在“有限”的时间内完成
• 输入：每个算法都有0个或多个输入
• 输出：一个算法产生一个或多个输出，这些输出是同输入有某种特定关系的量
• 有穷性：一个算法总是在执行了有穷步的运算之后终止

限界函数的定义

记算法的实际执行时间为\(f(n)\) ， 分析所得到的限界函数为\(g(n)\)

• 上界函数\(O\)

  \(O(g(n))\)表示以下函数的集合

  \[f(n) \; :\; there\;exist\;positive\;constants\;c\;and\;n_0\;such \;that\; 0 \leq f(n) \leq cg(n) \forall n \geq n_0 \]

  若\(f(n)\)和\(g(n)\)满足以上关系，则记为\(f(n) \in O(g(n))\)，表示\(f(n)\)是集合\(O(g(n))\)的成员，并通常记作\(f(n) = O(g(n))\) ，其意义可解释为：如果算法用\(n\)值不变的同一类数据在某台机器上运行，所用的时间总小于\(|g(n)|\)的一个常数倍

  上界函数代表了算法最坏情况下的时间复杂度

  在确定上界函数时，应当找阶最小的\(g(n)\)作为\(f(n)\)的上界函数-紧确上界

  如：\(3n + 2 = O(n^2)\) 是松散的界限而\(3n + 2 = O(n)\)是紧确的界限

• 下界函数\(\Omega\)

  \(\Omega(g(n))\)表示以下函数的集合

  \[f(n) \; :\; there\;exist\;positive\;constants\;c\;and\;n_0\;such \;that\; 0 \leq cg(n) \leq f(n) \forall n \geq n_0 \]

  若\(f(n)\)和\(g(n)\)满足以上关系，则记为\(f(n) \in \Omega(g(n))\)，表示\(f(n)\)是集合\(\Omega(g(n))\)的成员，并通常记作\(f(n) = \Omega(g(n))\) ，其意义可解释为：如果算法用\(n\)值不变的同一类数据在某台机器上运行，所用的时间总不小于\(|g(n)|\)的一个常数倍

  在确定下界函数时，应当找阶最大的\(g(n)\)作为\(f(n)\)的下界函数-紧确下界

  如：\(3n^2 + 2 = O(n)\) 是松散的界限 而\(3n^2 + 2 = O(n^2)\)是紧确的界限

• 渐进紧确界函数\(\Theta\)

  \(\Theta(g(n))\)表示以下函数的集合

  \[f(n) \; :\; there\;exist\;positive\;constants\;c_1 , c_2\;and\;n_0\;such \;that\; 0 \leq c_1g(n) \leq f(n) \leq c_2g(n) \forall n \geq n_0 \]

  若\(f(n)\)和\(g(n)\)满足以上关系，则记为\(f(n) \in \Theta(g(n))\)，表示\(f(n)\)是集合\(\Theta(g(n))\)的成员，并通常记作\(f(n) = \Theta(g(n))\) ，其意义可解释为：如果算法用\(n\)值不变的同一类数据在某台机器上运行，所用的时间既不小于\(|g(n)|\)的一个常数倍，也不大于\(|g(n)|\)的一个常数倍，也即\(g(n)\)既是\(f(n)\)的下界，也是上界
  \(\Theta\)记号给出的是渐进紧确界，从时间复杂度的角度看，\(f(n) = \Theta(g(n))\)表示是算法在最好和最坏情况下的计算时间就一个常数因子范围内而言是相同的，可以看作：既有\(f(n)= \Omega(g(n))\)，又有\(f(n) = O(g(n))\)。

\(o\)记号：对于任意的正常数\(c\)，存在常数\(n_0 > 0\) , 使对所有的\(n \geq n_0\) ，有\(|f(n)| \leq c|g(n)|\),则记作：\(f(n) = o(g(n))\)

含义：在\(o\)表示中，当\(n\)趋于无穷时，\(f(n)\)相对于\(g(n)\)来说变得微不足道了，即\(\lim_{n \to \infin}\frac{f(n)}{g(n)} = 0\)

例如：\(2n = o(n^2)\) ， 但\(2n \neq o(n) 、 2n^2 \neq o(n^2)\)

\(\omega\)记号：对于任意的正常数\(c\)，存在常数\(n_0 > 0\) , 使对所有的\(n \geq n_0\) ，有\(c|g(n)| \leq |f(n)|\),则记作：\(f(n) = \omega(g(n))\)

含义：在\(\omega\)表示中，当\(n\)趋于无穷时，\(f(n)\)相对于\(g(n)\)来说变得任意大了，即\(\lim_{n \to \infin}\frac{f(n)}{g(n)} = \infin\)

例如：\(2n = \omega(n^2)\) ， 但\(\frac{n}{2} \neq \omega(n) 、 \frac{n^2}{2} \neq \omega(n^2)\)

限界函数的性质：

• 传递性
• 自反性 \(f(n) = \Theta(f(n))\)
• 对称性 \(f(n) = \Theta(g(n)) \;if\;and\;only\;if\;g(n) = \Theta(f(n))\)
• 转置对称性

相关定理

• 多项式定理：若\(A(n) = a_mn^m + ... + a_1n + a_0\)是一个关于\(n\)的\(m\)次多项式，则有\(A(n) = O(n^m)\)，即：变量\(n\)的固定阶数为\(m\)的多项式，与此多项式的最高阶\(n^m\)同阶

• 对于任意正实数\(x\)和\(\epsilon\) ，有下面的不等式

  • 存在某个\(n_0\) ,使得对于任何\(n \geq n_0\),有\((log n)^x < (log n)^{x+ε}\)

  • 存在某个\(n_0\) ,使得对于任何\(n \geq n_0\)，有\(n^x < n^{x+ε}\) 。

  • 存在某个\(n_0\) ,使得对于任何\(n \geq n_0\)，有\((log n)^x < n\)。

  • 存在某个\(n_0\) ,使得对于任何\(n \geq n_0\)，有\(n^x < 2^n\)。

  • 对任意实数\(y\),存在某个\(n_0\)，使得对于任何\(n \geq n_0\)， 有 $ n^x(log n)^y < n^{x+ε}$

分治法的基本思想：当问题规模比较大而无法直接求解时，将原问题分解为几个规模较小、但类似于原始问题的子问题，然后递归地求解这些子问题，最后合并子问题的解以后得到原始问题的解。

求解分治问题的步骤：

• 分解：将原问题分解为若干规模较小的、相互独立、形式与原问题一样的子问题
• 解决：若子问题规模较小、可直接求解时则直接求解，否则继续分解
• 合并：将子问题的解合并成原问题的解

典型问题：求解最大子数组（当然可以动态规划求解） 如果使用线段树可以求解支持单点修改的区间最大子数组 最大子数组问题

如何化简递归式得到形式简单的限界函数

• 代换法

  • 猜测解的形式
  • 用数学归纳法证明猜测的正确性

  例如：

  \[T(n) = 2T(\lfloor \frac{n}{2}\rfloor) + n \]

  猜测其解为\(T(n) = O(nlogn)\)

  代入法要证明的是：如何恰当选择常数\(c\)，使得\(T(n) \leq cnlogn\)成立

  假设该界对\(\lfloor\frac{n}{2}\rfloor\)成立，即\(T(\lfloor\frac{n}{2} \rfloor) \leq c\lfloor\frac{n}{2} \rfloor long(\lfloor\frac{n}{2} \rfloor)\)

  则在数学归纳法推论证明阶段对递归式做代换，有：

  \[T(n) \leq 2(c\lfloor\frac{n}{2} \rfloor log(\lfloor\frac{n}{2} \rfloor)) + n\\ \leq cnlog(\frac{n}{2}) + n\\ = cnlogn - cnlog2 + n\\ = cnlogn - (c - 1)n \]

  故要使\(T(n) \leq cnlogn\)成立，只需要\(c \geq 1\)即可，但这里需要检验边界是否满足然后调整\(c\)的值

• 递归树法

  根据递归式的定义，可以画一棵递归树

  递归树：反应递归的执行过程，每个节点表示一个单一子问题的代价，子问题对应某次递归调用。根节点代表顶层调用的代价，子节点分别代表各层递归调用的代价。

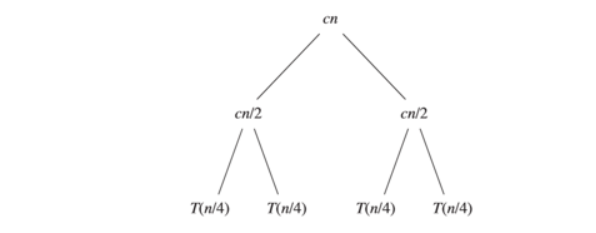
  \[T(n) = \begin{cases} c & if\; n = 1\\ 2T(\frac{n}{2}) + cn & if \;n > 1 \end{cases} \]

  

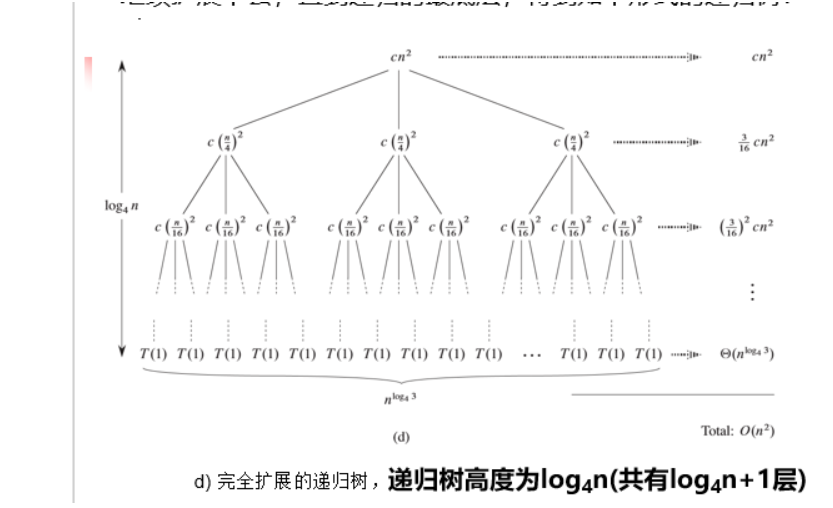
  例如求解:\(T(n) = 3T(\lfloor\frac{n}{4} \rfloor) + \Theta(n^2)\)

  准备工作后变为求解\(T(n) = 3T(\frac{n}{4}) + cn^2\)

  

  整棵树的总代价等于各层代价之和，则有

  \[T(n) = cn^2 + \frac{3}{16}cn^2 + ... + \Theta(n^{log_43})\\ = \sum_{i = 0}^{log_4n - 1} (\frac{3}{16})^icn^2 + \Theta(n^{log_43})\\ = \frac{\frac{3}{16}^{log_4n} - 1}{\frac{3}{16} - 1}cn^2 + \Theta(n^{log_43}) \]

• 主方法

  如果递归式有如下形式，在满足一定的条件下，可以用主方法直接给出渐近界：\(T(n) = aT(\frac{n}{b}) + f(n)\) .其中\(a , b\)是常数，且\(a \geq 1 , b\geq1\)；\(f(n)\)是一个渐近正的函数

  则\(T(n)\)可能有如下的渐近界:

  • 若对于某常数\(\epsilon > 0\) ， 则有\(f(n) = O(n^{log_ba - \epsilon})\) , 则\(T(n) = \Theta(n^{log_ba})\)
  • 若\(f(n) = \Theta(n^{log_ba})\)，则\(T(n) = \Theta(n^{log_ba}logn)\)
  • 若对某常数\(\epsilon > 0\)，有\(f(n) = \Omega(n^{log_ba + \epsilon})\)，且对常数\(c < 1\)与所有足够大的\(n\)，有\(af(\frac{n}{b}) \leq cf(n)\) ， 则\(T(n) = \Theta(f(n))\)

  若递归式中的\(f(n)\)与\(n^{log_ba}\)的关系不满足以下性质：

  • \(f(n) \leq n^{log_ba}\)，但不是多项式地小于
  • \(f(n) \geq n^{log_ba}\)，但不是多项式的大于

  则不能使用主方法求解该递归式

  使用主定理时不用再证明其正确性

平面最近点对问题->分治法求解 平面最近点对

动态规划

最优化问题：这一类问题的可行解可能有很多个。每个解都有一个值，我们希望寻找具有最优值的解（最小值或最大值）。

动态规划算法的步骤

• 刻画一个最优解的结构特征
• 递归地定义最优解的值
• 计算最优解的值
• 利用计算的信息，构造一个最优解

1. 前三步是动态规划算法求解问题的基础。如果仅需要一个最优解的值而非解本身，可以忽略步骤4
2. 如果确实要做步骤4，则需要在执行步骤3的过程中维护一些额外的信息
3. 第三步通常采用自底向上的方法计算最优解

钢条切割问题->完全背包 钢条切割问题

子问题图

当思考一个动态规划问题时，应该弄清楚所涉及的子问题与子问题之间的依赖关系，可以用子问题图描述：

子问题图：用于描述子问题与子问题之间的依赖关系

• 子问题图是一个有向图，每个顶点唯一地对应一个子问题
• 若求子问题\(x\)的最优解时需要直接用到子问题\(y\)的最优解，则在子问题图中就会有一条从子问题\(x\)的顶点到子问题\(y\)的顶点的有向边。

子问题图是自顶向下递归调用树的简化版

自底向上的动态规划方法处理子问题图中顶点的顺序为： 对一个给定的子问题\(x\)，在求解它之前先求解邻接至它的子问题。即对于任何子问题，仅当它依赖的所有子问题都求解完成了，才会求解它。 —— 逆拓扑序，深度优先原则进行处理。

基于子问题图“估算”算法的运行时间：算法的运行时间等于所有子问题求解的时间之和。子问题图中，子问题对应顶点，子问题的数目等于顶点数。一个子问题的求解时间与子问题图中对应顶点的“出度”成正比。 因此，一般情况下，动态规划算法的运行时间与顶点和边的数量至少呈线性关系。

矩阵链乘法 -> 矩阵链乘法

利用动态规划求解问题的方法：

• 证明问题满足最优性原理

  所谓“问题满足最优性原理”即：问题的最优决策序列具有最优子结构性。证明问题满足最优性原理是实施动态规划的必要条件：如果证明了问题满足最优性原理，则说明用动态规划方法有可能解决该问题。

• 获得问题状态的递推关系式

  能否求得各阶段间状态变换的递推关系式是解决问题的关键。

  \(f(x_1,x_2,…,x_i) →x_{i+1}\)向后递推或\(f(x_i,x_{i+1},…,x_n)→x_{i-1}\) 向前递推

动态规划实质上是一种以空间换时间的技术，它在实现的过程中，需要存储过程中产生的各种状态（中间结果），所以它的空间复杂度要大于其它的算法。

子问题无关性

子问题无关是指同一个原问题的一个子问题的解不影响另一个子问题的解，可以各自独立求解。

• 最长简单路径问题

  子问题间相关，不能使用动态规划策略求解

• 最短路径问题

  子问题不相关，满足最优子结构性，可以用动态规划问题求解

如何证明问题的最优解满足最优子结构性？

即证明：作为构成原问题最优解的组成部分，对应每个子问题的部分应是该子问题的最优解

剪切-粘贴技术：

​ 本质上是反证法：假定原问题最优解中对应的某个子问题的部分解不是该子问题的最优解，而存在“更优的子解”，那么我们可以从原问题的解中剪切掉这部分，而将更优的子解粘贴进去，从而得到一个比最优解更优的解，这与最初的解是原问题的最优解的前提假设相矛盾。因此不可能存在更优的子解。所以，原问题的子问题的解必须是其最优解，最优子结构性成立。

最长公共子序列问题 最长公共子序列问题
最优二叉搜索树 最优二叉搜索树

贪心

什么是贪心算法：分步骤实施，它在每一步仅作出当时看起来最佳的选择，即局部最优的选择，并寄希望这样的选择最终能导致全局最优解。

经典问题：最小生成树问题的Prim算法、Kruskal算法，单源最短路径Dijkstra算法等

活动选择问题 活动选择问题

贪心求解的一般步骤：

• 确定问题的最优子结构
• 将最优化问题转化为：每次对其作出选择后，只剩下一个子问题需要求解；
• 证明作出贪心选择后，剩余的子问题满足：其最优子解与前面的贪心选择组合即可得到原问题的最优解(具有最优子结构)。

注：对应每个贪心算法，都有一个动态规划算法，但动态规划算法要繁琐的多。

如何证明一个最优化问题适合用贪心算法求解

如果能够证明问题具有贪心选择性质和最优子结构性，则基本上就可以实施贪心策略

• 贪心选择性质

  可以通过做出局部最优选择来构造全局最优解的性质。贪心选择性使得我们进行选择时，只需做出当前看起来最优的选择，而不用考虑子问题的解。

• 最优子结构性

  见前文

Huffman编码 Huffman编码

部分背包问题->物体可切割 参考习题：部分背包

图论

宽度优先搜索

深度优先搜索

没啥好说的有空再补吧，反正很简单

分支-限界法：采用宽度优先策略，在生成当前\(E\)结点全部儿子之后再生成其它活结点的儿子，且用限界函数帮助避免生成不包含答案结点子树的状态空间的检索方法。

活结点表：

• 活结点：自己已经被生成，但还没有被检测的结点。
• 存储结构：
  • 队列（First In First Out, BFS）
  • 栈（Last In First Out, D-Search）
• 分支-限界法的两种基本设计策略：
  • FIFO检索：活结点表采用队列
  • LIFO检索：活结点表采用栈

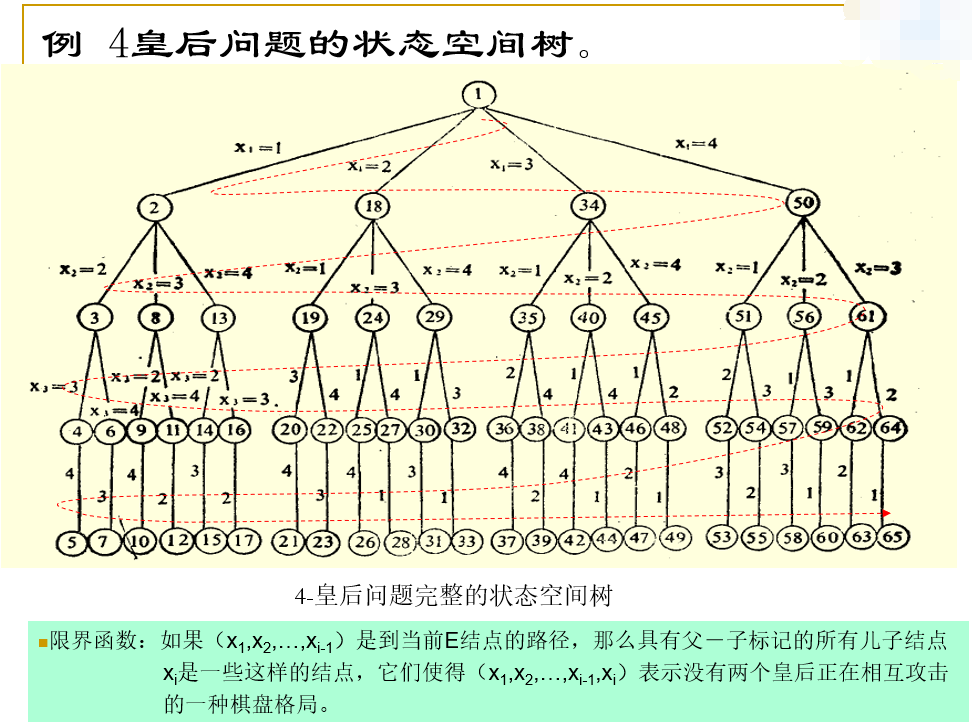
举例：\(4\)皇后问题的状态空间树以及其限界函数

LC-检索（\(A^{*}\)算法）

LIFO和FIFO分支-限界法存在的问题：对下一个\(E\)结点的选择规则过于死板。对于有可能快速检索到一个答案结点的结点没有给出任何优先权。

解决方法：寻找一种“有智力”的排序函数\(C(·)\)， 用\(C(·)\)来选取下一个E结点，加快到达一答案结点的检索速度。对于任一结点，用该结点导致答案结点的成本（代价）来衡量该结点的优先级——成本越小越优先。

对任一结点\(X\)，可以用两种标准来衡量结点的代价：

• 在生成一个答案结点之前，子树\(X\)需要生成的结点数
• 在子树\(X\)中离\(X\)最近的那个答案结点到\(X\)的路径长度。

\(C(·)\)：“有智力”的排序函数，依据成本排序，优先选择成本最小的活结点作为下一个E结点进行扩展。\(C(·)\)又称为“结点成本函数”

结点成本函数\(C(x)\)的取值：

• 如果\(X\)是答案结点，则\(C(X)\)是由状态空间树的根结点到\(X\)的成本(即所用的代价，可以是级数、计算复杂度等)。
• 如果\(X\)不是答案结点且子树\(X\)不包含任何答案结点，则 \(C(X)＝\infin\)
• 如果\(X\)不是答案结点但子树\(X\)包含答案结点，则\(C(X)\)应等于子树\(X\)中具有最小成本的答案结点的成本

计算结点成本函数的困难:计算结点\(X\)的代价通常要检索子树\(X\)才能确定，因此计算\(C(X)\)的工作量和复杂度与解原始问题是相同的。

为了解决上述问题，引入成本的估计函数\(\widehat{c}(X)\) 包括\(\widehat{g}(X)\)和\(h(X)\)

\(\widehat{g}(X)\)是由\(X\)到达一个答案结点所需成本的估计函数，但单纯使用它选择\(E\)结点会导致算法偏向纵深检查。故需引入\(h(X)\)（根结点到结点\(X\)的成本-已发生成本）改进成本估计函数。

改进后的结点成本估计函数\(\widehat{c}(X) = f(h(X)) + \widehat{g}(X)\)

\(f( \cdot )\)是一个非降函数。非零的\(f\)可以减少算法作偏向纵深检查的可能性，它强使算法优先检索更靠近答案结点但又离根较近的结点。

LC-检索：选择\(\widehat{c}(\cdot)\) 值最小的活结点作为下一个\(E\)结点的状态空间树检索方法。

特例：

• BFS：依据级数来生成结点，令\(\widehat{g}(X) = 0 , f(h(X)) = X\)的级数
• D-Search： 令\(f(h(x)) = 0\),而当\(Y\)是\(X\)的一个儿子时，总有\(\widehat{g}(X) \geq \widehat{g}(Y)\)

当有多个答案结点时，LC是否一定找得到具有最小成本的答案结点呢？否

不同估算函数对于结果的影响

• 当估算的距离\(\widehat{g}\)完全等于实际距离时，也就是每次扩展的那个点都准确的知道选它以后，路径距离是多少，这样就不用乱选了，每次都选最小的那个，一路下去，肯定就是最优的解，而且基本不用扩展其它的点。
• 如果估算距离\(\widehat{g}\)小于实际距离时，则到最后一定能找到一条最短路径，但是有可能会经过很多无效的点。
• 如果估算距离\(\widehat{g}\)大于实际距离时，有可能就很快找到一条通往目的地的路径，但是却不一定是最优的解。

最小成本的上界

定义\(U\)为最小成本解的成本上界，则：

作用：对具有\(\widehat{c}(X) > U\)的所有活结点可以被杀死，从而可以进一步使算法加速，减少求解的盲目性。根据\(c(X)\)的定义，由那些\(\widehat{c}(X) > U\)的结点\(X\)可到达的所有答案结点必有\(c(x) \geq \widehat{c}(X) \geq U\)，不可能具有更小的成本。故当已经求得一个具有成本\(U\)的答案结点，那些有\(\widehat{c}(X) > U\)的所有活结点都可以被杀死。

最小成本上界\(U\)的求取：

• 初始值：利用启发性方法赋初值，或置为\(\infin\)。只要\(U\)的初始值不小于最小成本答案结点的成本，利用\(U\)就不会杀死可以到达最小成本答案结点的活结点。
• 每找到一个新的答案结点后修正\(U\)，\(U\)取当前最小成本值。

N—皇后问题 - （待补，本质上也比较简单）

子集和数问题 子集和数问题 学会画那个状态空间树就行 具体实现比较简单

\(n\)数码问题 暴力搜索的复杂度为\(O(n!)\)，所以\(8\)数码是可以爆搜的，而\(16\)数码就需要使用\(A^*\)算法了，不要求

最小生成树

最小生成树 知道这俩算法咋执行的应该就差不多了

单源最短路

单源最短路径

多源最短路径

多源最短路

最大流

最大流问题