最大子数组问题
问题描述:给你一个长度为\(n\)的序列\(a\) , 选出其中连续且非空的一段使得这段和最大。即求
问题一
数据范围:
思路: 首先考虑暴力,显然可以枚举区间端点,然后对这个区间内的值求和,最终再取最大值即可,复杂度为:\(O(n^3)\),考虑优化最内层循环,即使用前缀和,可以\(O(1)\)求出子数组的和,此时时间复杂度为:\(O(n^2)\)。显然这样的复杂度依旧不可接受,考虑继续优化。考虑以第\(i\)个数结尾的最大子段和为\(f_i\),其显然只与子数组\(a[1...i-1]\)的后缀的最大值以及自身的值有关,而子数组\(a[1...i - 1]\)以第\(i - 1\)个数结尾的最大字段和为\(f_{i - 1}\),所以可以得出\(f_i\)的转移过程为\(f_i = max(a_i , f_{i - 1} + a_i)\).这样的复杂度为\(O(n)\),可以通过此题。当然可以分治求解复杂度\(O(nlogn)\),关于分治的合并过程请参考下文关于区间最大子段和问题。
参考代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int f[N], a, n, res;
void solve() {
f[0] = -N;
res = INT_MIN;
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a;
f[i] = max(a, f[i - 1] + a);
res = max(res, f[i]);
}
cout << res << '\n';
return;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T = 1;
while (T--) solve();
return 0;
}
问题二
题目描述:给定一个长度为\(n\)的整数序列,要求从中选出两个连续子序列,使得这两个连续子序列的序列和之和最大,最终只需输出最大和。一个连续子序列的和为该子序列中所有数之和。每个连续子序列的最小长度为\(1\),并且两个连续子序列之间至少间隔一个数。
数据范围: \(n \leq 10^6\) 保证答案不超过\(int64\)
思路:显然我们可以先从前往后和从后往前做一遍最大子段和,分别记作\(l\)和\(r\),然后我们分别对它们做前缀最大值和后缀最大值,接下来就是枚举分界点\(i\) , 然后更新答案即可,答案的更新过程为\(res = max(res , l[i - 1] + r[i + 1]) , 2\leq i \leq n - 1\)
时间复杂度:\(O(n)\)
参考代码:
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f3f3f3f
using ll = long long;
const int N = 1e6 + 5;
ll a[N], l[N], r[N], n, res;
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> a[i];
l[1] = a[1]; r[n] = a[n];
for (int i = 2; i <= n; ++i) l[i] = max(a[i], l[i - 1] + a[i]);
for (int i = 2; i <= n; ++i) l[i] = max(l[i], l[i - 1]);
for (int i = n - 1; i >= 1; --i) r[i] = max(a[i], r[i + 1] + a[i]);
for (int i = n - 1; i >= 1; --i) r[i] = max(r[i], r[i + 1]);
res = -INF;
for (int i = 2; i < n; ++i) res = max(res, l[i - 1] + r[i + 1]);
cout << res << endl;
return 0;
}
问题三
题目描述:给出一段长度为 \(n\)的环状序列 \(a\),即认为 \(a_1\) 和 \(a_n\) 是相邻的,选出其中连续不重叠且非空的两段使得这两段和最大。
数据范围:\(2 \leq n \leq 2 \times 10^5 , -10^4 \leq a_i \leq 10^4\)
思路:对于环状问题,我们需要将环拆开来看,首先比较显然的是问题的答案有两种形式:
其中\(0\)表示不选,\(1\)表示选
那么对于第一种情况,就是问题二,直接使用第二题的代码即可;对于第二种情况j就是整个数组的\(sum\)减去两段不要的,把\(max\)换成\(min\)即可。
时间复杂度:\(O(n)\)
参考代码:
//P2642
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int a[N], le[N], rt[N];
int n, cnt, sum;
int solve1() {//0011100111100
le[1] = a[1], rt[n] = a[n];
for (int i = 2; i <= n; ++i) le[i] = max(a[i], a[i] + le[i - 1]);
for (int i = 2; i <= n; ++i) le[i] = max(le[i], le[i - 1]);
for (int i = n - 1; i >= 1; --i) rt[i] = max(a[i], a[i] + rt[i + 1]);
for (int i = n - 1; i >= 1; --i) rt[i] = max(rt[i], rt[i + 1]);
int mx = INT_MIN;
for (int i = 1; i < n; ++i) mx = max(mx, le[i] + rt[i + 1]);
return mx;
}
int solve2() {//1110011100011
if (cnt == 1) {
int mx2 = INT_MIN, ans = 0;
for (int i = 1; i <= n; ++i) {
if (a[i] > 0) ans += a[i];
else mx2 = max(mx2, a[i]);
}
return ans + mx2;
}
for (int i = 1; i <= n; ++i)a[i] = -a[i];
return solve1() + sum;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
memset(le, -0x3f3f3f3f, sizeof(le));
memset(rt, -0x3f3f3f3f, sizeof(rt));
for (int i = 1; i <= n; ++i) {
cin >> a[i];
sum += a[i];
if (a[i] > 0) cnt++;
}
int res = solve1(), ans = solve2();
//cout << res << " " << ans << endl;
if (ans == 0) ans = INT_MIN;
res = max(res, ans);
cout << res << endl;
return 0;
}
关于上述问题可以看:P1121 环状最大两段子段和 题解 中第一篇题解关于最大子段和及其一些变式的解法
问题四
SP1043 GSS1 - Can you answer these queries I
题目描述:给你一个长度为\(n\)的数组\(a\),有\(q\)个询问,每个询问给出\(lr , rs\),求子数组\(a[lr...rs]\)的最大子数组,并输出其和。
数据范围:\(1\leq n ,q\leq 2 \times 10^5 ,1 \leq lr \leq rs \leq n\)
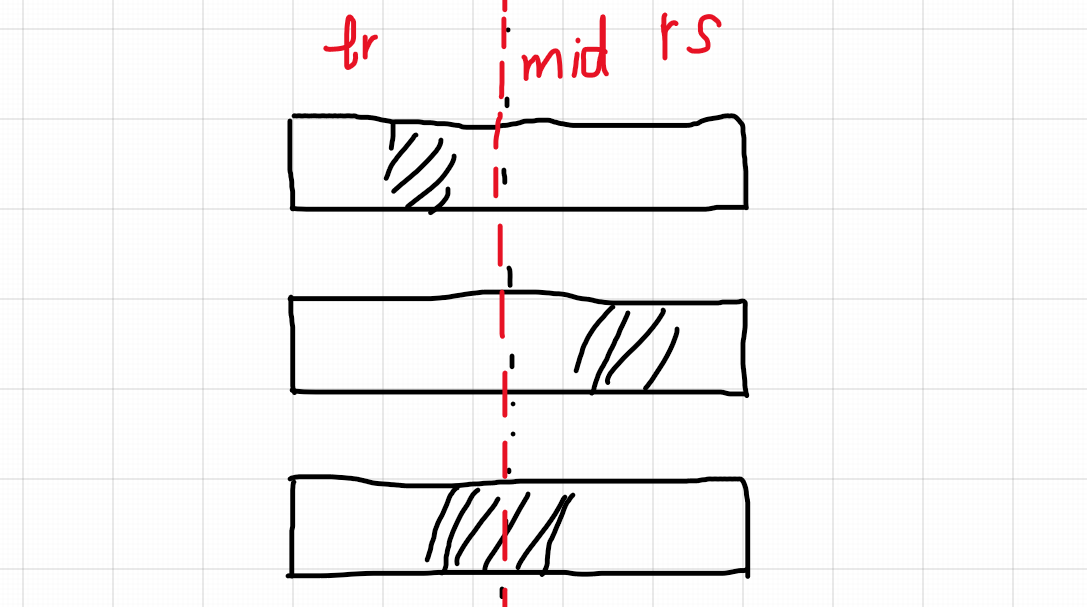
思路:显然我们可以使用线段树来维护该问题,考虑如何合并两个子数组,对于两个子数组合并后的新数组,其最大值只可能在原来的两个子数组中取得或者两个子数组各贡献一部分,显然就是合并的交界部分,所以我们需要对一个数组维护三个值:最大子数组和、最大前缀和、最大后缀和。向上合并的时候更新这三个值即可。
时间复杂度:\(O(nlogn)\)
参考代码:
#include<bits/stdc++.h>
#include<unordered_map>
#define for_int(i,a,b) for(int i=(a);i<=(b);++i)
#define rep_int(i,a,b) for(int i=(a);i>=(b);--i)
#define for_ll(i,a,b) for(ll i=(a);i<=(b);++i)
#define rep_ll(i,a,b) for(ll i=(a);i>=(b);--i)
#define Ios std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0)
#define ull unsigned long long
#define ll long long
#define int128 __int128
#define db double
#define PII std::pair<int,int>
#define PLI std::pair<long long , int>
template<class T> void chkmax(T& a, T b) { a > b ? (a = a) : (a = b); }
template<class T> void chkmin(T& a, T b) { a > b ? (a = b) : (a = a); }
template<class T> T min(T a, T b) { return a > b ? b : a; }
template<class T> T max(T a, T b) { return a < b ? b : a; }
template<class T> T abs(T a) { return a < 0 ? -a : a; }
//using namespace std;
/*
1.注意边界情况
2.优先考虑时间复杂度
!!! 3.求最大值时,答案应至多初始化为INT_MIN;求最小值时,答案应至少初始化为INT_MAX
4.遇事不决先暴力
5.代码要写简洁
6.计数题要开long long
*/
//快速IO
template<class T>
inline bool rd(T& ret) {
char c; int sgn;
if (c = getchar(), c == EOF) return 0;
while (c != '-' && (c < '0' || c > '9')) c = getchar();
sgn = (c == '-') ? -1 : 1;
ret = (c == '-') ? 0 : (c - '0');
while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
ret *= sgn;
return true;
}
template<class T>
inline void print(T x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
return;
}
using std::vector;
using std::queue;
using std::string;
using std::map;
using std::unordered_map;
using std::priority_queue;
using std::cout;
using std::cin;
using std::bitset;
struct SegmentTree {
int lr, rs, mid;
long long max, pre, next, sum;
};
const int N = 5e4 + 5;
SegmentTree tree[N << 2];
int a[N];
void pushUp(int rt) {
tree[rt].max = max(tree[rt << 1].max, tree[rt << 1 | 1].max);
tree[rt].pre = max(tree[rt << 1].pre, tree[rt << 1].sum + tree[rt << 1 | 1].pre);
tree[rt].next = max(tree[rt << 1 | 1].next, tree[rt << 1].next + tree[rt << 1 | 1].sum);
tree[rt].sum = tree[rt << 1].sum + tree[rt << 1 | 1].sum;
tree[rt].max = max(tree[rt].max, tree[rt << 1].next + tree[rt << 1 | 1].pre);
return;
}
void buildTree(int rt, int lr, int rs) {
tree[rt].lr = lr; tree[rt].rs = rs;
if (lr == rs) {
tree[rt].max = tree[rt].pre = a[lr];
tree[rt].sum = tree[rt].next = a[lr];
return;
}
int mid = tree[rt].mid = lr + rs >> 1;
buildTree(rt << 1, lr, mid);
buildTree(rt << 1 | 1, mid + 1, rs);
pushUp(rt);
return;
}
SegmentTree query(int rt, int lr, int rs) {
if (tree[rt].lr >= lr && tree[rt].rs <= rs) return tree[rt];
if (tree[rt].mid < lr) return query(rt << 1 | 1, lr, rs);
if (tree[rt].mid >= rs) return query(rt << 1, lr, rs);
SegmentTree res, left = query(rt << 1, lr, rs), right = query(rt << 1 | 1, lr, rs);
res.max = max(left.max, right.max);
res.pre = max(left.pre, left.sum + right.pre);
res.next = max(right.next, left.next + right.sum);
res.sum = left.sum + right.sum;
res.max = max(res.max, left.next + right.pre);
return res;
}
int n, q, lr, rs;
int main() {
rd(n);
for_int(i, 1, n) rd(a[i]);
buildTree(1, 1, n);
rd(q);
while (q--) {
rd(lr); rd(rs);
print(query(1, lr, rs).max); puts("");
}
return 0;
}
问题五
SP1716 GSS3 - Can you answer these queries III
题目描述:在问题四的基础上增加了单点修改操作
思路:显然在上述线段树代码中增加单点修改操作即可
时间复杂度:\(O(nlogn)\)
参考代码:
#include<bits/stdc++.h>
#include<unordered_map>
#define for_int(i,a,b) for(int i=(a);i<=(b);++i)
#define rep_int(i,a,b) for(int i=(a);i>=(b);--i)
#define for_ll(i,a,b) for(ll i=(a);i<=(b);++i)
#define rep_ll(i,a,b) for(ll i=(a);i>=(b);--i)
#define Ios std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0)
#define ull unsigned long long
#define ll long long
#define db double
#define PII std::pair<int,int>
#define PLI std::pair<long long , int>
template<class T> void chkmax(T& a, T b) { a > b ? (a = a) : (a = b); }
template<class T> void chkmin(T& a, T b) { a > b ? (a = b) : (a = a); }
template<class T> T min(T a, T b) { return a > b ? b : a; }
template<class T> T max(T a, T b) { return a < b ? b : a; }
template<class T> T abs(T a) { return a < 0 ? -a : a; }
//using namespace std;
/*
1.注意边界情况
2.优先考虑时间复杂度
!!! 3.求最大值时,答案应至多初始化为INT_MIN;求最小值时,答案应至少初始化为INT_MAX
4.遇事不决先暴力
5.代码要写简洁
6.计数题要开long long
*/
//快速IO
template<class T>
inline bool rd(T& ret) {
char c; int sgn;
if (c = getchar(), c == EOF) return 0;
while (c != '-' && (c < '0' || c > '9')) c = getchar();
sgn = (c == '-') ? -1 : 1;
ret = (c == '-') ? 0 : (c - '0');
while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
ret *= sgn;
return true;
}
template<class T>
inline void print(T x) {
if (x > 9) print(x / 10);
putchar(x % 10 + '0');
return;
}
using std::vector;
using std::queue;
using std::string;
using std::map;
using std::unordered_map;
using std::priority_queue;
using std::cout;
using std::cin;
using std::bitset;
const int N = 5e5 + 5;
struct Segment {
int lr, rs, mid;
int lrm, rsm, sum, val;
Segment() {
lr = 0; rs = 0; mid = 0; lrm = -10000000; rsm = -10000000; sum = -10000000; val = -10000000;
}
Segment operator += (const Segment& a) {
val = max(val, max(a.val, rsm + a.lrm));
lrm = max(lrm, sum + a.lrm);
rsm = max(a.rsm, a.sum + rsm);
sum += a.sum;
return *this;
}
};
Segment tree[N << 2];
int a[N];
void pushUp(int rt) {
tree[rt].sum = tree[rt << 1].sum + tree[rt << 1 | 1].sum;
tree[rt].lrm = max(tree[rt << 1].lrm, tree[rt << 1 | 1].lrm + tree[rt << 1].sum);
tree[rt].rsm = max(tree[rt << 1 | 1].rsm, tree[rt << 1 | 1].sum + tree[rt << 1].rsm);
tree[rt].val = max(tree[rt << 1].val, max(tree[rt << 1 | 1].val, tree[rt << 1].rsm + tree[rt << 1 | 1].lrm));
return;
}
void buildTree(int rt, int lr, int rs) {
tree[rt].lr = lr; tree[rt].rs = rs;
if (lr == rs) {
tree[rt].sum = tree[rt].val = a[lr];
tree[rt].lrm = tree[rt].rsm = a[lr];
return;
}
int mid = tree[rt].mid = lr + rs >> 1;
buildTree(rt << 1, lr, mid);
buildTree(rt << 1 | 1, mid + 1, rs);
pushUp(rt);
return;
}
void update(int rt, int pos, int val) {
if (tree[rt].lr > pos || tree[rt].rs < pos) return;
if (tree[rt].lr == tree[rt].rs) {
tree[rt].val = val; tree[rt].sum = val;
tree[rt].lrm = tree[rt].rsm = val;
return;
}
if (tree[rt].mid >= pos) update(rt << 1, pos, val);
else update(rt << 1 | 1, pos, val);
pushUp(rt);
return;
}
Segment query(int rt, int lr, int rs) {
if (tree[rt].lr >= lr && tree[rt].rs <= rs) return tree[rt];
if (tree[rt].mid >= lr && !(tree[rt].mid < rs)) return query(rt << 1, lr, rs);
if (!(tree[rt].mid >= lr) && tree[rt].mid < rs) return query(rt << 1 | 1, lr, rs);
Segment res;
Segment t1 = query(rt << 1, lr, rs);
Segment t2 = query(rt << 1 | 1, lr, rs);
res.sum = t1.sum + t2.sum;
res.lrm = max(t1.lrm, t1.sum + t2.lrm);
res.rsm = max(t2.rsm, t2.sum + t1.rsm);
res.val = max(t1.val, max(t2.val, t1.rsm + t2.lrm));
return res;
}
int n, m;
int op, lr, rs;
int main() {
rd(n);
for_int(i, 1, n) rd(a[i]);
buildTree(1, 1, n);
rd(m);
while (m--) {
rd(op); rd(lr); rd(rs);
if (op == 1) {
if (rs < lr) std::swap(lr, rs);
printf("%d\n", query(1, lr, rs).val);
}
else update(1, lr, rs);
}
return 0;
}
作者:cherish.
出处:https://home.cnblogs.com/u/cherish-/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号