DFS序

DFS序就是将树形结构转化成线性结构，使得树上对某一结点为根的子树的操作变成对一个区间的操作。

将树读入之后，进行\(dfs\),\(dfs\)过程中记录初始访问的时间戳\(intime\)和返回时的时间戳\(outtime\)，那么以该结点为子树的所有结点都在区间\([intime , outtime]\)内。每次对以该结点为根的子树的操作变成对区间\([intime , outtime]\)的操作。

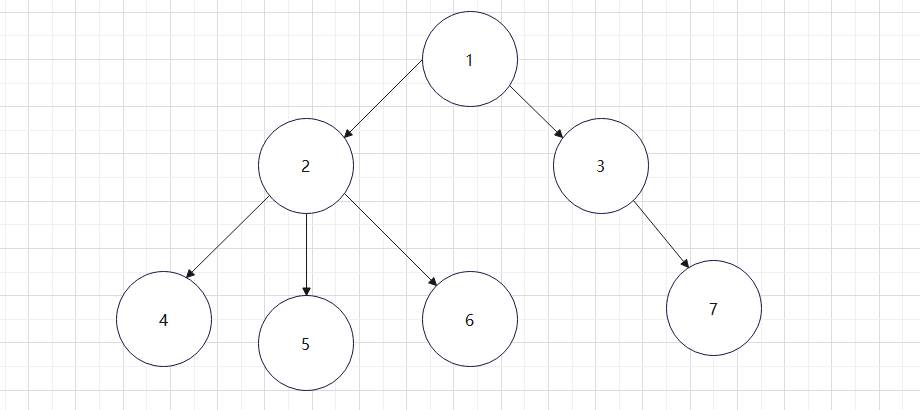
如对于上面这棵以\(1\)为根节点的树。则访问过程中的记录结果为：

dfs序	1	2	4	5	6	3	7
\(intime\)	1	2	3	4	5	6	7
\(outtime\)	7	5	3	4	5	7	7

然后我们只需要根据dfs序建立映射关系就可以将树形结构转化成线性结构了。

\(dfs\)参考代码：

int tim = 0;
void dfs(int u , int fa){
    intime[u] = ++tim;//记录初始访问的时间戳
    dfn[tim] = u;//记录dfs序的映射关系
    for(auto g : graph[u]){
        if(g == fa)continue;
        dfs(g, u);
    }
    outtime[u] = time;//记录访问完整棵树的时间戳
    return;
}

例题： 树上求和

题目描述： 给你一棵以\(1\)为根的有\(N\)个节点的树，有\(Q\)次操作。每次操作格式如下:

• \(1\; x \;y\) :将节点\(x\)所在的子树的所有节点的权值加上\(y\)
• \(2\;x\)询问\(x\)所在子树的所有节点的权值的平方和，答案模\(23333\)。

思路：根据题意，我们使用dfs序将树转化成线性结构，则就变成了一个经典的线段树维护区间加和区间求和操作，区间操作的范围为\([intime_x , outtime_x]\)。

关于线段树的维护：考虑对于一个数\(z\)，加上\(y\)后的平方值为:

\[(z + y)^2 = z^2 + 2xy + y^2 \]

其中\(2xy + y^2\)是增量。

对于区间\([lr,rs]\)来讲增量就是\(2y\sum_{i = lr}^{rs} x_i + (rs - lr + 1) * y^2\) ，所以线段树维护一个区间和，一个区间平方和即可。

时间复杂度：\(O(nlogn)\)

参考代码：

using std::vector;
using std::queue;
using std::string;
using std::map;
using std::unordered_map;
using std::priority_queue;
using std::cout;
using std::cin;
using std::bitset;
 
const int mod = 23333;
const int N = 1e5 + 5;
struct Tree{
    int sump , sum, tag , lr , rs;
};
Tree tree[N << 2];
int intime[N] , outtime[N] , dfn[N] , tim;
int a[N];
vector<vector<int>>graph(N);
void dfs(int u , int fa){
    intime[u] = ++tim;
    dfn[tim] = u;
    for(auto g : graph[u]){
        if(g == fa) continue;
        dfs(g , u);
    }
    outtime[u] = tim;
    return ;
}
void pushUp(int rt){
    tree[rt].sump = (tree[rt << 1].sump + tree[rt << 1 | 1].sump) % mod;
    tree[rt].sum = (tree[rt << 1 ].sum + tree[rt << 1 | 1].sum) % mod;
    return ;
}
void buildTree(int rt , int lr , int rs){
    tree[rt].sump = tree[rt].sum = tree[rt].tag = 0;
    tree[rt].lr = lr; tree[rt].rs = rs;
    if(lr == rs){
        tree[rt].sum = a[dfn[lr]];
        tree[rt].sump = a[dfn[lr]] * a[dfn[lr]] % mod;
        return ;
    }
    int mid = lr + rs >> 1;
    buildTree(rt << 1 , lr , mid);
    buildTree(rt << 1 | 1 , mid + 1 , rs);
    pushUp(rt);
    return ;
}
void pushDown(int rt){
    if(tree[rt].tag == 0) return ;
    int y = tree[rt].tag;
    int dy = 1ll * y * y % mod;
    tree[rt].tag = 0;
    (tree[rt << 1].tag += y) %= mod;
    (tree[rt << 1 | 1].tag += y ) %= mod;
     
    (tree[rt << 1].sump += (1ll * (tree[rt << 1].rs - tree[rt << 1].lr + 1) * dy % mod))%= mod;
    (tree[rt << 1].sump += (2ll * tree[rt << 1].sum * y % mod)) %= mod;
    (tree[rt << 1].sum += (1ll * (tree[rt << 1].rs - tree[rt << 1].lr + 1) * y % mod)) %= mod;
     
    (tree[rt << 1 | 1].sump += (1ll * (tree[rt << 1 | 1].rs - tree[rt << 1 | 1].lr + 1) * dy% mod))%= mod;
    (tree[rt << 1 | 1].sump += (2ll * tree[rt << 1 | 1].sum * y % mod)) %= mod;
    (tree[rt << 1 | 1].sum += (1ll * (tree[rt << 1 | 1].rs - tree[rt << 1 | 1].lr + 1) * y % mod)) %= mod;
    return ;
}
void Update(int rt , int lr , int rs , int y){
    int left = tree[rt].lr, right = tree[rt].rs;
    if(left > rs || right < lr) return ;
    if(left >= lr && right <= rs){
        int dy = 1ll * y * y % mod;
        (tree[rt].sump += (1ll * (tree[rt].rs - tree[rt].lr + 1) * dy % mod))%= mod;
        (tree[rt].sump += (2ll * tree[rt].sum * y % mod)) %= mod;
        (tree[rt].sum += (1ll * (tree[rt].rs - tree[rt].lr + 1) * y % mod)) %= mod;
        (tree[rt].tag += y) %= mod;
        return ;
    }
    pushDown(rt);
    int mid = left + right >> 1;
    if(mid >= lr) Update(rt << 1 , lr , rs , y);
    if(mid < rs) Update(rt << 1 | 1 , lr , rs , y);
    pushUp(rt);
    return ;
}
int query(int rt , int lr , int rs){
    int left = tree[rt].lr, right = tree[rt].rs;
    if(left > rs || right < lr) return 0;
    if(left >= lr && right <= rs) return tree[rt].sump;
    pushDown(rt);
    int mid = left + right >> 1;
    int res = 0;
    if(mid >= lr) res += query(rt << 1 , lr , rs);
    if(mid < rs) res += query(rt << 1 | 1, lr , rs);
    res %= mod;
    return res;
}
int n , m , u , v;
int op, x , y;
int main(){
    rd(n); rd(m);
    for_int(i,1,n) rd(a[i]), a[i] %= mod;
    for(int i = 1 ; i < n ; ++i){
        rd(u); rd(v);
        graph[u].push_back(v);
        graph[v].push_back(u);
    }
    dfs(1 , 0);
    buildTree(1 , 1 , n);
    while(m--){
        rd(op); rd(x);
        if(op == 1){
            rd(y);
            y %= mod;
            Update(1 , intime[x] , outtime[x] , y);
        }
        else printf("%d\n",query(1 , intime[x] , outtime[x]));
    }
    return 0;
}

练习题：

CF877E Danil and a Part-time Job: dfs序，然后用线段树维护区间信息

CF620E New Year Tree : dfs序+ 线段树，注意统计种数使用的是位运算进行标记