203.移除链表元素

203. 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

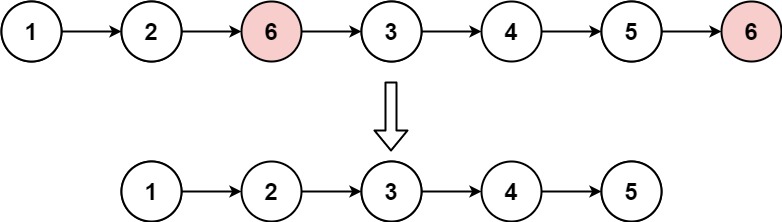
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

解题思路

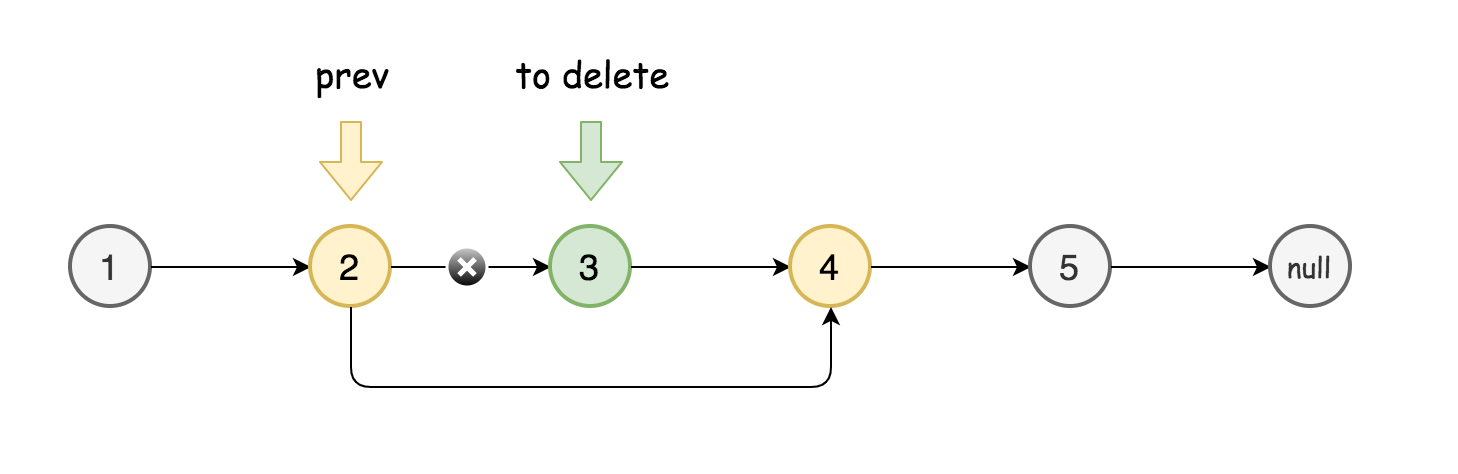
如果删除的节点是中间的节点，则问题非常简单：

• 选择要删除节点的前一个结点prev。
• 将prev的next设置为要删除结点的next。

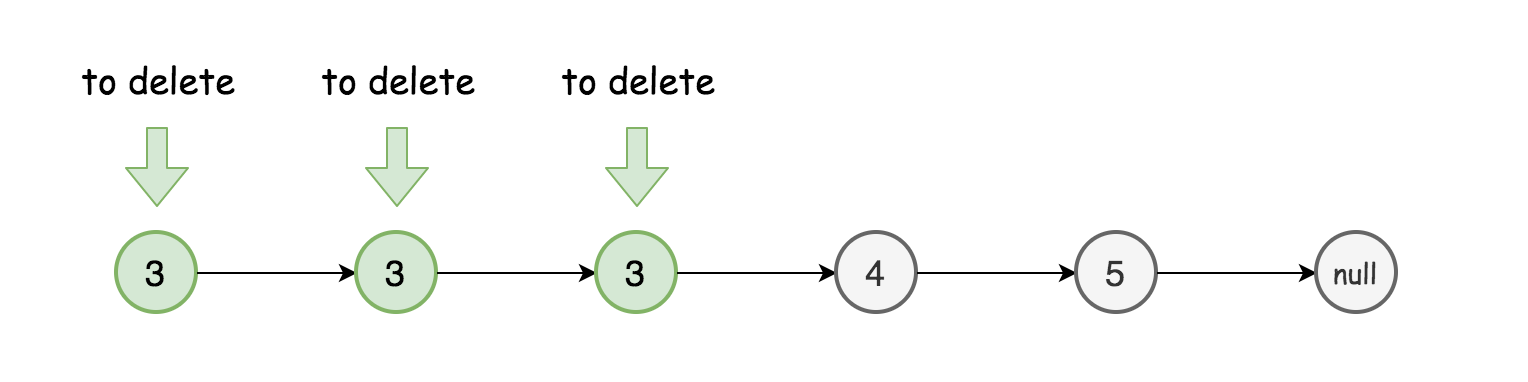
当要删除的一个或多个节点位于链表的头部时，事情会变得复杂：

可以通过哨兵节点去解决它，哨兵节点广泛应用于树和链表中，如伪头、伪尾、标记等，它们是纯功能的，通常不保存任何数据，其主要目的是使链表标准化，如使链表永不为空、永不无头、简化插入和删除。

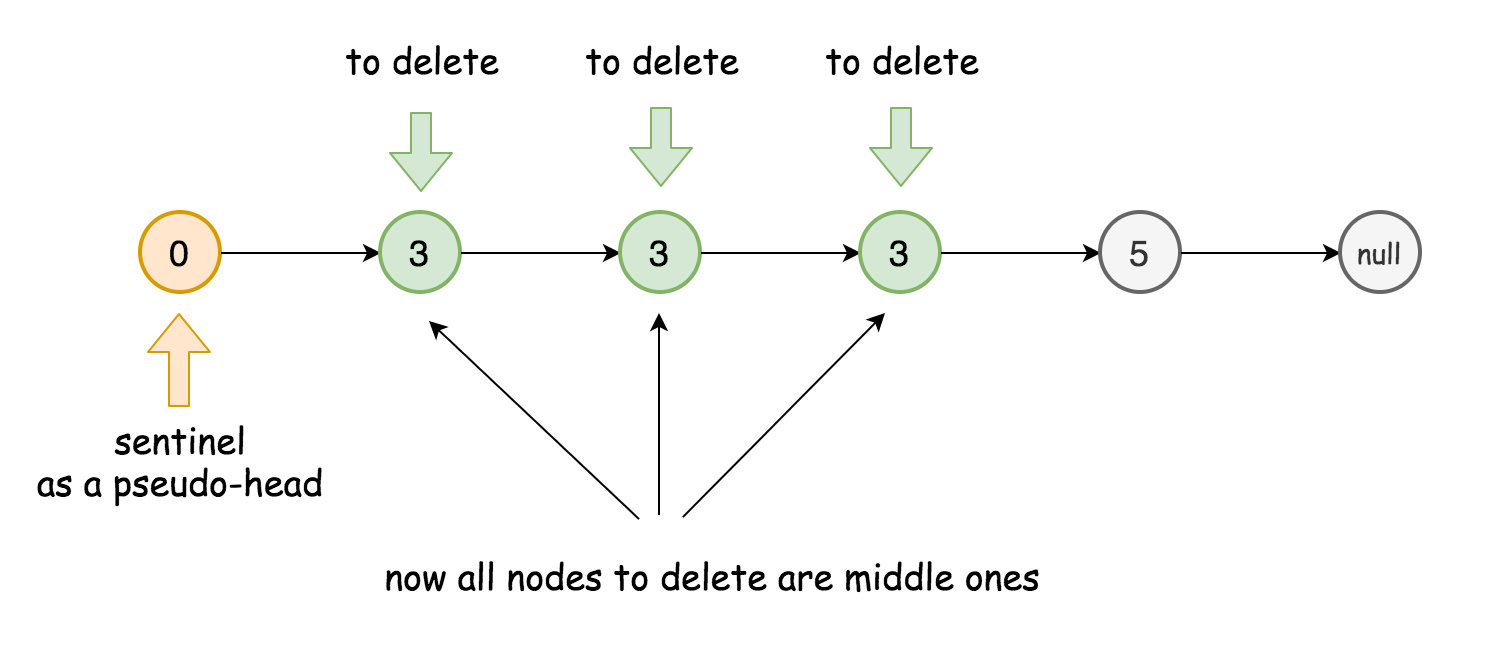
在这里哨兵节点将被用于伪头。

迭代

用 $\textit{temp} $表示当前节点。

• 如果 \(\textit{temp}\) 的下一个节点不为空且下一个节点的节点值等于给定的 \(\textit{val}\)，则需要删除下一个节点。

  删除下一个节点可以通过以下做法实现：\(\textit{temp}.\textit{next} = \textit{temp}.\textit{next}.\textit{next} \)

• 如果 \(\textit{temp}\) 的下一个节点的节点值不等于给定的 \(\textit{val}\)，则保留下一个节点，将 \(\textit{temp}\) 移动到下一个节点即可。

• 当 \(\textit{temp}\) 的下一个节点为空时，链表遍历结束，此时所有节点值等于 \(\textit{val}\) 的节点都被删除。

由于链表的头节点 \(\textit{head}\) 有可能需要被删除，因此创建哑节点 \(\textit{dummyHead}\)，令 \(\textit{dummyHead}.\textit{next} = \textit{head}\)，初始化 \(\textit{temp}=\textit{dummyHead}\)，然后遍历链表进行删除操作。最终返回 \(\textit{dummyHead}.\textit{next}\) 即为删除操作后的头节点。

代码实现

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode dummyHead = new ListNode(0);
        dummyHead.next = head;
        ListNode temp = dummyHead;
        
        while (temp.next != null) {
            if (temp.next.val == val) {
                temp.next = temp.next.next;
            } else {
                temp = temp.next;
            }
        }
        return dummyHead.next;
    }
}

复杂度分析

• 时间复杂度：\(O(n)\)，其中 \(n\) 是链表的长度。需要遍历链表一次。
• 空间复杂度：\(O(1)\)。

递归

链表的定义具有递归的性质，因此链表题目常可以用递归的方法求解。这道题要求删除链表中所有节点值等于特定值的节点，可以用递归实现。

对于给定的链表，首先对除了头节点 \(\textit{head}\) 以外的节点进行删除操作，然后判断 \(\textit{head}\) 的节点值是否等于给定的 \(\textit{val}\)。

• 如果 \(\textit{head}\) 的节点值等于 \(\textit{val}\)，则 \(\textit{head}\) 需要被删除，因此删除操作后的头节点为 \(\textit{head}.\textit{next}\)；
• 如果 \(\textit{head}\) 的节点值不等于 \(\textit{val}\)，则 \(\textit{head}\) 保留，因此删除操作后的头节点还是 \(\textit{head}\)。

上述过程是一个递归的过程。

递归的终止条件是 \(\textit{head}\) 为空，此时直接返回 \(\textit{head}\)；当 \(\textit{head}\) 不为空时，递归地进行删除操作，然后判断 \(\textit{head}\) 的节点值是否等于 \(\textit{val}\) 并决定是否要删除 \(\textit{head}\)。

代码实现

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        // 递归终止条件
        if (head == null) {
            return head;
        }
        head.next = removeElements(head.next, val);
        return head.val == val ? head.next : head;
    }
}

复杂度分析

时间复杂度：\(O(n)\)，其中 \(n\) 是链表的长度。递归过程中需要遍历链表一次。

空间复杂度：\(O(n)\)，其中 \(n\) 是链表的长度。空间复杂度主要取决于递归调用栈，最多不会超过 \(n\) 层。