84.柱状图中最大的矩形
题目
原题链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
给定\(n\)个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为\(1\)。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例:

以上是柱状图的示例,其中每个柱子的宽度为\(1\),给定的高度为[2,1,5,6,2,3]。
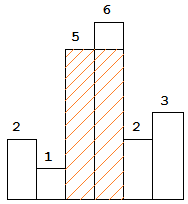
图中阴影部分为所能勾勒出的最大矩形面积,其面积为10个单位。
输入: [2,1,5,6,2,3]
输出: 10
注意:

解题思路
枚举高的方法:
-
首先枚举某一根柱子\(i\)作为高\(h = \textit{heights}[i]\)
-
随后需要进行向左右两边扩展,使得扩展到的柱子的高度均不小于\(h\)。即,需要找到左右两侧最近的高度小于\(h\)的柱子,这样这两根柱子之间(不包括其本身)的所有柱子高度均不小于\(h\),并且就是\(i\)能够扩展到的最远范围
如何求出一根柱子的左侧且最近的小于其高度的柱子?使用栈!
对于两根柱子\(j_0\)以及\(j_1\),如果\(j_0 < j_1\)并且\(\textit{heights}[j_0] \geq \textit{heights}[j_1]\),那么对于任意的在它们之后出现的柱子\(i\)(\(j_1 < i\)),\(j_0\)一定不会是\(i\)左侧且最近的小于其高度的柱子。
即,如果有两根柱子\(j_0\)和\(j_1\),其中\(j_0\)在\(j_1\)的左侧,并且\(j_0\)的高度大于等于\(j_1\),那么在后面的柱子\(i\)向左找小于其高度的柱子时,\(j_1\)会挡住\(j_0\),\(j_0\)就不会作为答案了。
这样一来,可以对数组从左向右进行遍历,同时维护一个栈,其中按照从小到大的顺序存放了一些\(j\)值。根据上面的结论,如果存放了\(j_0, j_1, \cdots, j_s\),那么一定有\(\textit{height}[j_0] < \textit{height}[j_1] < \cdots < \textit{height}[j_s]\),因为如果有两个相邻的\(j\)值对应的高度不满足\(<\)关系,那么后者会挡住前者,前者就不可能作为答案了。
例子:[6, 7, 5, 2, 4, 5, 9, 3],需要求出每一根柱子的左侧且最近的小于其高度的柱子。初始时的栈为空。(如果是元素是单调增的,则直接入栈,左方最近的小于其高度的柱子,在其左侧一位;如果单调减,则出栈,直至变成单调增,然后入栈,左方最近的小于其高度的柱子,在其左侧一位)
-
枚举6,因为栈为空,所以6左侧的柱子是
哨兵,位置为-1。随后将6入栈:- 栈:
[6(0)](这里括号内的数字表示柱子在原数组中的位置)
- 栈:
-
枚举7,由于\(6<7\),因此不会移除栈顶元素,所以7左侧的柱子是6,位置为
0。随后将7入栈:- 栈:
[6(0), 7(1)]
- 栈:
-
枚举5,由于\(7\geq 5\),因此移除栈顶元素7。同样地,\(6 \geq 5\),再移除栈顶元素6。此时栈为空,所以5左侧的柱子是
哨兵,位置为−1。随后将5入栈:- 栈:
[5(2)]
- 栈:
接下来的枚举过程也大同小异。
-
枚举2,移除栈顶元素5,得到2左侧的柱子是
哨兵,位置为−1。将2入栈:- 栈:
[2(3)]
- 栈:
-
枚举4、5和9,都不会移除任何栈顶元素,得到它们左侧的柱子分别是2、4和5,位置分别为3、4和5。将它们入栈:
- 栈:
[2(3), 4(4), 5(5), 9(6)]
- 栈:
-
枚举3,依次移除栈顶元素9、5和4,得到3左侧的柱子是2,位置为
3。将3入栈:- 栈:
[2(3), 3(7)]
- 栈:
这样一来,得到它们左侧的柱子编号分别为[-1, 0, -1, -1, 3, 4, 5, 3]。
用相同的方法,从右向左进行遍历,也可以得到它们右侧的柱子编号分别为[2, 2, 3, 8, 7, 7, 7, 8],这里将位置8看作哨兵。
在得到了左右两侧的柱子之后,就可以计算出每根柱子对应的左右边界,并求出答案了。
当从左向右或者从右向左遍历数组时,对栈的操作的次数就为\(O(N)\)。所以单调栈的总时间复杂度为\(O(N)\)。
代码实现
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Deque;
import java.util.LinkedList;
/**
* 84. 柱状图中最大的矩形
* @date 2021/5/17
* @author chenzufeng
*/
public class No84_LargestRectangle {
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String[] strings = reader.readLine().split(",");
int[] heights = new int[strings.length];
for (int i = 0; i < strings.length; i++) {
heights[i] = Integer.parseInt(strings[i]);
}
// System.out.println(Arrays.toString(heights));
System.out.println(largestRectangleArea(heights));
}
public static int largestRectangleArea(int[] heights) {
int length = heights.length;
// 从左向右遍历,每一根柱子左侧最近的小于其高度的柱子的位置
int[] left = new int[length];
// 从右向左遍历,每一根柱子右侧最近的小于其高度的柱子的位置
int[] right = new int[length];
// 使用栈去找左右两侧最近的高度小于当前高度的柱子
Deque<Integer> stack = new LinkedList<>();
// 找左侧最近的高度小于当前高度的柱子
for (int i = 0; i < length; i++) {
// 当栈不空,且将出现单调减,则出栈,直至变成单调增,然后入栈
while (! stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
stack.pop();
}
// 如果栈里是单调增的,则直接入栈,左方最近的小于其高度的柱子,在其左侧一位
left[i] = (stack.isEmpty() ? -1 : stack.peek());
stack.push(i);
}
stack.clear();
// 找右侧最近的高度小于当前高度的柱子
for (int i = length - 1; i >= 0; i--) { // 注意这里i从length - 1开始
// 当栈不空,且将出现单调减,则出栈,直至变成单调增,然后入栈
while (! stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
stack.pop();
}
// 如果栈里是单调增的,则直接入栈,右方最近的小于其高度的柱子,在其右侧一位
right[i] = (stack.isEmpty() ? length : stack.peek());
stack.push(i);
}
int ans = 0;
for (int i = 0; i < length; i++) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}
复杂度分析
- 时间复杂度:\(O(N)\)。
- 空间复杂度:\(O(N)\)。


