42.接雨水

题目

原题链接：https://leetcode-cn.com/problems/trapping-rain-water/

给定\(n\)个非负整数表示每个宽度为1的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接6个单位的雨水（蓝色部分表示雨水）。 

解题思路

维护一个单调栈，单调栈存储的是下标，满足从栈底到栈顶的下标对应的数组\(\textit{height}\)中的元素递减。

从左到右遍历数组，遍历到下标\(i\)时，如果栈内至少有两个元素，记栈顶元素为\(\textit{top}\)，\(\textit{top}\)的下面一个元素是\(\textit{left}\)，则一定有\(\textit{height}[\textit{left}] \ge \textit{height}[\textit{top}]\)。

如果\(\textit{height}[i]>\textit{height}[\textit{top}]\)，则得到一个可以接雨水的区域，该区域的宽度是\(i-\textit{left}-1\)，高度是 \(\min(\textit{height}[\textit{left}],\textit{height}[i])-\textit{height}[\textit{top}]\)，根据宽度和高度即可计算得到该区域能接的雨水量。为了得到\(\textit{left}\)，需要将\(\textit{top}\)出栈（此时\(\textit{height}[i]>\textit{height}[\textit{top}]\)）。在对\(\textit{top}\)计算能接的雨水量之后，\(\textit{left}\)变成新的\(\textit{top}\)，重复上述操作，直到栈变为空，或者栈顶下标对应的\(\textit{height}\)中的元素大于或等于\(\textit{height}[i]\)。

在对下标\(i\)处计算能接的雨水量之后，或者\(\textit{height}[i]<\textit{height}[\textit{top}]\)，则将\(i\)入栈，继续遍历后面的下标，计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。

注意：

\(3,4,5\)依次入栈后，由于\(6\)的高度比\(5\)高，所以\(5\)要出栈，此时计算得到雨量为1：

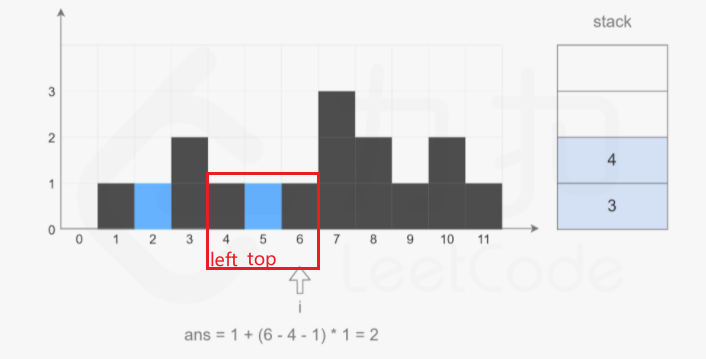
由于\(6\)的高度和\(4\)的高度一致，所以\(6\)入栈。接着，由于\(7\)的高度比\(6\)的高度高，所以\(6\)出栈，然后计算水量为\(0\)：

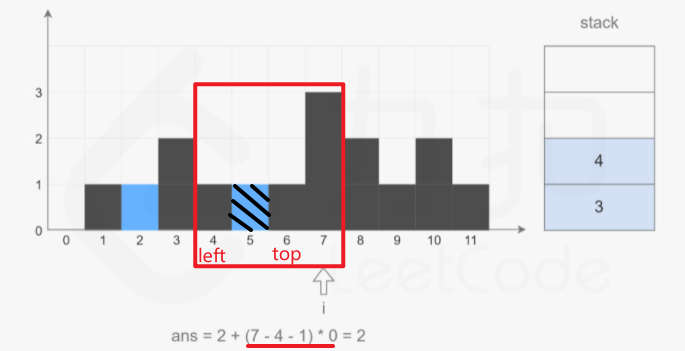
接着\(4\)出栈：

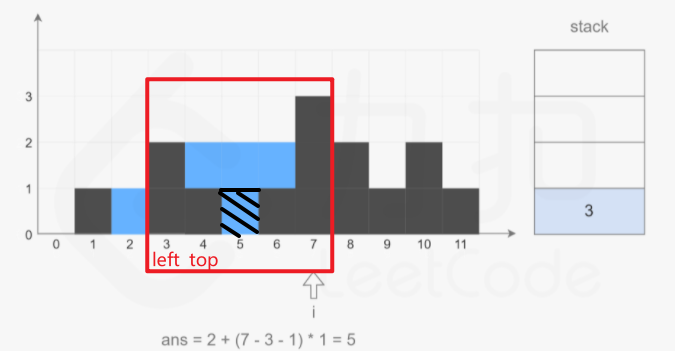
代码实现

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Deque;
import java.util.LinkedList;

/**
 * 42.接雨水
 * @date 2021/5/17
 * @author chenzufeng
 */

public class No42_TrappingRainWater {
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String[] strings = reader.readLine().split(",");
        int[] heights = new int[strings.length];
        for (int i = 0; i < strings.length; i++) {
            heights[i] = Integer.parseInt(strings[i]);
        }

        System.out.println(trap(heights));
    }

    public static int trap(int[] heights) {
        int ans = 0;
        int length = heights.length;
        Deque<Integer> stack = new LinkedList<>();

        for (int i = 0; i < length; i++) {
            // 当栈不为空，且新d高度大于栈顶所对应的墙高度
            while (! stack.isEmpty() && heights[i] > heights[stack.peek()]) {
                int top = stack.pop();
                // 栈中仅有一个元素，抛出后为空栈
                if (stack.isEmpty()) {
                    break;
                }

                // 栈中至少有两个元素：抛出一个后还有一个
                int left = stack.peek();

                // 计算雨水量
                int currentWidth = i - left - 1;
                int currentHeight = Math.min(heights[left], heights[i]) - heights[top];
                ans += currentHeight * currentWidth;
            }

            // 新高度小于或等于栈顶所对应的高度直接入栈，或者计算完雨量后，新高度入栈
            stack.push(i);
        }

        return ans;
    }
}

复杂度分析

时间复杂度：\(O(n)\)，其中\(n\)是数组\(\textit{height}\)的长度。从\(0\)到\(n-1\)的每个下标最多只会入栈和出栈各一次。

空间复杂度：\(O(n)\)，其中\(n\)是数组\(\textit{height}\)的长度。空间复杂度主要取决于栈空间，栈的大小不会超过\(n\)。