排序
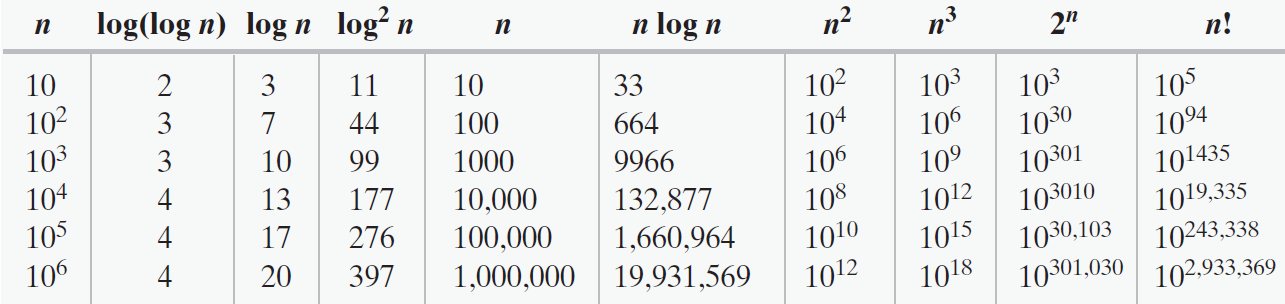
排序效率对比

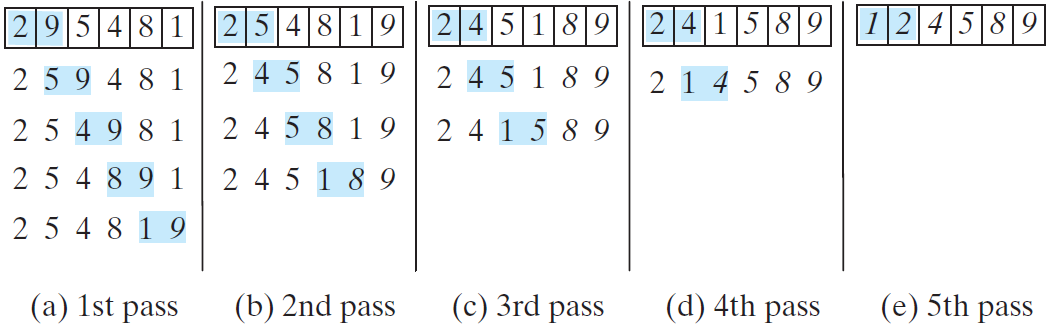
冒泡排序
将数组中相邻的两个数进行比较,较小的数值向下沉,数值比较大的向上浮。

算法实现
package sort;
public class BubbleSort {
/**
* 设置标志位needNextPass,如果发生了交换needNextPass设置为true;如果没有交换就设置为false。
* 这样当一轮比较结束后,如果needNextPass仍为false
* 即:这一轮没有发生交换,说明数据的顺序已经排好,没有必要继续进行下去。
* @param arr
* @param <T>
*/
public static <T extends Comparable<? super T>> void bubbleSort(T[] arr) {
boolean needNextPass;
// 共length位元素,需length - 1次排序
for (int i = 1; i < arr.length; i++) {
needNextPass = false;
// 每一次排序需arr.length - i - 1次比较
System.out.printf("第%d次排序\n", i);
for (int j = 0; j < arr.length - i; j++) {
if (arr[j].compareTo(arr[j + 1]) > 0) {
needNextPass = true;
swap(arr, j, j + 1);
}
}
// 如果needNextPass仍为false,这一轮没有发生交换,说明数据的顺序已经排好
if (!needNextPass) {
break;
}
}
}
private static void swap(Object[] arr, int i, int j) {
Object temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试代码:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class TestBubbleSort {
public static void main(String[] args) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("请输入待排序的数");
String[] strings = reader.readLine().split(" ");
Integer[] arr = new Integer[strings.length];
for (int i = 0; i < strings.length; i++) {
arr[i] = Integer.parseInt(strings[i]);
}
BubbleSort.bubbleSort(arr);
System.out.println("\n排序后:");
for (Integer integer : arr) {
System.out.print(integer + " ");
}
} catch (IOException e) {
e.printStackTrace();
}
}
}
算法效率
时间复杂度为\(O(n^2)\)。
选择排序
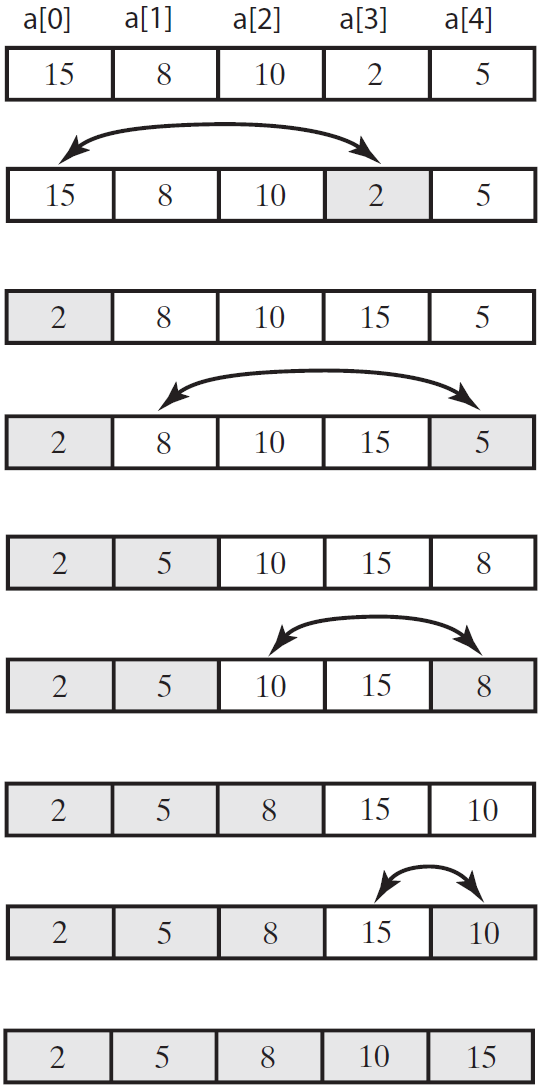
从数组中选择最小元素,将它与数组的第一个元素交换位置。再从数组剩下的元素中选择出最小的元素,将它与数组的第二个元素交换位置。不断进行这样的操作,直到将整个数组排序。

算法实现
package sort;
public class SelectionSort {
/**
* Sorts n objects in an array into ascending order.
* @param arr
* @param length 数组的长度
* @param <T>
*/
public static <T extends Comparable<? super T>> void selectionSort(T[] arr, int length) {
// 只需要找length - 1次
for (int index = 0; index < length - 1; index++) {
// 最后一个数index = length - 1
int indexOfNextSmallest = getIndexOfSmallest(arr, index, length - 1);
swap(arr, index, indexOfNextSmallest);
}
}
private static void swap(Object[] arr, int i, int j) {
Object temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
private static <T extends Comparable<? super T>> int getIndexOfSmallest(T[] arr, int first, int last) {
T min = arr[first];
int indexOfMin = first;
// index要取到last:index <= last
for (int index = first + 1; index <= last; index++) {
if (arr[index].compareTo(min) < 0) {
min = arr[index];
indexOfMin = index;
}
}
return indexOfMin;
}
}
测试代码:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class TestSelectionSort {
public static void main(String[] args) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
/*
System.out.println("请输入数组元素的个数及相应的元素:")
读取第一行参数
int length = Integer.parseInt(reader.readLine())
*/
System.out.println("请输入待排序的数:");
String[] str = reader.readLine().split(" ");
// 转化成数组
Integer[] arr = new Integer[str.length];
for (int i = 0; i < str.length; i++) {
arr[i] = Integer.parseInt(str[i]);
}
SelectionSort.selectionSort(arr, str.length);
System.out.println("\n排序后:");
for (Integer num : arr) {
System.out.print(num + " ");
}
} catch (IOException e) {
e.printStackTrace();
}
}
}
算法效率
时间复杂度为\(O(n^2)\);不论数组中项的初始次序如何,都需要\(O(n^2)\)次比较,但它仅执行\(O(n)\)次交换!
插入排序
举例理解:打扑克牌顺牌!
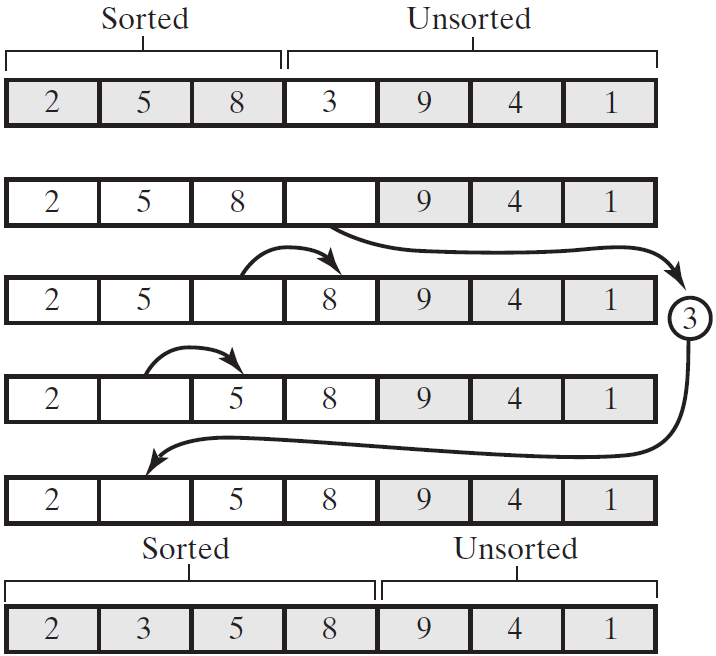
对数组的插入排序,将数组分隔(partition) (即划分)为两部分。第一部分是有序的,初始时仅含有数组中的第一项。第二部分含有其余的项。算法从未排序部分移走第一项,并将它插入有序部分中合适的有序位置。从有序部分的末尾开始,朝着开头方向,通过将待排序项与各有序项进行比较来选择合适的位置。当比较时,将有序部分的数组项右移,为插入腾出空间。
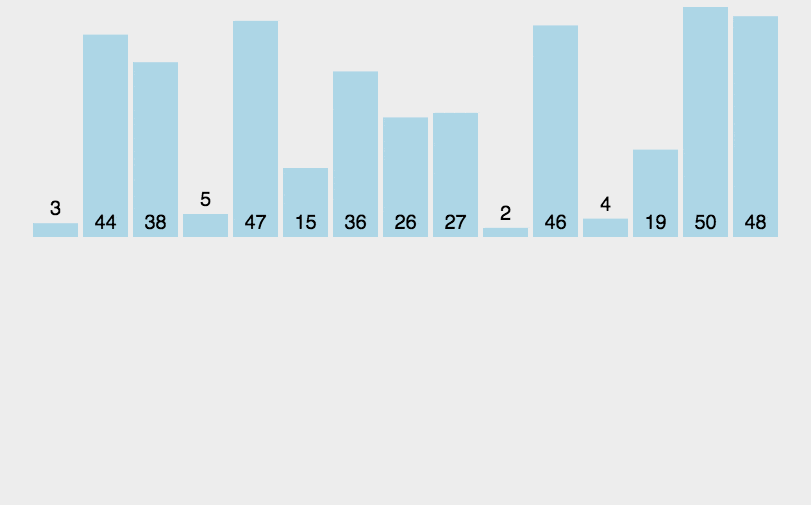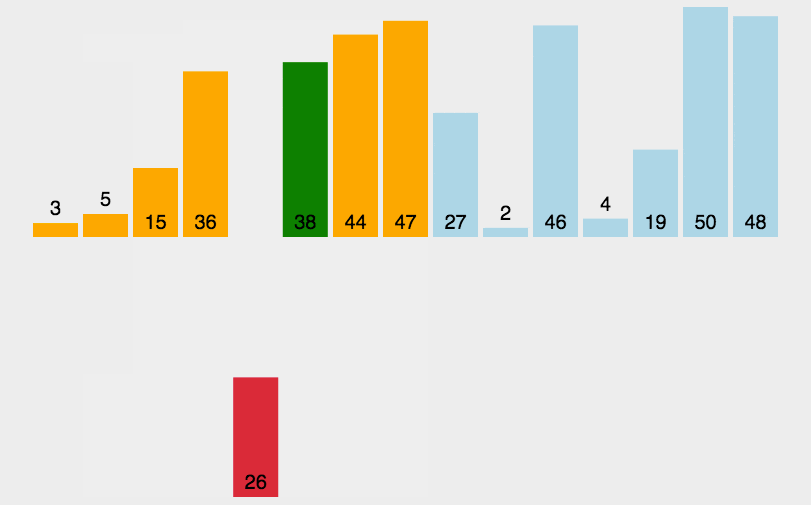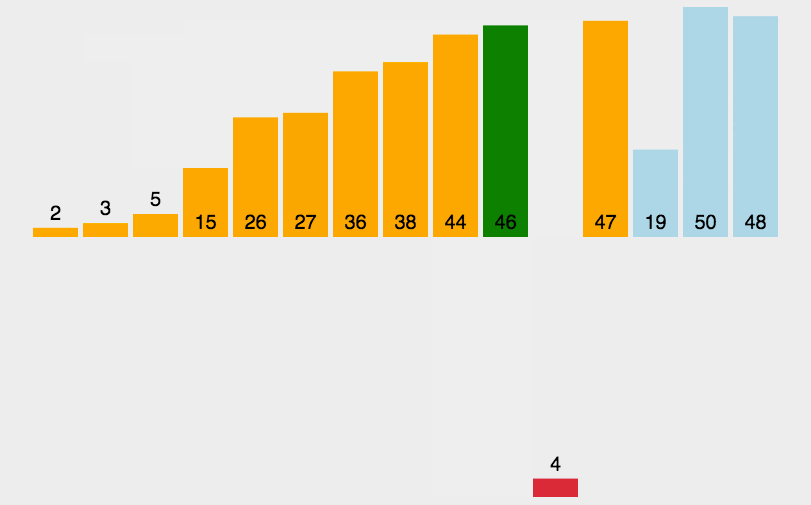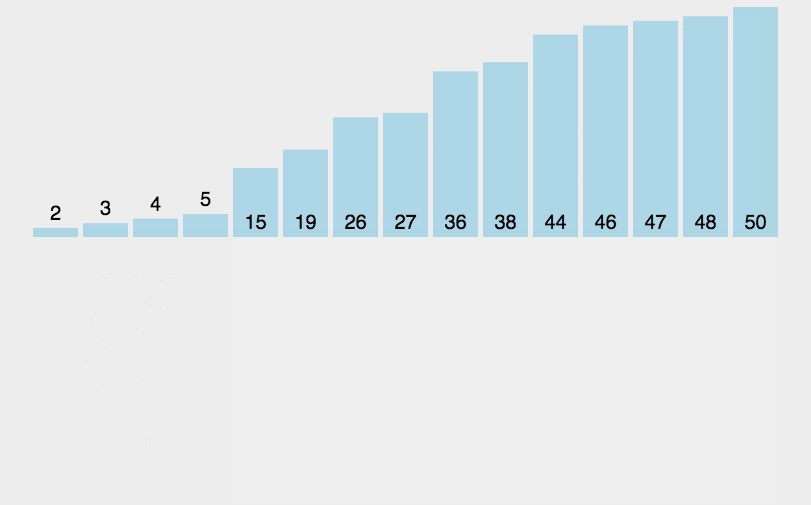
算法实现
package sort;
public class InsertionSort {
/**
* 可以理解为顺牌
* @param arr
* @param <T>
*/
public static <T extends Comparable<? super T>> void insertionSort(T[] arr) {
for (int i = 1; i < arr.length; i++) {
T insertedValue = arr[i];
int j;
for (j = i - 1; j >= 0 && insertedValue.compareTo(arr[j]) < 0; j--) {
// arr[j + 1]就是当前要顺的牌;
// 把牌往后移
arr[j + 1] = arr[j];
}
// 由于j--,要插入的位置是j + 1
arr[j + 1] = insertedValue;
}
}
}
测试代码:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class TestInsertionSort {
public static void main(String[] args) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("请输入待排序元素:");
String[] strings = reader.readLine().split(" ");
Integer[] arr = new Integer[strings.length];
for (int i = 0; i < strings.length; i++) {
arr[i] = Integer.parseInt(strings[i]);
}
InsertionSort.insertionSort(arr);
System.out.println("排序后:");
for (Integer integer : arr) {
System.out.print(integer + " ");
}
} catch (IOException e) {
e.printStackTrace();
}
}
}
算法效率
时间复杂度为\(O(n^2)\);
最优时插入排序是\(O(n)\),最坏时是\(O(n^2)\)。数组越接近有序,插入排序要做的工作越少。
希尔排序
希尔排序是插入排序的变体。在插入排序过程中,数组项只移动到相邻位置。当项与正确的有序位置相距甚远时,它必须进行很多次这样的移动。所以当数组完全无序时,插入排序要花很多时间。但当数组基本有序时,插入排序有很好的效率。
希尔排序的思想是,使数组中任意间隔为\(h\)的元素都是有序的,也就意味着,一个\(h\)有序数组就是\(h\)个相互独立的有序数组编织在一起组成的一个数组。
下图显示了一个数组及每隔5项组成的子数组。第一个子数组含有整数10、9和7;第二个子数组含有16和6;等等。
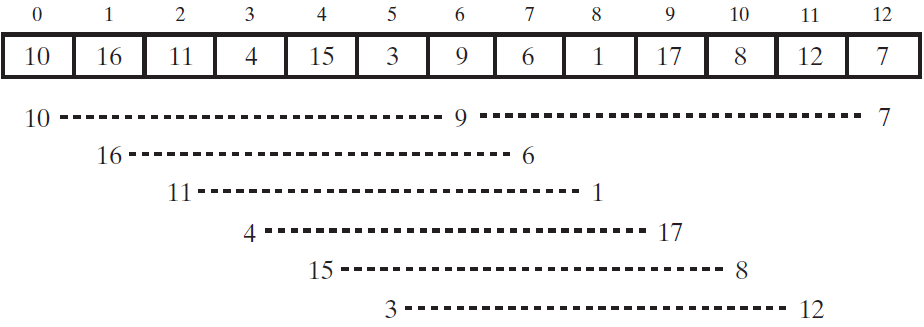
现在使用插入排序分别对这6个子数组进行排序,排序后数组比原始状态“更有序”了:
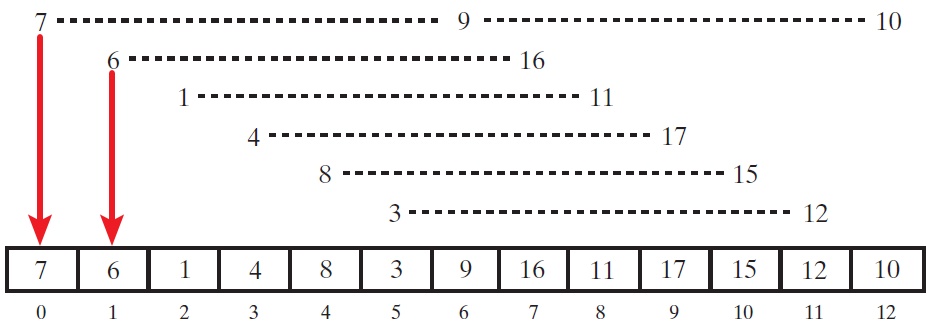
现在形成新的子数组,这次减小下标之间的间隔。Shell建议子数组下标间隔是\(n/2\),且每趟排序中这个值减半直到为1。示例数组有13项,所以从间隔为6开始。现在将间隔减小到3:

对得到的三个子数组进行插入排序:
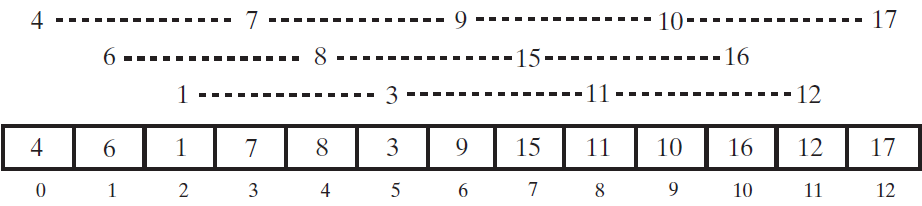
将当前间隔3除以2得到1,所以最后一步只是对整个数组进行普通的插入排序。

算法实现
package sort;
public class ShellSort {
public static <T extends Comparable<? super T>> void shellSort(T[] arr) {
int separation = arr.length / 2;
while (separation > 0) {
// 将数组分成separation个子数组进行插入排序
// 注意:begin <= separation - 1;当separation=1时,进行最后一次插入排序
for (int begin = 0; begin <= separation - 1; begin++) {
incrementalInsertionSort(arr, begin, separation);
}
separation /= 2;
}
}
/**
* 对每个子数组进行插入排序
*
* @param arr
* @param first
* @param separation 普通插入排序的间隔为1,这里为separation
* @param <T>
*/
private static <T extends Comparable<? super T>>
void incrementalInsertionSort(T[] arr, int first, int separation) {
for (int i = first + separation; i < arr.length; i += separation) {
T insertedValue = arr[i];
int j;
for (j = i - separation; j >= 0 && insertedValue.compareTo(arr[j]) < 0; j -= separation) {
// arr[j + separation] 就是当前抓到的牌;把牌往后移
arr[j + separation] = arr[j];
}
// 由于j -= separation,要插入的位置是j + separation
arr[j + separation] = insertedValue;
}
}
}
测试代码:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class TestShellSort {
public static void main(String[] args) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("请输入待排序元素:");
String[] strings = reader.readLine().split(" ");
Integer[] arr = new Integer[strings.length];
for (int i = 0; i < strings.length; i++) {
arr[i] = Integer.parseInt(strings[i]);
}
ShellSort.shellSort(arr);
System.out.println("排序后:");
for (Integer integer : arr) {
System.out.print(integer + " ");
}
} catch (IOException e) {
e.printStackTrace();
}
}
}
希尔排序效率

虽然使用了多次插入排序而不是仅用一次,但对数组最初的排序远比原始数组要小得多,后来的排序是对部分有序的数组进行的,且最后的排序是对几乎全部有序的数组进行的。
因为incrementalInsertionSort方法涉及一个循环,而本身又是在嵌套的循环内被调用,所以希尔排序使用了3层嵌套的循环。这样的算法常常是\(O(n^3)\)的。但可以证明希尔排序的最坏情形仍是\(O(n^2)\) 的。如果\(n\)是2的幂次.则平均情形是\(O(n^{1.5})\)。如果稍稍调整一下间隔,能使希尔排序的效率更高——当separation为偶数时,将其加1,则最坏情形可以改进为\(O(n^{1.5})\)。
归并排序
归并排序算法将数组分为两半,对每部分递归地应用归并排序。在两部分都排好序后,对它们进行归并。该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
持续将数组划分为子数组,直到每个子数组只包含一个元素。然后,该算法将这些小的子数组归并为稍大的有序子数组,直到最后形成一个有序的数组。
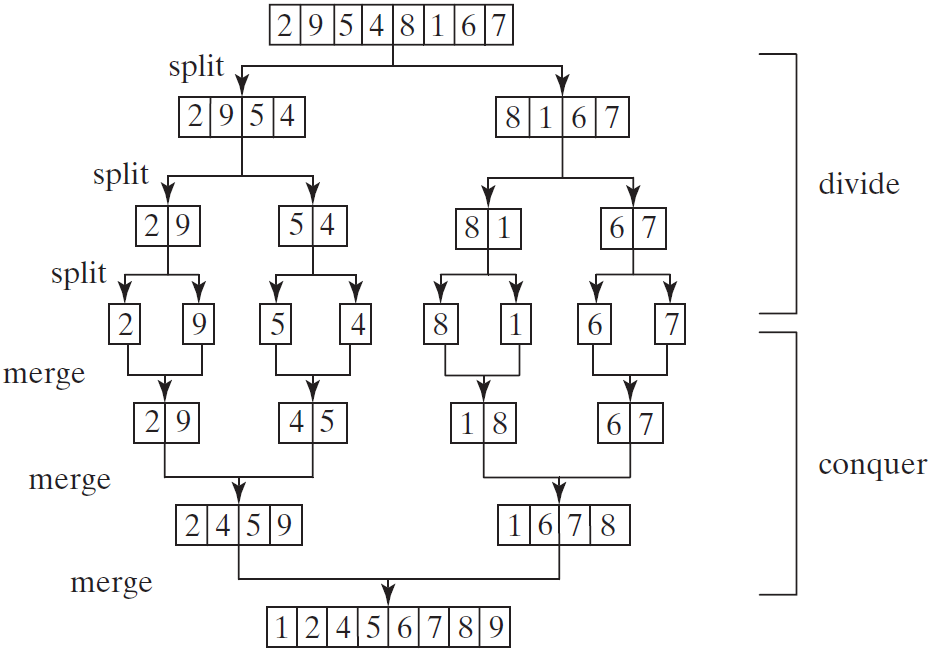
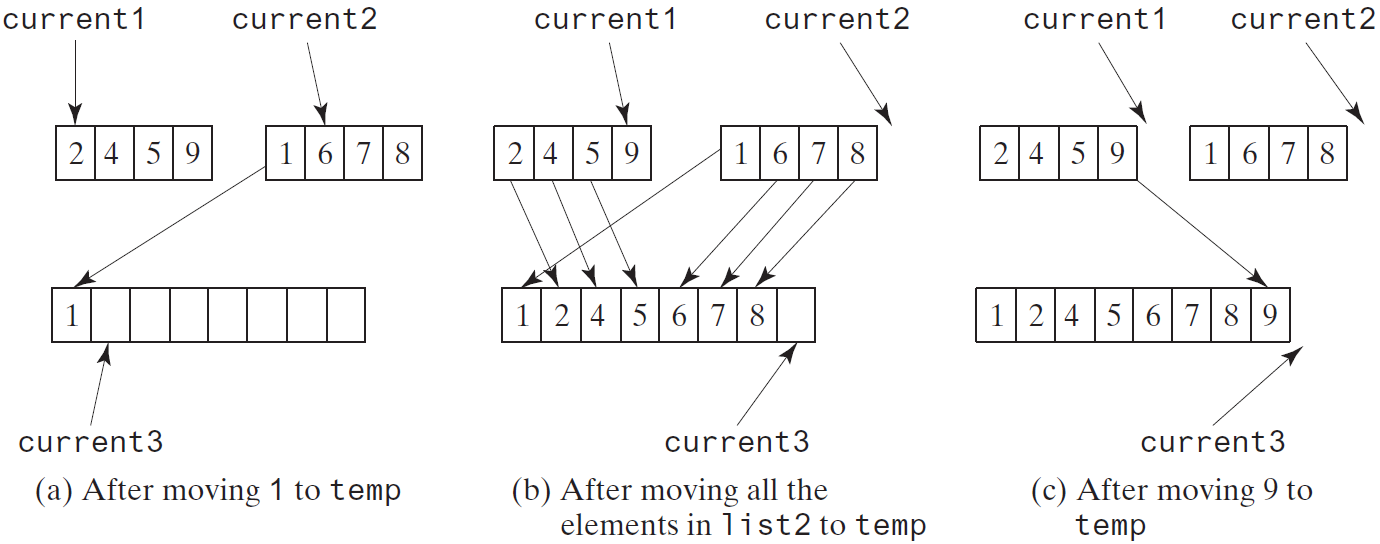
将两个有序数组归并为一个有序数组:
private static void merge(int[] list1, int[] list2, int[] temp)
{
int current1 = 0; // Current index in list1
int current2 = 0; // Current index in list2
int current3 = 0; // Current index in temp
while (current1 < list1.length && current2 < list2.length)
{
if (list1[current1] < list2[current2])
temp[current3++] = list1[current1++];
else
temp[current3++] = list2[current2++];
}
while (current1 < list1.length)
temp[current3++] = list1[current1++];
while (current2 < list2.length)
temp[current3++] = list2[current2++];
}
箭头上的数字表示递归调用及合并的次序:

算法实现
package sort;
public class MergeSort {
public static <T extends Comparable<? super T>> void mergeSort(T[] arr) {
if (arr.length > 1) {
// Divide the first half
@SuppressWarnings("unchecked")
T[] firstHalf = (T[]) new Comparable<?>[arr.length / 2];
System.arraycopy(arr, 0, firstHalf, 0, arr.length / 2);
mergeSort(firstHalf);
// Divide the second half
int secondHalfLength = arr.length - arr.length / 2;
@SuppressWarnings("unchecked")
T[] secondHalf = (T[]) new Comparable<?>[secondHalfLength];
System.arraycopy(arr, arr.length / 2, secondHalf, 0, secondHalfLength);
mergeSort(secondHalf);
// Merge firstHalf and secondHalf into one arr
merge(firstHalf, secondHalf, arr);
}
}
private static <T extends Comparable<? super T>> void merge(T[] arr1, T[] arr2, T[] temp) {
// Current index in arr1, arr2, temp
int currentIndex1 = 0;
int currentIndex2 = 0;
int currentIndex3 = 0;
while (currentIndex1 < arr1.length && currentIndex2 < arr2.length) {
if (arr1[currentIndex1].compareTo(arr2[currentIndex2]) < 0) {
temp[currentIndex3++] = arr1[currentIndex1++];
} else {
temp[currentIndex3++] = arr2[currentIndex2++];
}
}
while (currentIndex1 < arr1.length) {
temp[currentIndex3++] = arr1[currentIndex1++];
}
while (currentIndex2 < arr2.length) {
temp[currentIndex3++] = arr2[currentIndex2++];
}
}
}
测试代码:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class TestMergeSort {
public static void main(String[] args) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("请输入待排元素:");
String[] strings = reader.readLine().split(" ");
Integer[] arr = new Integer[strings.length];
for (int i = 0; i < strings.length; i++) {
arr[i] = Integer.parseInt(strings[i]);
}
MergeSort.mergeSort(arr);
System.out.println("排序后:");
for (Integer integer : arr) {
System.out.print(integer + " ");
}
} catch (IOException e) {
e.printStackTrace();
}
}
}
算法效率
归并排序的时间复杂度在所有情形下都为\(O\left(n\log n\right)\),优于冒泡排序、选择排序和插入排序。它对临时数组的需求(在合并阶段)是它的缺点。
java.util.Arrays类中的sort方法是使用归并排序算法的变体来实现的。
快速排序
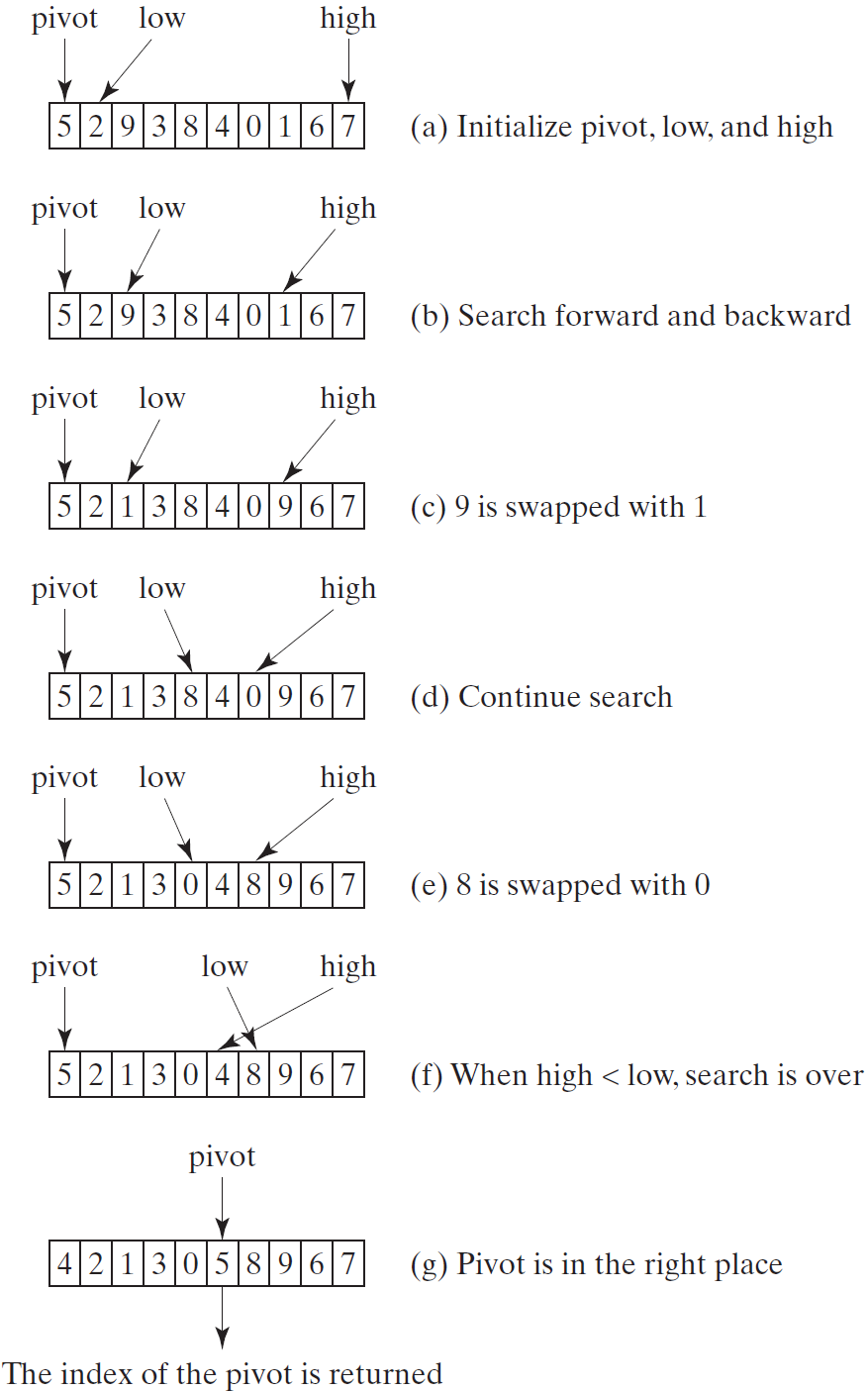
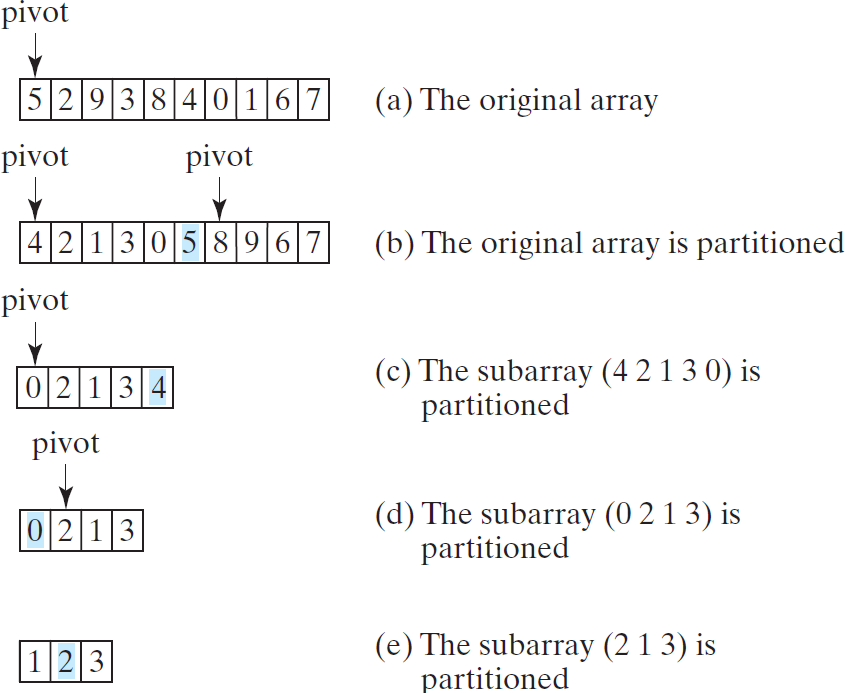
在数组中选择一个称为主元(pivot)的元素,将数组分为两部分,使得第一部分中的所有元素都小于或等于主元,而笫二部分中的所有元素都大于主元。然后对第一部分递归地应用快速排序算法,然后对笫二部分递归地应用快速排序算法。
主元的选择会影响算法的性能。在理想情况下,应该选择能平均划分两部分的主元。为了简单起见,假定将数组的第一个元素选为主元。
一次快速排序:
对子数组进行快速排序:
算法实现
package sort;
public class QuickSort {
public static <T extends Comparable<? super T>> void quickSort(T[] arr) {
quickSort(arr, 0, arr.length - 1);
}
private static <T extends Comparable<? super T>> void quickSort(T[] arr, int first, int last) {
if (last > first) {
int pivotIndex = getPivotIndex(arr, first, last);
quickSort(arr, first, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, last);
}
}
private static <T extends Comparable<? super T>> int getPivotIndex(T[] arr, int low, int high) {
T pivot = arr[low];
int i = low;
int j = high + 1;
while (true) {
while (arr[++i].compareTo(pivot) < 0) {
if (i == high) {
break;
}
}
while (arr[--j].compareTo(pivot) > 0) {
if (j == low) {
break;
}
}
if (i >= j) {
break;
}
exchange(arr, i, j);
}
exchange(arr, low, j);
return j;
}
private static void exchange(Object[] arr, int i, int j) {
Object temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
测试代码:
package sort;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class TestQuickSort {
public static void main(String[] args) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("请输入待排序元素:");
String[] strings = reader.readLine().split(" ");
Integer[] arr = new Integer[strings.length];
for (int i = 0; i < strings.length; i++) {
arr[i] = Integer.parseInt(strings[i]);
}
QuickSort.quickSort(arr);
System.out.println("排序后:");
for (Integer integer : arr) {
System.out.print(integer + " ");
}
} catch (IOException e) {
e.printStackTrace();
}
}
}
算法效率
快速排序在平均情形下是\(O(nlogn)\),但在最坏情况下是\(O(n^2)\)。pivot(枢轴)的选择对快速排序的效率有影响!


