54. 螺旋矩阵

题目

原题链接：https://leetcode-cn.com/problems/spiral-matrix/

给你一个m行n列的矩阵matrix，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

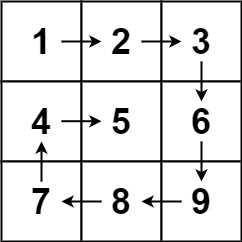
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

解题思路

可以将矩阵看成若干层，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素。
定义矩阵的第\(k\)层：例如，下图矩阵最外层元素都是第\(1\)层，次外层元素都是第\(2\)层，剩下的元素都是第\(3\)层

[[1, 1, 1, 1, 1, 1, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 2, 3, 3, 3, 2, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 1, 1, 1, 1, 1, 1]]

对于每层，从左上方开始以顺时针的顺序遍历所有元素。假设当前层的左上角位于$ (\textit{top}, \textit{left})$，右下角位于 \((\textit{bottom}, \textit{right})\)，按照如下顺序遍历当前层的元素：

• 从左到右遍历上侧元素，依次为 \((\textit{top}, \textit{left})\)\(\rightarrow\)\((\textit{top}, \textit{right})\)。

• 从上到下遍历右侧元素，依次为\((\textit{top} + 1, \textit{right})\)\(\rightarrow\)\((\textit{bottom}, \textit{right})\)。

• 如果\(\textit{left} < \textit{right}\)且\(\textit{top} < \textit{bottom}\)，则从右到左遍历下侧元素，依次为\((\textit{bottom}, \textit{right} - 1)\)\(\rightarrow\)\((\textit{bottom}, \textit{left})\)，以及从下到上遍历左侧元素，依次为\((\textit{bottom}-1, \textit{left})\)\(\rightarrow\) \((\textit{top} + 1, \textit{left})\)。

遍历完当前层的元素之后，将\(\textit{left}\)和\(\textit{top}\)分别增加\(1\)，将\(\textit{right}\)和\(\textit{bottom}\)分别减少\(1\)，进入下一层继续遍历，直到遍历完所有元素为止。

代码实现

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;

/**
 * 54.螺旋矩阵
 * 按照顺时针螺旋顺序，返回m*n矩阵中的所有元素
 * @author chenzufeng
 */
public class No54_SpiralMatrix {
    public static void main(String[] args) {
        try {
            BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
            String[] info = reader.readLine().split(" ");
            int rows = Integer.parseInt(info[0]);
            int columns = Integer.parseInt(info[1]);
            int[][] matrix = new int[rows][columns];

            for (int i = 0; i < rows; i++) {
                String[] rowStr = reader.readLine().split(",");
                for (int j = 0; j < columns; j++) {
                    matrix[i][j] = Integer.parseInt(rowStr[j]);
                }
            }

            for (int i : spiralOrder(matrix)) {
                System.out.print(i + ",");
            }

        } catch (IOException e) {
            e.printStackTrace();
        }
    }

    public static List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> result = new ArrayList<>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return result;
        }

        // 初始化行和列，上下左右index
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;

        while (left <= right && top <= bottom) {
            // 1.顶部行——从左到右，列column在变，边界为left到right
            for (int column = left; column <= right; column++) {
                result.add(matrix[top][column]);
            }

            // 2.右边列——从上到下，行row在变，边界为top+1到bottom
            for (int row = top + 1; row <= bottom; row++) {
                result.add(matrix[row][right]);
            }

            /*
             * 如果只有一行(top == bottom)或者一列(left == right)，前两步则已经完成遍历
             * 否则，底部行——从右往左遍历；左边列——从下往上遍历
             */
            if (top < bottom && left < right) {
                // 3.底部行——从右往左遍历：列column在变，边界为right-1到left
                for (int column = right - 1; column >= left; column--) {
                    result.add(matrix[bottom][column]);
                }

                // 4.左边列——从下往上遍历，行row在变，边界为bottom-1到top
                for (int row = bottom - 1; row > top; row--) {
                    result.add(matrix[row][left]);
                }
            }

            // 5.一层遍历结束，准备遍历下一层，先定位
            left++;
            right--;
            top++;
            bottom--;
        }
        return result;
    }
}

复杂度分析

时间复杂度：\(O(mn)\)，其中\(m\)和\(n\)分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。

空间复杂度：\(O(1)\)，除了输出数组以外，空间复杂度是常数。