算法第二章上机实践报告

1.实践题目名称：

       最大子列和问题

 

2.问题描述：

　　

　　给定K个整数组成的序列{ N​1​​, N​2​​, ..., N​K​​ }，“连续子列”被定义为{ N​i​​, N​i+1​​, ..., N​j​​ }，其中 1。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

　　本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

              数据1：与样例等价，测试基本正确性；

              数据2：102个随机整数；

              数据3：103个随机整数；

              数据4：104个随机整数；

              数据5：105个随机整数；

 

3.算法描述：

　　将给定序列一分为二，分为左右两个子序列，从中间元素向左边开始查找左端最大子序列和，向右边开始查找右端最大子序列和，在与横跨中间元素的最大子序列和做比较，得出整个序列的最大子列和。

 

4.代码：

 

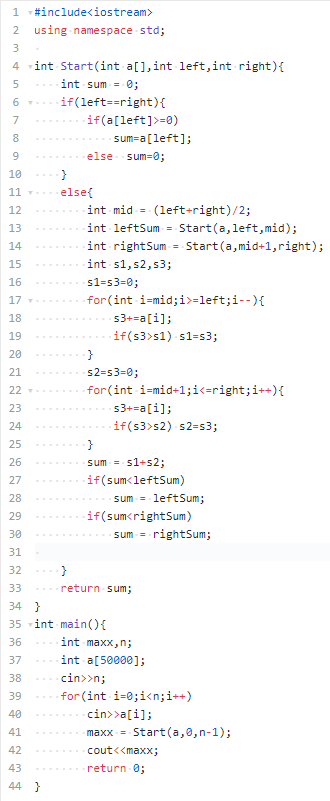
5.算法时间复杂度分析：

       首先要把问题从中间一分为二进行递归，时间复杂度为O(logn)    再进行子段求和为O(n)，最终时间复杂度为O(nlogn)

6.心得:

       一开始用暴力解，写起来是很快，但是分治递归提供了一种新的思路，从中间开始，让解决问题的思路更多，以后找到类似这种的有规律的题尽量用分治法来尝试一下