简单谈谈栈
一、前言
计算机程序离不开算法和数据结构,数据结构这门学科就是为了让计算机能够以更加高效,简单,便捷的方式来存储和使用数据而产生的。本文简单介绍栈(Stack)和队列(Queue)的实现
二、图解

三、线性表
1、 顺序存储结构:用一段地址连续的存储单元依次存储线性表的数据元素
2、 链式存储结构:用一组任意的存储单元存储线性表的数据元素,这组存储单元可以连续,也可以不连续,空间与内存没有线性关系
四、栈
栈
1、只允许在一端进行插入和删除操作的线性表
2、 实现的功能
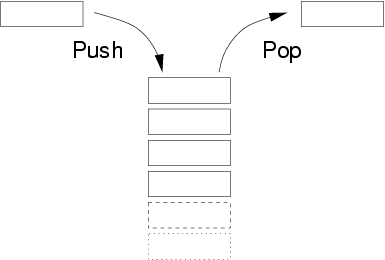
- push:在最顶层加入数据。
- pop:返回并移除最顶层的数据。
- peek:返回最顶层数据的值,但不移除它。
- empty:返回一个布尔值,表示当前stack是否为空栈。
2-1、初始化
private int[] arr;
//常量用大写
private final static int SIZE = 1;
//栈的当前指针
private int index;
//构造器没有参数的
public StackDemo() {
arr = new int[SIZE];
index = -1;
}
2-2、push
//入栈
private void push(int target){
if (index == SIZE){
throw new StackOverflowError();
}else {
//刚开始为-1,要前加
arr[++index] = target;
}
}
2-3、peek
//返回栈顶元素
private int peek(){
if (index == -1){
throw new StackOverflowError();
}else {
return arr[index];
}
}
2-4、empty
//判空
private boolean empty(){
if (index == -1){
return true;
}
return false;
}
3、代码实现
import java.util.Arrays;
/**
*
* @author buer
* @date 2019/1/20
*/
public class StackDemo {
private int[] arr;
//常量用大写
private final static int SIZE = 1;
//栈的当前指针
private int index;
//构造器没有参数的
public StackDemo() {
arr = new int[SIZE];
index = -1;
}
//入栈
private void push(int target){
if (index == SIZE){
throw new StackOverflowError();
}else {
//刚开始为-1,要前加
arr[++index] = target;
}
}
//出栈
private int pop(){
if (index == -1){
throw new StackOverflowError();
}else {
return arr[index--];
}
}
//返回栈顶元素
private int peek(){
if (index == -1){
throw new StackOverflowError();
}else {
return arr[index];
}
}
//判空
private boolean empty(){
if (index == -1){
return true;
}
return false;
}
public static void main(String[] args) {
StackDemo stackDemo = new StackDemo();
stackDemo.push(1);
System.out.println(stackDemo.toString());
stackDemo.pop();
System.out.println(stackDemo.toString());
}
@Override
public String toString() {
return "StackDemo{" +
"arr=" + Arrays.toString(arr) +
", index=" + index +
'}';
}
}
应用
1、括号匹配
2、中缀表达式(人类的思考)和后缀表达式(计算机的计算)
3、递归
4、浏览器的前进后退功能
参考资料
https://zh.wikipedia.org
https://www.zhihu.com/question/21318658
http://www.ruanyifeng.com/blog/2013/11/stack.html


