深度学习中的激活函数（activation function）

目录

• 1. 背景
• 2. 深度学习中常见的激活函数
  • 2.1 Sigmoid函数
    • 2.1.1 Gradient Vanishing
    • 2.1.2 输出不是zero-centered
    • 2.1.3 幂运算相对耗时
  • 2.2 tanh函数
  • 2.3 ReLU函数
  • 2.4 Leaky ReLu函数
  • 2.5 ELU（Exponential Linear Units）函数
  • 2.6 Mish函数
  • 2.7 Exponential激活函数
  • 2.8 Softsign函数
  • 2.9 Softplus函数
  • 2.10 Swith函数
• 3. 小结
• Reference

下文中相关的程序见：Github: DeepLearning/activations

1. 背景

  深度学习的基本原理是基于人工神经网络，信号从一个神经元进入，经过no-linear activation function，传入到下一层神经元；再经过该层神经元的activate，继续往下传递，如此循环往复，直到输出层。正是由于这些非线性函数的反复叠加，才使得神经网络有足够的capacity来抓取复杂的pattern，再各个领域取得state-of-the-art的结果。显而易见，activate function在深度学习中举足轻重，也是很活跃的研究领域之一。目前来讲，选择怎样的activation function不在于它能否模拟真正的神经元，而是在于能够便于优化整个神经网络。下面我们简单聊一下各类函数的特点以及为什么现在优先推荐ReLU函数。

2. 深度学习中常见的激活函数

2.1 Sigmoid函数

前向：

\[\sigma = \dfrac{1}{1+e^{-x}} \]

后向：

\[\dfrac{\partial \sigma}{\partial x} = \sigma \cdot (1- \sigma) \]

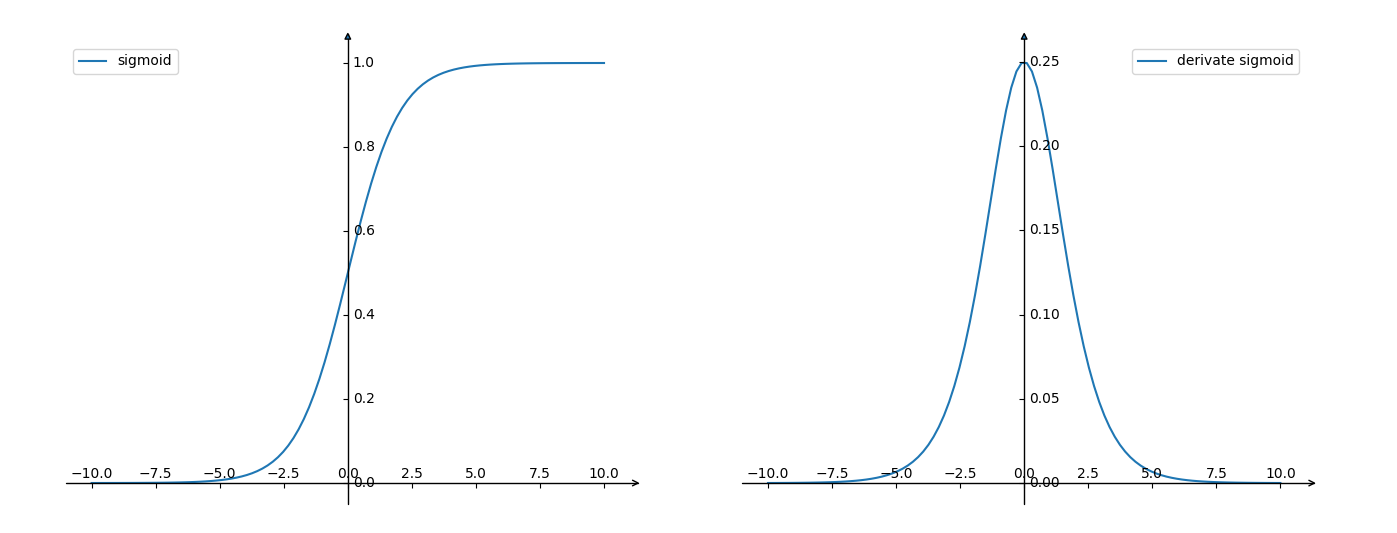
  Sigmoid函数是深度学习领域开始时使用频率较高的activation function。它是便于求导的平滑函数，其导数为\(\sigma(x)(1-\sigma(x))\)，这是优点。然而，Sigma有三大缺点：

• 容易出现gradient vanishing
• 函数输出并不是zero-centered
• 幂运算相对来讲比较耗时

2.1.1 Gradient Vanishing

  优化神经网络的方法是Back Propagation，即导数的后向传递：先计算输出层对应的loss，然后将loss以导数的形式不断向上一层网络传递，修正相应的参数，达到降低loss的目的。Sigmoid函数在深度网络中常常会导致导数逐渐变为0，使得参数无法被更新，神经网络无法被优化。原因在于两点：

（1）在上图中容易看出，\(\sigma(x)\)中\(x\)较大或较小时，导数接近于0，而后向传递的数学依据时微积分求导的链式法则，当前层的导数需要之前各层导数的乘积，几个小数的相乘，结果会很接近于0；

（2）Sigmoid导数的最大值时0.25，这意味着导数在每一层至少会被压缩为原来的1/4，通过两层后被变为1/16，...，通过10层后为1/1048576。请注意这里时“至少”，导数达到最大值这种情况还是很少见的。

2.1.2 输出不是zero-centered

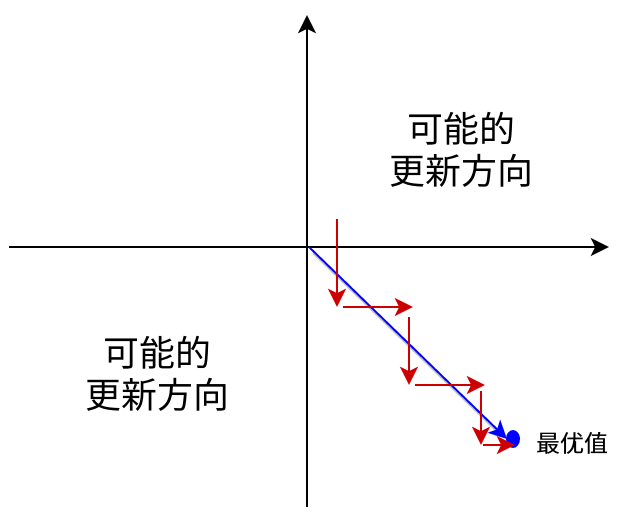
  Sigmoid函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。举例来讲，对\(\sigma(\sum_iw_ix_i+b)\)，如果所有\(x_i\)均为正数或负数，那么其对\(w_i\)的导数总是正数或负数，这会导致如下图红色箭头所示的阶梯式更新，这显然并非一个好的优化路径。深度学习往往需要大量时间来处理大量数据，模型的收敛速度时尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据（可以通过数据预处理实现）和zero-centered输出。

2.1.3 幂运算相对耗时

相对于前两项，这其实并不是一个大问题，我们目前是具备相应计算能力的，但面对深度学习中庞大的计算量，最好能省则省 😃。之后我们会看到，在ReLu函数中，需要做的仅仅是一个thresholding，相对幂运算来讲会快很多。

2.2 tanh函数

tanh是双曲函数中的一个，称为双曲正切函数；

前向：

\[tanh(x) = \dfrac{e^x-e^{-x}}{e^x+e^{-x}} \]

后向：

\[\dfrac{\partial tanh}{\partial x} = 1 - (tanh)^2 \]

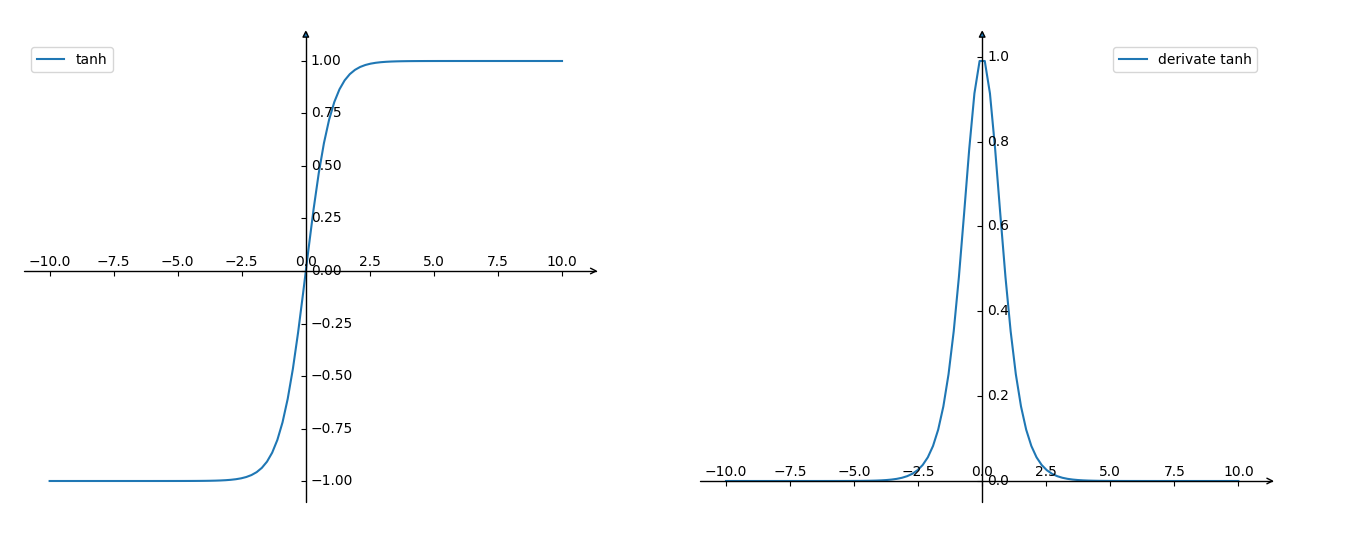
如上图所示，它解决了zero-centered的输出问题，然而，gradient vanishing的问题和幂运算的问题仍然存在。

2.3 ReLU函数

\[ReLU = max(0, x) \]

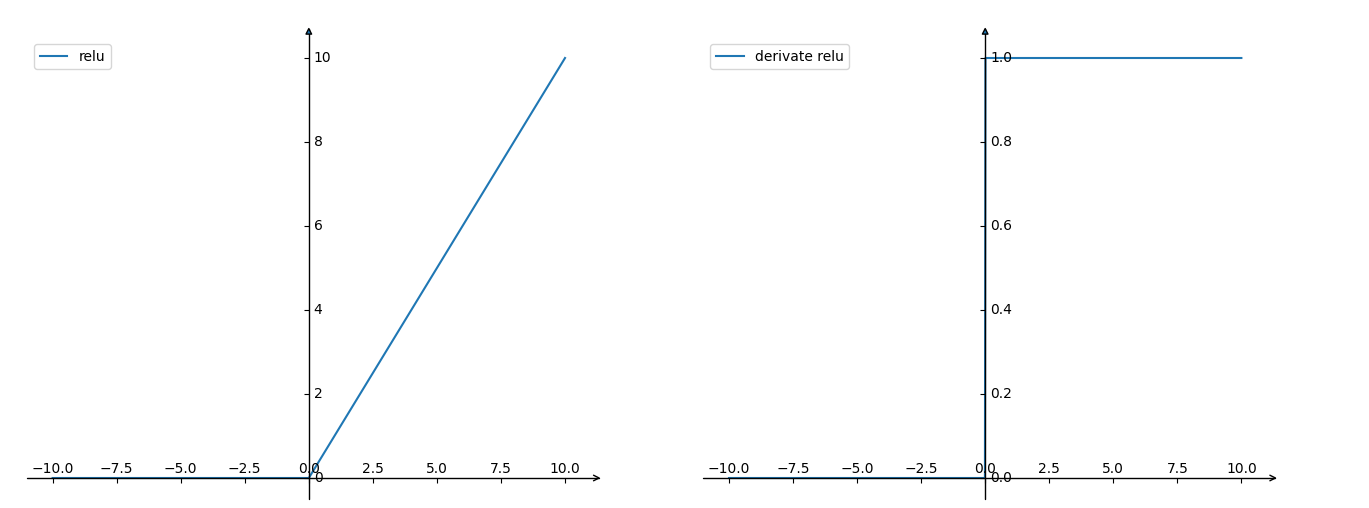
  ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。ReLU虽然简单，但是确实近几年的重要成果，有以下几大优点：

• 解决了gradient vanishing的问题（在正区间）
• 计算速度非常快，只需要判断输入是否大于0
• 收敛速度快于Sigmoid和tanh

ReLU也有几个需要特别注意的问题：

（1）ReLU的输出不是zero-centered

（2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生：

• 非常不幸的参数初始化，这种情况比较少见；
• learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法；

尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试；

2.4 Leaky ReLu函数

Leaky Relu激活函数与ReLu类似，不同点仅仅在于负数阶段上，Leaky ReLU给负值赋予一个非零的斜率；

前向：

\[\begin{equation} f(x)=\left\{ \begin{aligned} x & & if \quad x \ge 0 \\ \alpha \cdot y & & if \quad x < 0 \\ \end{aligned} \right. \end{equation} \]

反向：

\[\begin{equation} \dfrac{\partial f(x)}{\partial x}=\left\{ \begin{aligned} 1 & & if \quad x \ge 0 \\ \alpha & & if \quad x < 0 \\ \end{aligned} \right. \end{equation} \]

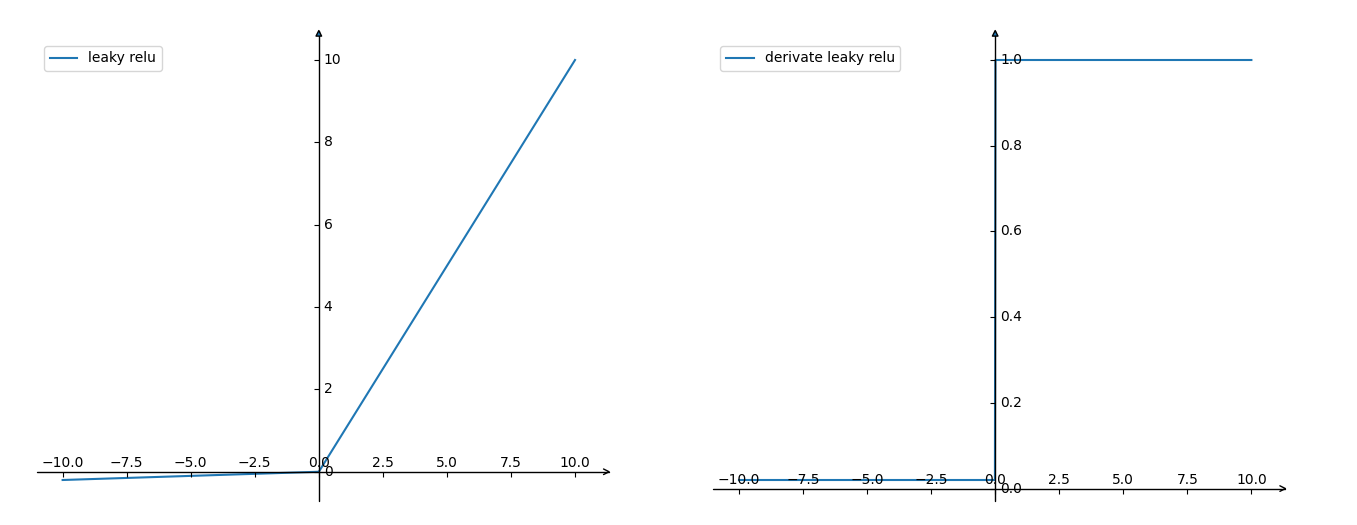
人们为了解决Dead ReLU Problem，提出了将ReLU的前半段设为\(0.02x\)而非0。

理论上来讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

2.5 ELU（Exponential Linear Units）函数

前向：

\[f(x)=\begin{cases}x, &if\ x \ge 0 \cr\alpha(e^x-1), & if\ x < 0 \end{cases} \]

后向：

\[f(x)=\begin{cases}1, &if\ x \ge 0 \cr\alpha \cdot e^x, & if\ x < 0 \end{cases} \]

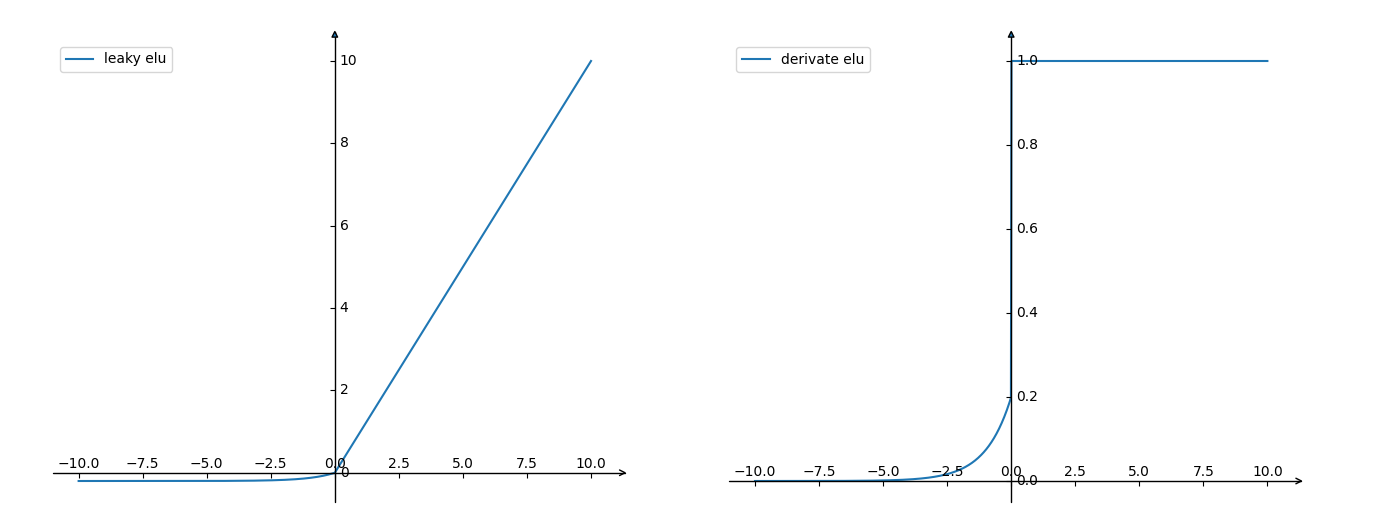
ELU也是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点，以及：

• 不会有Dead ReLU问题
• 输出的均值接近于0，zero-centered

它的一个小问题在于计算量稍大。类似于Leaky ReLU，理论上虽然好于ReLU，但在实际使用中目前并没有好的证据ELU总是优于ReLU。

2.6 Mish函数

Mish激活函数是光滑的非单调激活函数：

前向：

\[f(x) = x \cdot tanh(ln(1+e^x)) \]

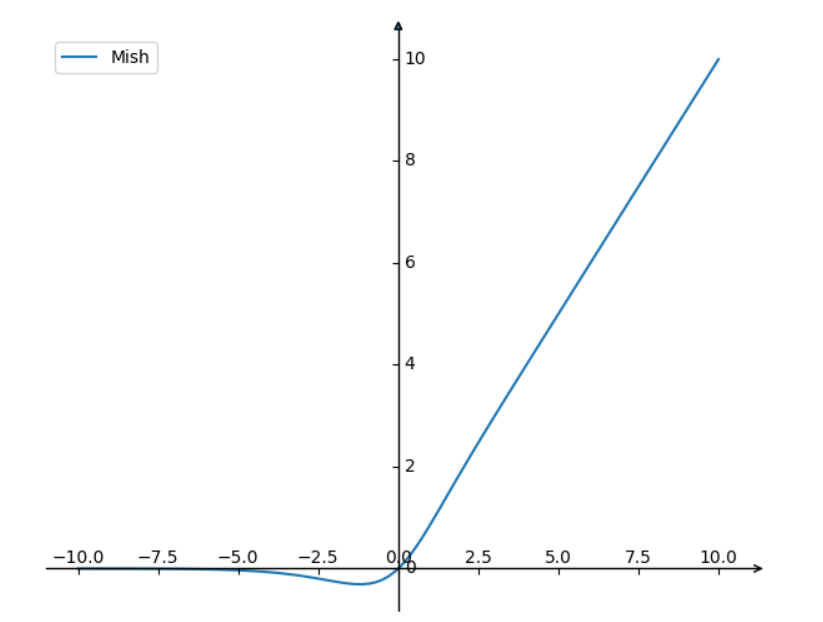
Mish激活函数的功能：

1. 无上界，有下界：无上界是任何函数都需要具备的特性，因为它避免了导致训练速度急剧下降的梯度饱和；因此，加快训练过程；无下届属性有助于实现强正则化效果；
2. 非单调函数：有助于保持小的负值，从而稳定网络梯度流；
3. 无穷连续性和光滑性：Mish是光滑函数，具有较好的泛化能力和结果的有效优化能力，可以提高结果的质量；
4. 计算量较大，但是效果好：与ReLU相比，它的计算量比较大，但是深度神经网络中显示了比ReLU更好的结果。
5. 自门控：

2.7 Exponential激活函数

前向：

\[f(x) = e^x \]

后向：

\[\dfrac{\partial f(x)}{\partial x} = e^x \]

没啥区别；

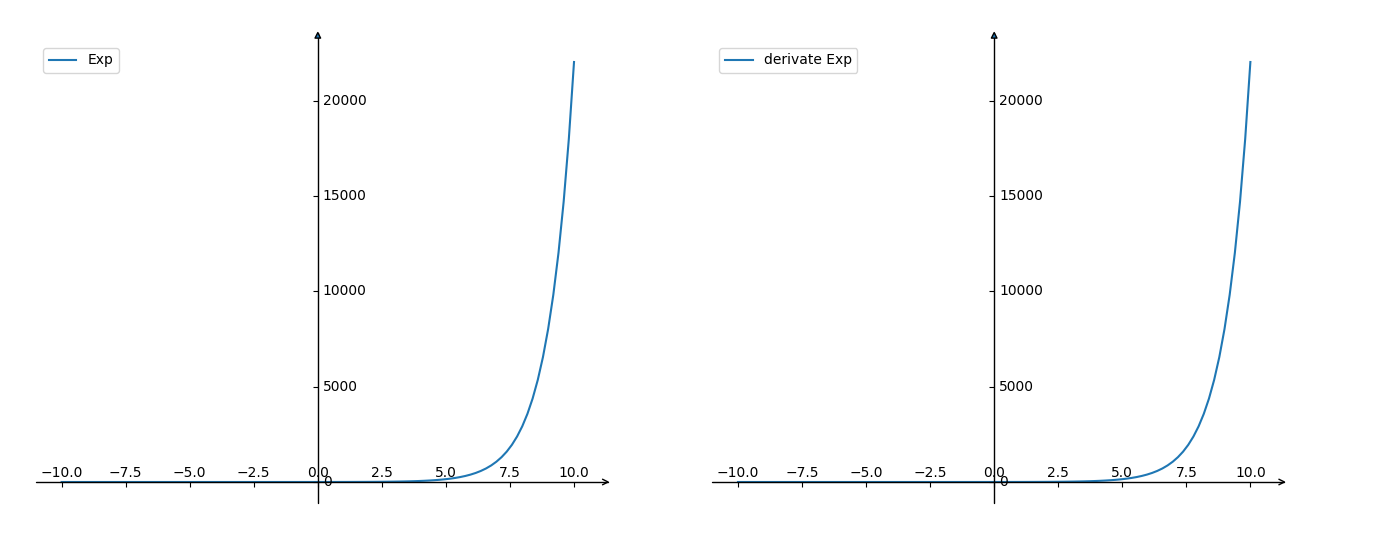
说明：

• 从这个图上，看这个指数根本不太适合用于激活函数啊，毕竟是指数级，增长的也太快了；
• 之所以加上这个，是因为TensorFlow中提供了这个激活函数；

2.8 Softsign函数

前向：

\[f(x) = \dfrac{x}{|x|+1} \]

反向：

\[\dfrac{\partial f(x)}{\partial x} = \dfrac{1}{(1+|x|)^2} \]

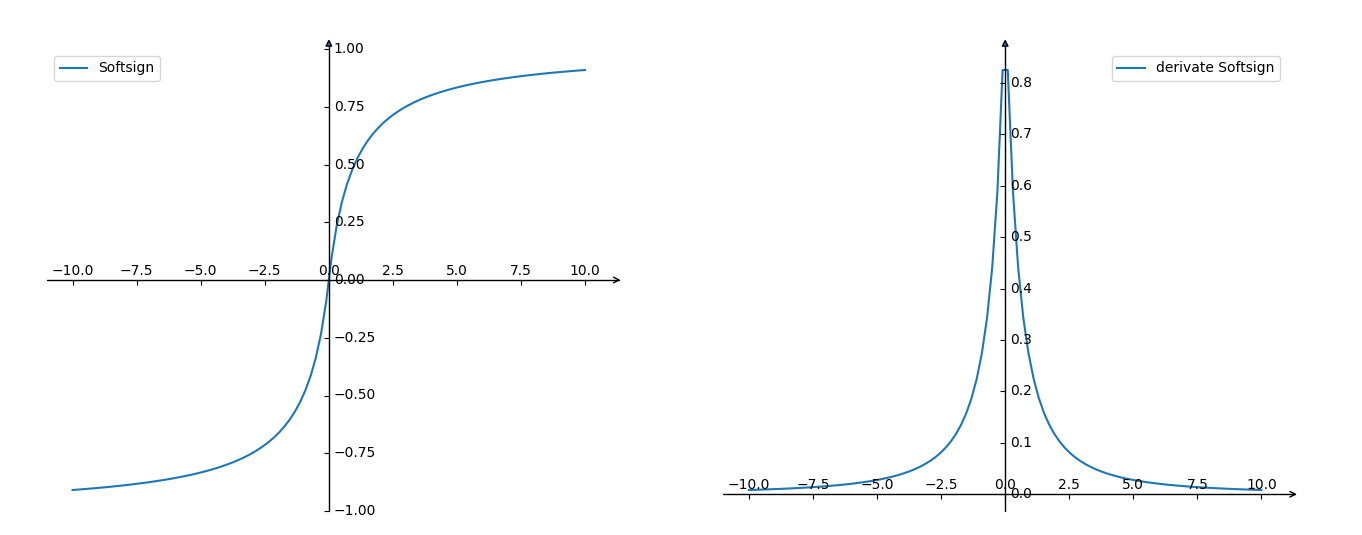
2.9 Softplus函数

前向：

\[f(x)= log(1+e^x) \]

后向：

\[\dfrac{\partial f(x)}{\partial x} = \dfrac{e^x}{1+e^x} \]

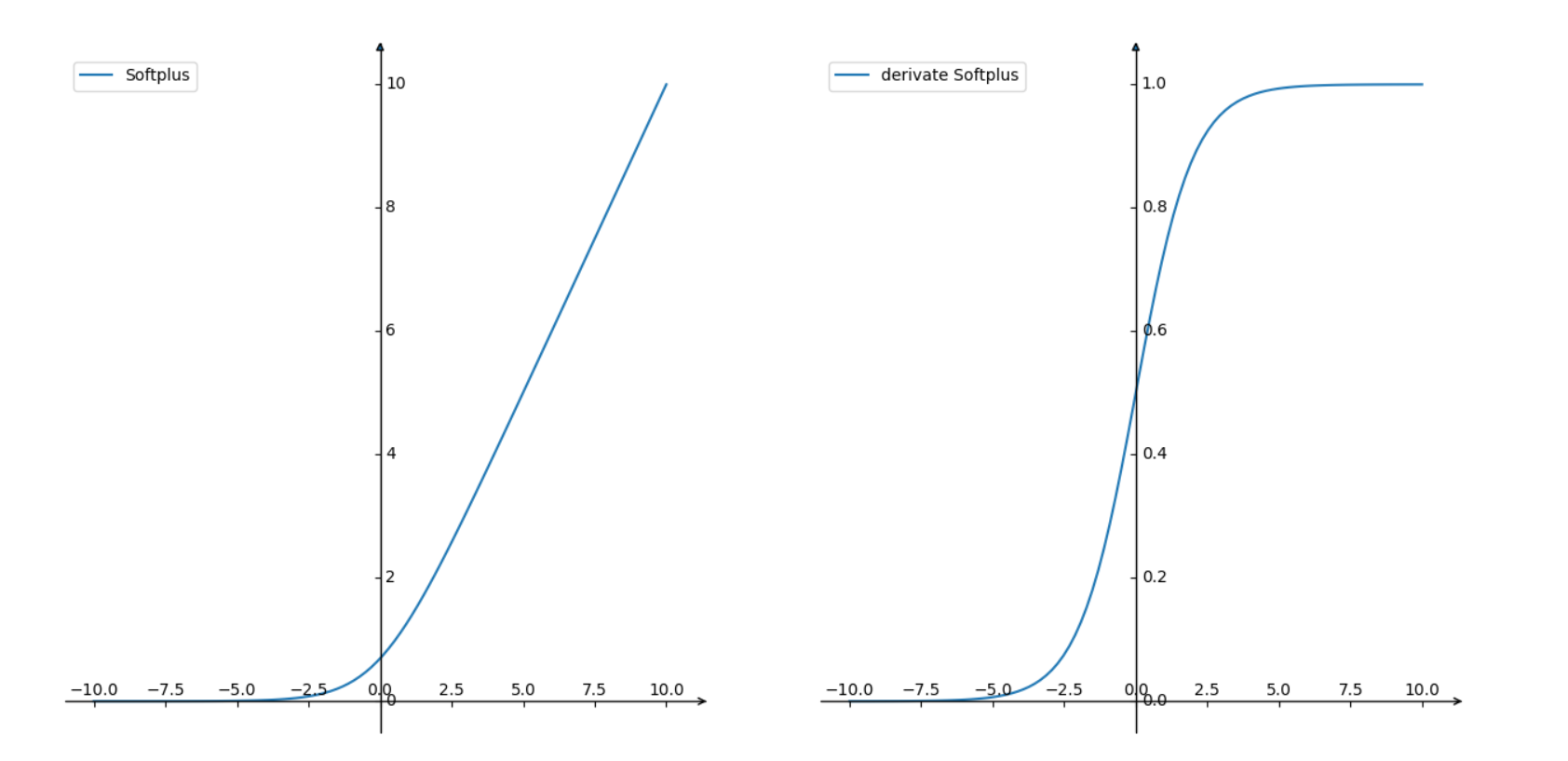
2.10 Swith函数

前向：

\[f(x) = x \cdot sigmoid(x) \]

后向：

\[\dfrac{\partial f(x)}{\partial x} = \dfrac{1-x+2e^{-x}}{(1+e^{-x})^2} \]

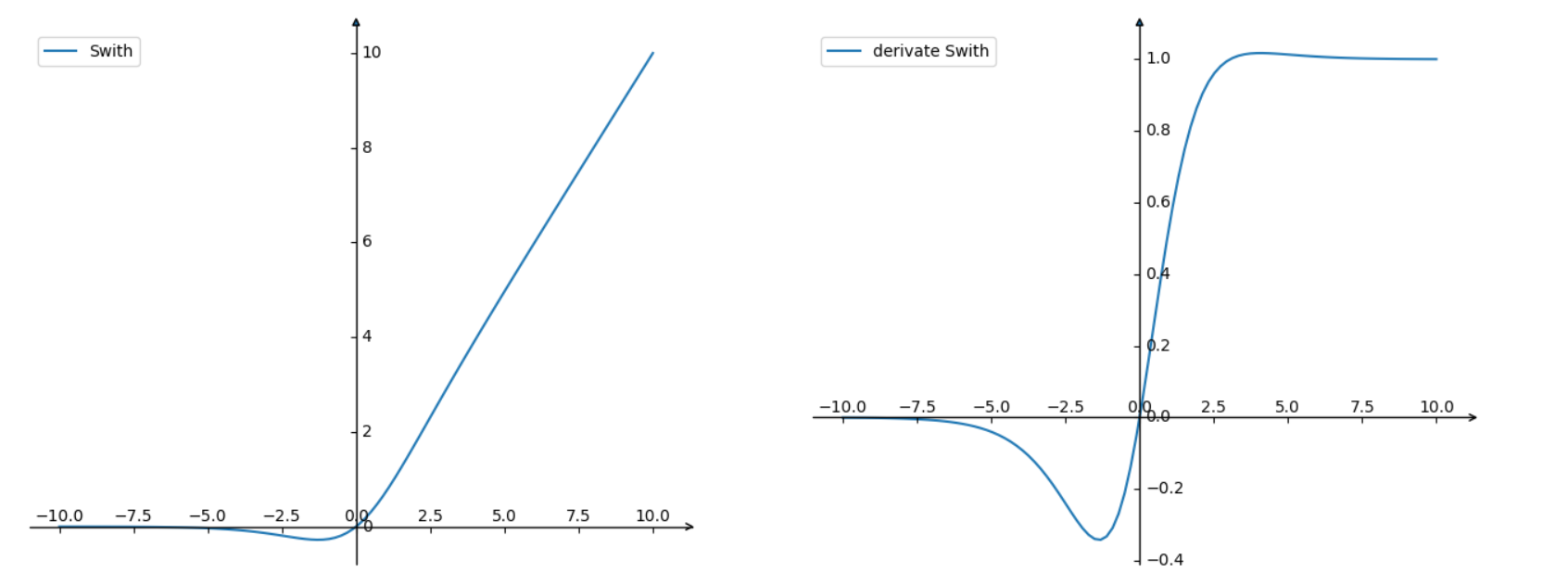
3. 小结

  建议使用ReLU函数，但是要注意初始化和learning rate的设置；可以尝试用Leaky ReLU或ELU函数；不建议使用tanh，尤其是Sigmoid函数；

另外，选用激活函数的时候主要关注以下几点：

• 是否容易引起梯度消失；
• 输出是否是zero-centered；
• 是否包含复杂的运算；
• 是否容易求导；

Reference

• Udacity Deep Learning Courses
• Stanford CS231n Course
• 夏飞-聊一聊深度学习的activation function
• 神经网络中的激活函数的作用和选择
• 【python实现卷积神经网络】激活函数的实现（sigmoid、softmax、tanh、relu、leakyrelu、elu、selu、softplus）