bzoj2687: 交与并

Description

    对于一个区间集合{A1,A2……AK}(K>1，Ai<>Aj{i<>j})，我们定义其权值
           W=|A1∪A2∪……∪AK|*|A1∩A2∩……AK|

     当然，如果这些区间没有交集则权值为0。

 

Input

    给你N个各不相同的区间，请你从中找出若干个区间使其权值最大。

 

 第一行N

 接下来N行 l r(1<=l<r<=10^6)

Output

    最大权值

Sample Input

4

1 6

4 8

2 7

3 5

Sample Output

24


样例注释:选择第1个和第3个区间,交为(2,6),并为(1,7),
权值为4*6=24.

HINT

 

100%  1<N<=10^6

题解：

选出的最优区间集合满足下列性质：

1.交集肯定不能为空。

2.设这个区间集合的并集为U，对于任意一个区间，设这个区间集合去掉这个区间的并集为U'，满足U'⫋U。

第一条显然。。。

第二条：假如去掉这个集合后并集没有减小，去掉后显然交集不会减小，所以答案也不会变小。

所以选出来的集合只有一个区间或两个互不包含的区间。

由于集合大小不能为1，所以只能选两个区间。

首先我们将区间按左端点从小到大，如果左端点相同，则按右端点从大到小的顺序排好序。

对于其中一个区间含于另一个区间的情况：显然包含它的区间只能在他前面，而且具有单调性，所以用个单调队列维护一下即可。

对于两个互不包含的区间的情况：先将含于其他区间的区间去掉，这时区间的左右端点都单调上升，然后有一个性质：

假如第i-1个区间选择的最优区间为第k个（k<i-1），第i个区间选择的最优区间为第j个（j<i），则有k<=j

证明：

假设j<k，对于i，有：

 

同理，对于i-1（记作i'），有：

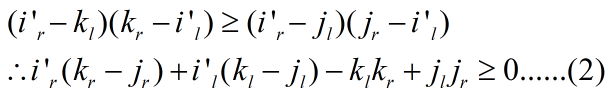
所以假设不成立，所以有k<=j，这样就有决策单调性了，用栈来维护一下即可。

code:

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
char ch;
bool ok;
void read(int &x){
    for (ok=0,ch=getchar();!isdigit(ch);ch=getchar()) if (ch=='-') ok=1;
    for (x=0;isdigit(ch);x=x*10+ch-'0',ch=getchar());
    if (ok) x=-x;
}
const int maxn=1000005;
typedef long long int64;
int n,cnt,last;
int64 ans;
struct Seg{
    int l,r;
}seg[maxn];
inline bool cmp(const Seg &a,const Seg &b){return (a.l<b.l)||(a.l==b.l&&a.r>b.r);}
inline int64 calc(const Seg &j,const Seg &i){return 1LL*(i.r-j.l)*(j.r-i.l);}
struct Stack{
    int top,pos;
    struct Data{
        int l,r,id;
    }s[maxn],tmp;
    void init(){s[top=1]=(Data){2,n,1},pos=1;}
    bool cmp(int a,int x,int y){return calc(seg[x],seg[a])<calc(seg[y],seg[a]);}
    int get(int id){
        int l=tmp.l,r=tmp.r,m,a=tmp.id;
        while (l<r){
            m=((l+r)>>1)+1;
            if (cmp(m,a,id)) l=m; else r=m-1;
        }
        return l;
    }
    void push(int id){
        while (top&&!cmp(s[top].l,s[top].id,id)) top--;
        tmp=s[top--];
        int m=get(id);
        if (tmp.l<=m) s[++top]=(Data){tmp.l,m,tmp.id};
        if (m<n) s[++top]=(Data){m+1,n,id};
    }
    int64 query(int x){
        while (x>s[pos].r) pos++;
        return calc(seg[s[pos].id],seg[x]);
    }
}stack;
struct Que{
    int head,tail;
    struct Data{
        int r,len;
    }q[maxn],tmp;
    void init(){head=1,tail=0;}
    void push(int id){
        tmp=(Data){seg[id].r,seg[id].r-seg[id].l};
        while (head<=tail&&q[tail].len<=tmp.len) tail--;
        q[++tail]=tmp;
    }
    int64 query(int id){
        int r=seg[id].r;
        while (head<=tail&&q[head].r<r) head++;
        if (head<=tail) return q[head].len;
        else return -1;
    }
}que;
int main(){
    read(n);
    for (int i=1;i<=n;i++) read(seg[i].l),read(seg[i].r);
    sort(seg+1,seg+n+1,cmp),que.init();
    for (int i=1;i<=n;i++)
        if (seg[i].r>last) last=seg[i].r,seg[++cnt]=seg[i],que.push(i);
        else ans=max(ans,que.query(i)*(seg[i].r-seg[i].l));
    n=cnt,stack.init();
    for (int i=2;i<=n;i++) ans=max(ans,stack.query(i)),stack.push(i);
    printf("%lld\n",ans);
    return 0;
}