C语言I博客作业11
二、本周作业头
| 这个作业属于那个课程 | C语言程序设计II |
|---|---|
| 这个作业要求在哪里 | https://i-beta.cnblogs.com/posts/edit;postId=11994847 |
| 我在这个课程的目标是 | 学习使用c语言 |
| 这个作业在那个具体方面帮助我实现目标 | 加强对定义函数的使用和理解 |
| 参考文献 | 教材 |
三、本周作业
PTA实验作业
代码互评
学习总结
四、作业格式
1.PTA实验作业

1.1 题目名1
6-1 统计某类完全平方数 (20分)
本题要求实现一个函数,判断任一给定整数N是否满足条件:它是完全平方数,又至少有两位数字相同,如144、676等。
函数接口定义:
int IsTheNumber ( const int N );
其中N是用户传入的参数。如果N满足条件,则该函数必须返回1,否则返回0。
裁判测试程序样例:
include <stdio.h>
include <math.h>
int IsTheNumber ( const int N );
int main()
{
int n1, n2, i, cnt;
scanf("%d %d", &n1, &n2);
cnt = 0;
for ( i=n1; i<=n2; i++ ) {
if ( IsTheNumber(i) )
cnt++;
}
printf("cnt = %d\n", cnt);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
105 500
输出样例:
cnt = 6
1.1.1数据处理
数据表达:定义了i, a[100]来定义大小为一百的浮点型数组。同时用count来计数,j作为却套语句的循环变量,这些数据都为整型变量,
数据处理:
1.1.2实验代码截图
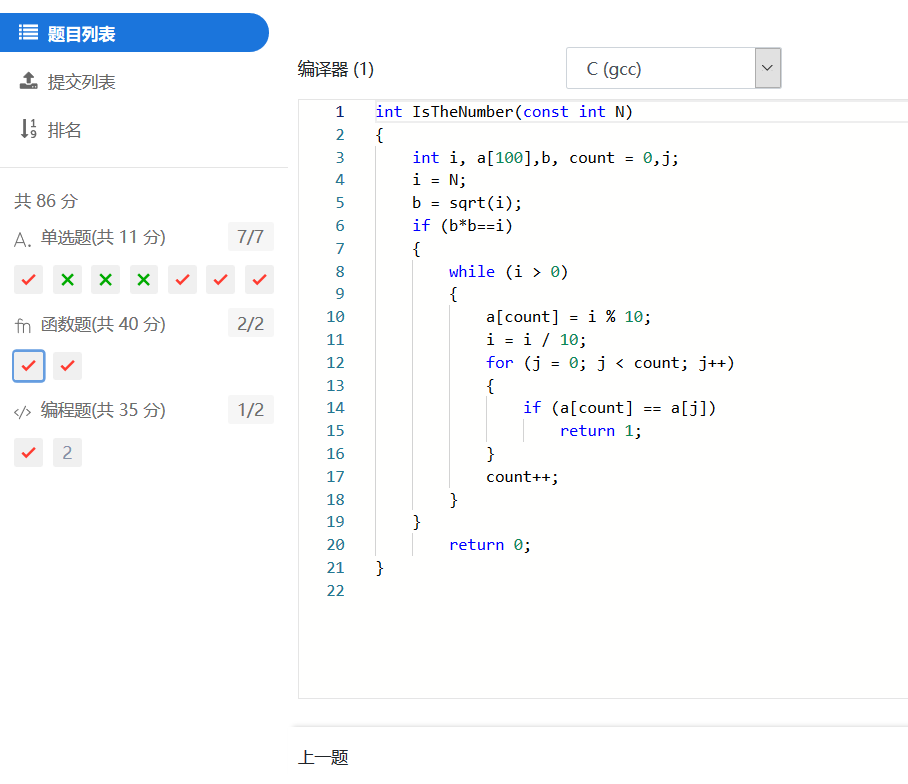
1.1.3 造测试数据
输入数据 |输出数据|
---|---|]
105 500 |cnt = 6|
0 100 | cnt = 1|
500 1000 |cnt = 2|
输出你的程序面向各种测试数据结果,除了题目给出的测试数据,可以自己再造其他临界数据,越多越好,并加上必要说明
1.1.4 PTA提交列表及说明
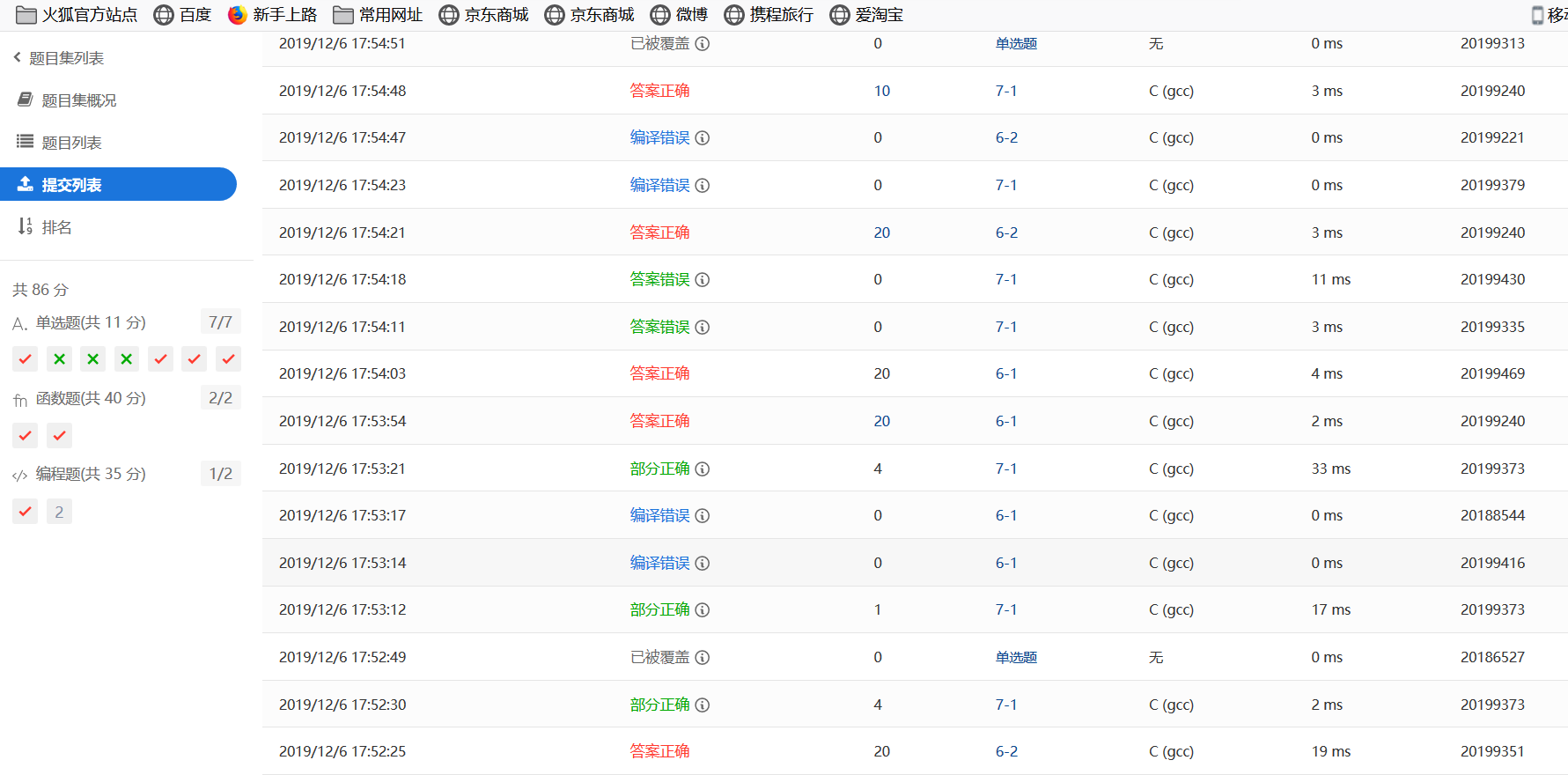
提交列表说明:
在交pta的作业之前,有在C++上面调试过,所以在这里是一次过,但在编写过程中,总会出现编译错误,比如,我把int i;定义成了double i;
而出现后面数据不能计算的错误,
1.2 题目2
7-1 解一元二次方程(*) (10分)
请编写程序,解一元一次方程 ax2+bx+c=0 。
要求:
若a=0,则解一元一次方程。
若方程有唯一解,则输出方程的根;
若方程无解,则输出“无解”;
若方程有无穷多解,则输出“无穷多解”。
若a≠0,则解一元二次方程。
若Δ>0,则输出方程的两个不等的实根;
若Δ=0,则输出方程的两个相等的实根;
若Δ<0,则输出方程的两个共轭的虚根。
所有实数均以%g输出。
输入样例1
0 4.5 -3.6
输出样例1
x = 0.8
输入样例2
0 0 3.6
输出样例2
无解
输入样例3
0 0 0
输出样例3
无穷多解
输入样例4
-2 0.8 -0.06
输出样例4
x1 = 0.1, x2 = 0.3
输入样例5
-3 1.2 -0.12
输出样例5
x1 = x2 = 0.2
输入样例6
-0.2 0.04 -0.01
输出样例6
x1 = 0.1-0.2i, x2 = 0.1+0.2i
提示:注意实数的负零问题和误差问题。
1.2.1 数据处理
数据表达:用双浮点型定义了a b c 三个系数,主要用于后面的判读和计算。x是方程中的未知数,x1和x2是方程的俩个根,因为都是通过计算得到的数据,所以,用double来定义
数据处理:
1.2.2 实验代码截图
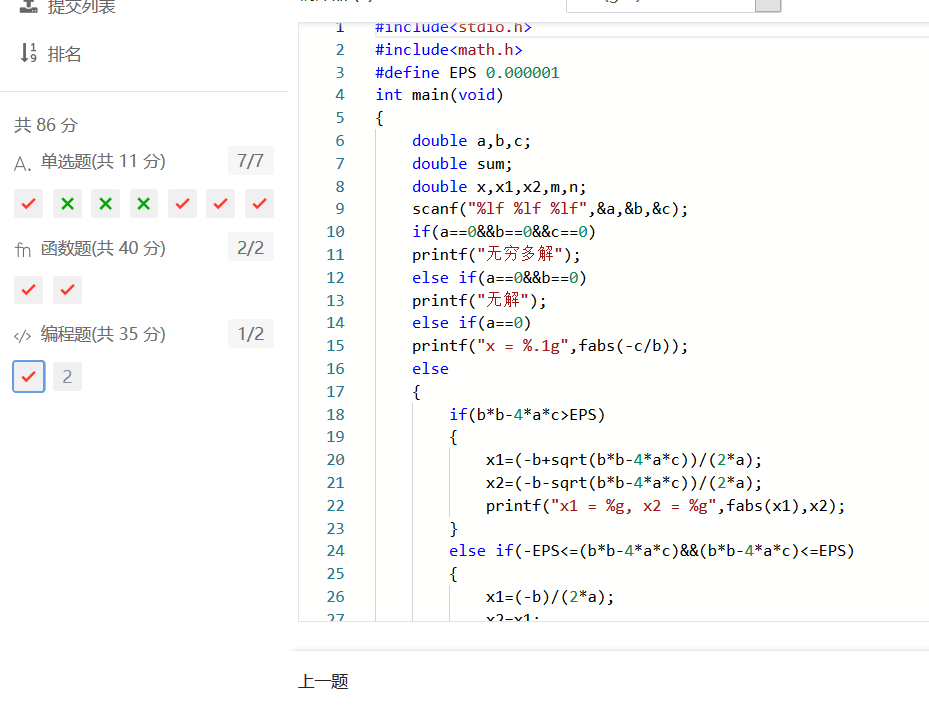
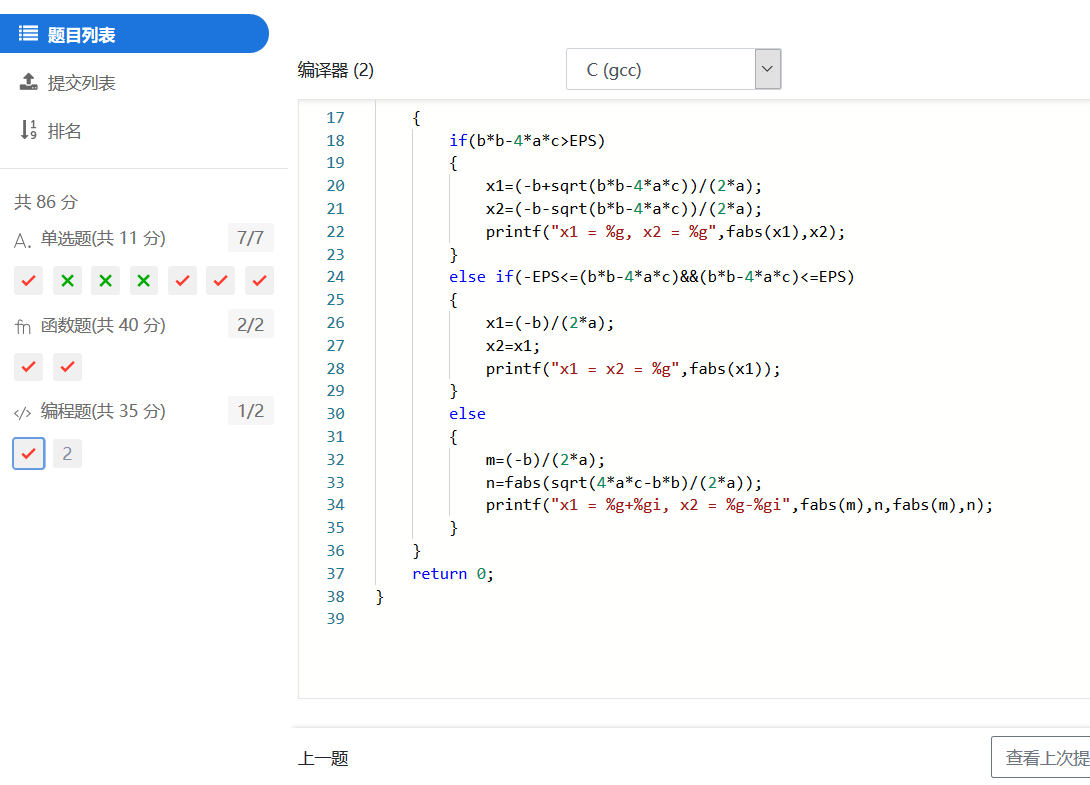
1.2.3 造测试数据
1.2.4 PTA提交列表及说明

说明,在编写这个题目时,开始因为高中知识的原因,一开始总是想着定义一个函数来计算,在输入数据后就直接能算出来,但总是算不正确,定义函数出现错误,后来就直接没有做了,就把整个计算过程拆开,不再定义不同的函数来计算。
2.代码互评(5分)
同学代码截图
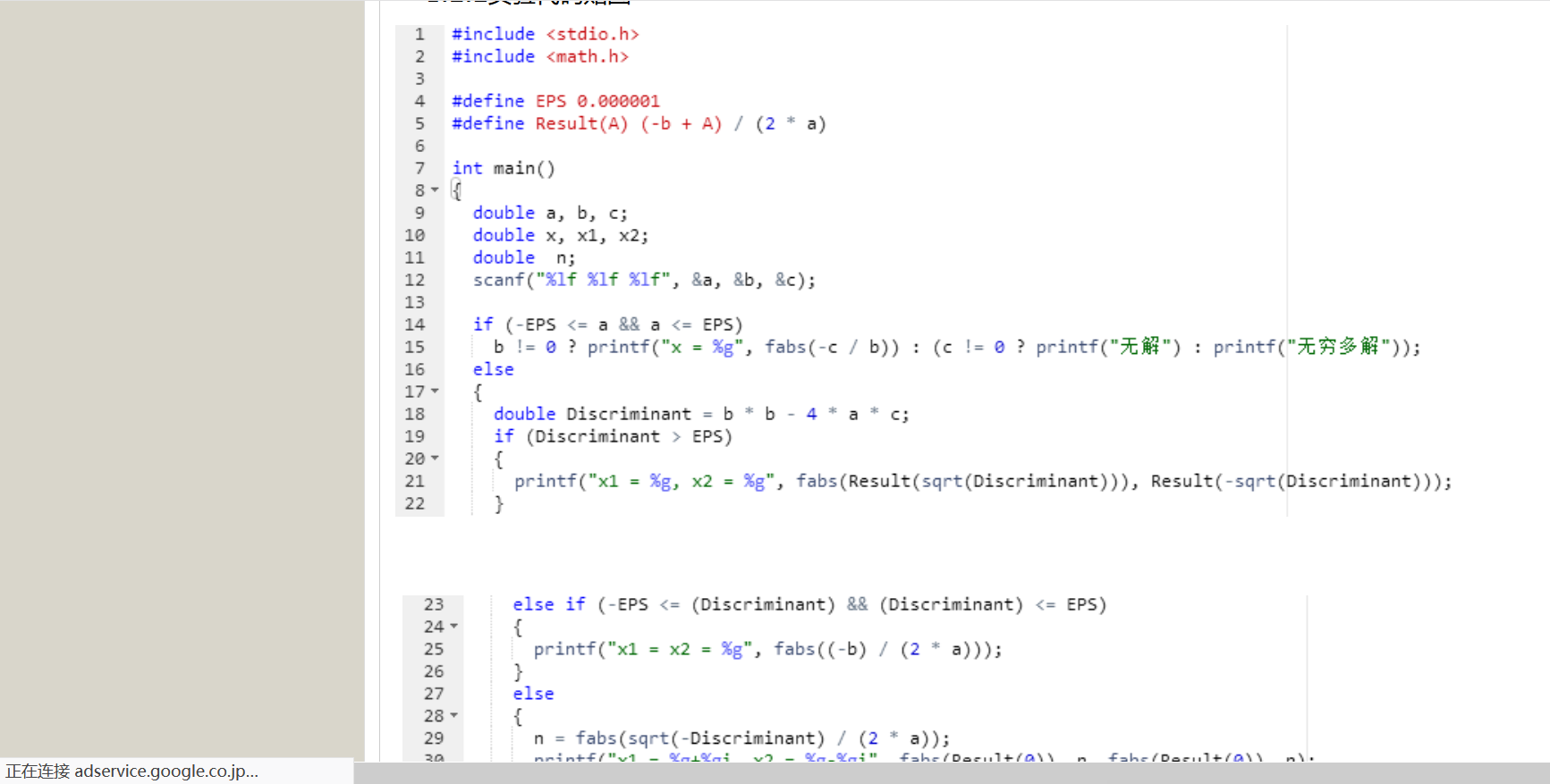
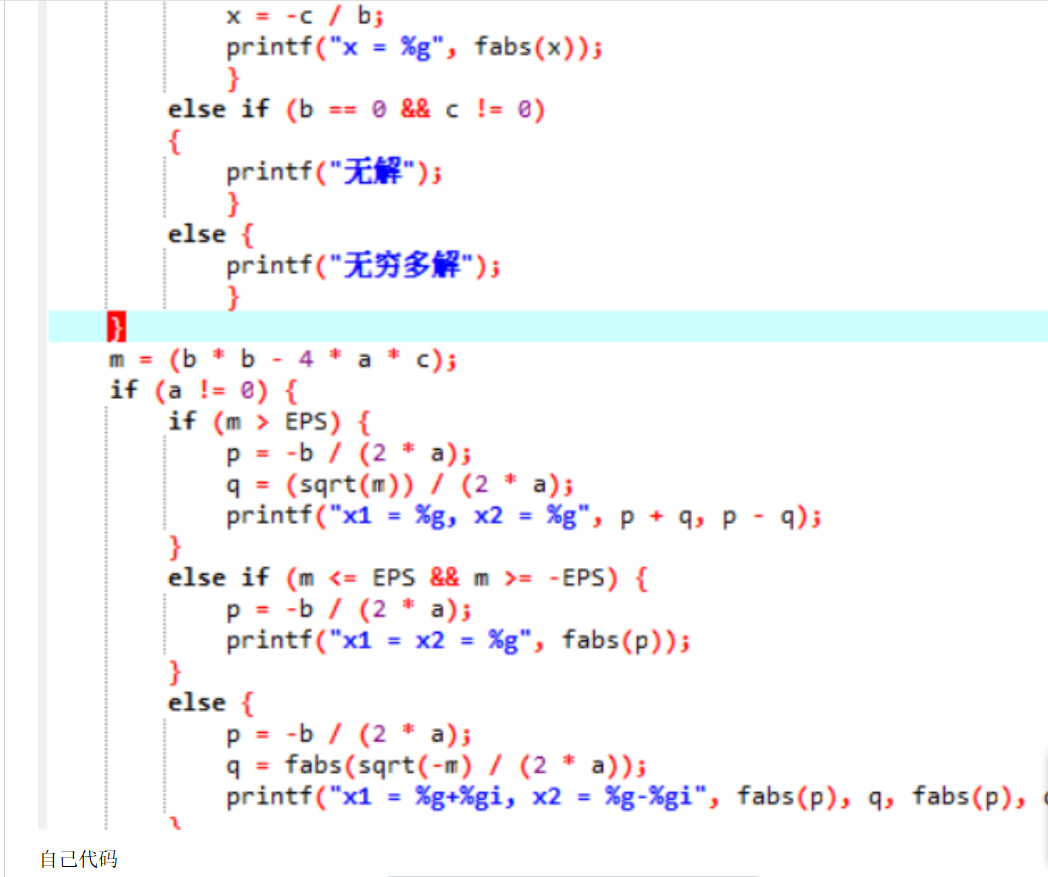
自己代码截图
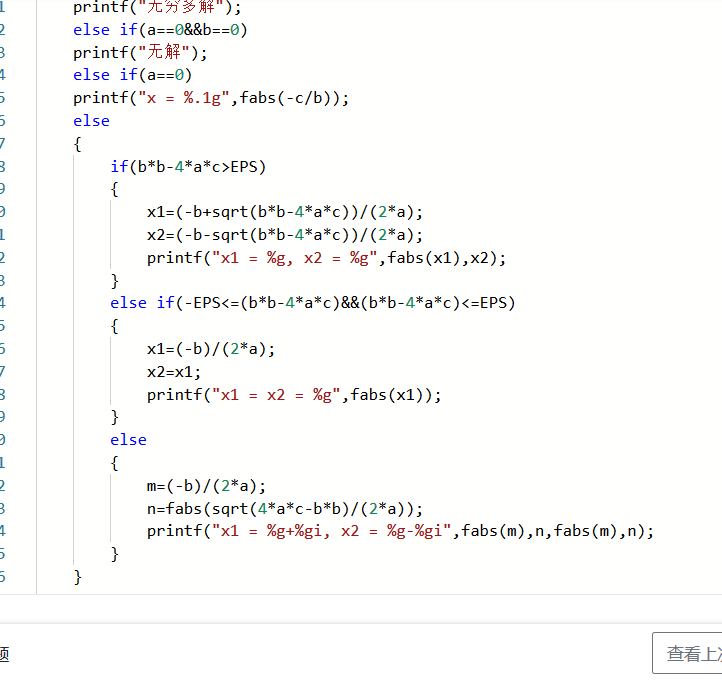
区别:都和相似,但其实不一样
乍一看,
3.学习总结(15分)
3.1 学习进度条(5分)
| 时间 | 写代码所花时间 |
|---|---|
| 四周 | 10 |
| 五周 | 8 |
| 六周 | 8 |
| 七周 | 6 |
| 八周 | 7 |
| 九周 | 5 |
| 十周 | 6 |
3.2 累积代码行和博客字数(5分)
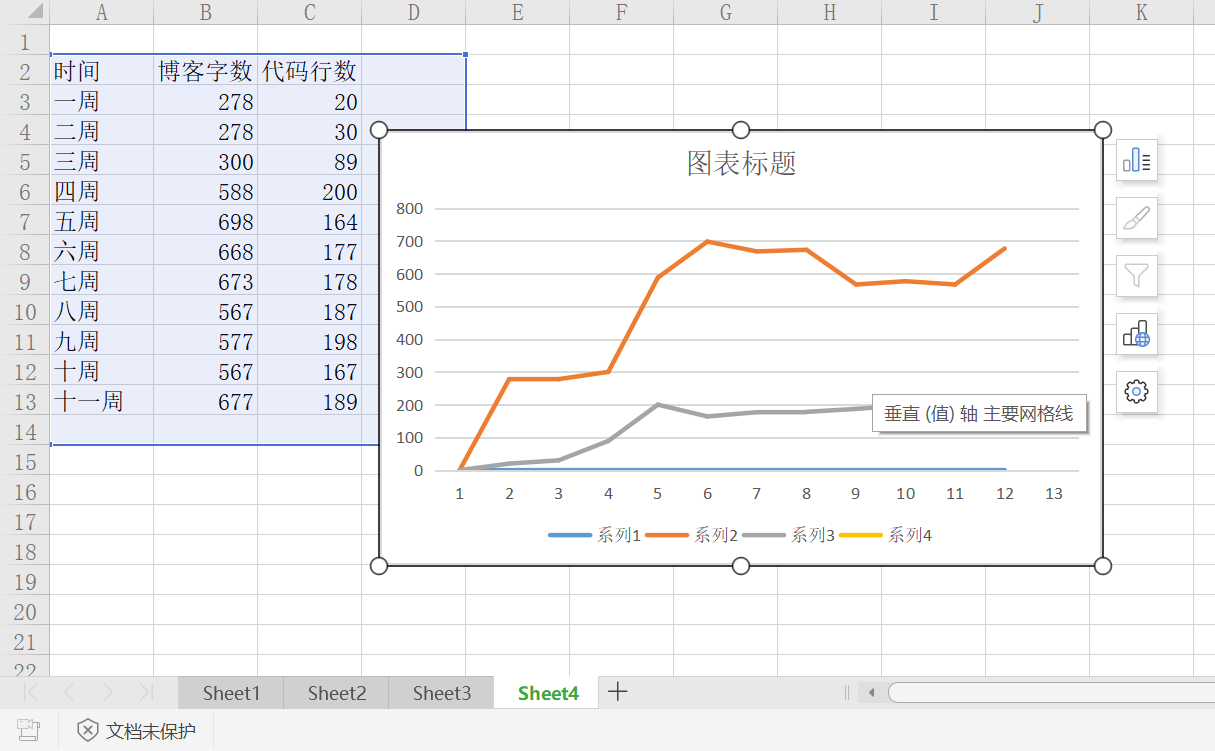
3.3 学习内容总结和感悟(5分)
3.3.1 学习内容总结
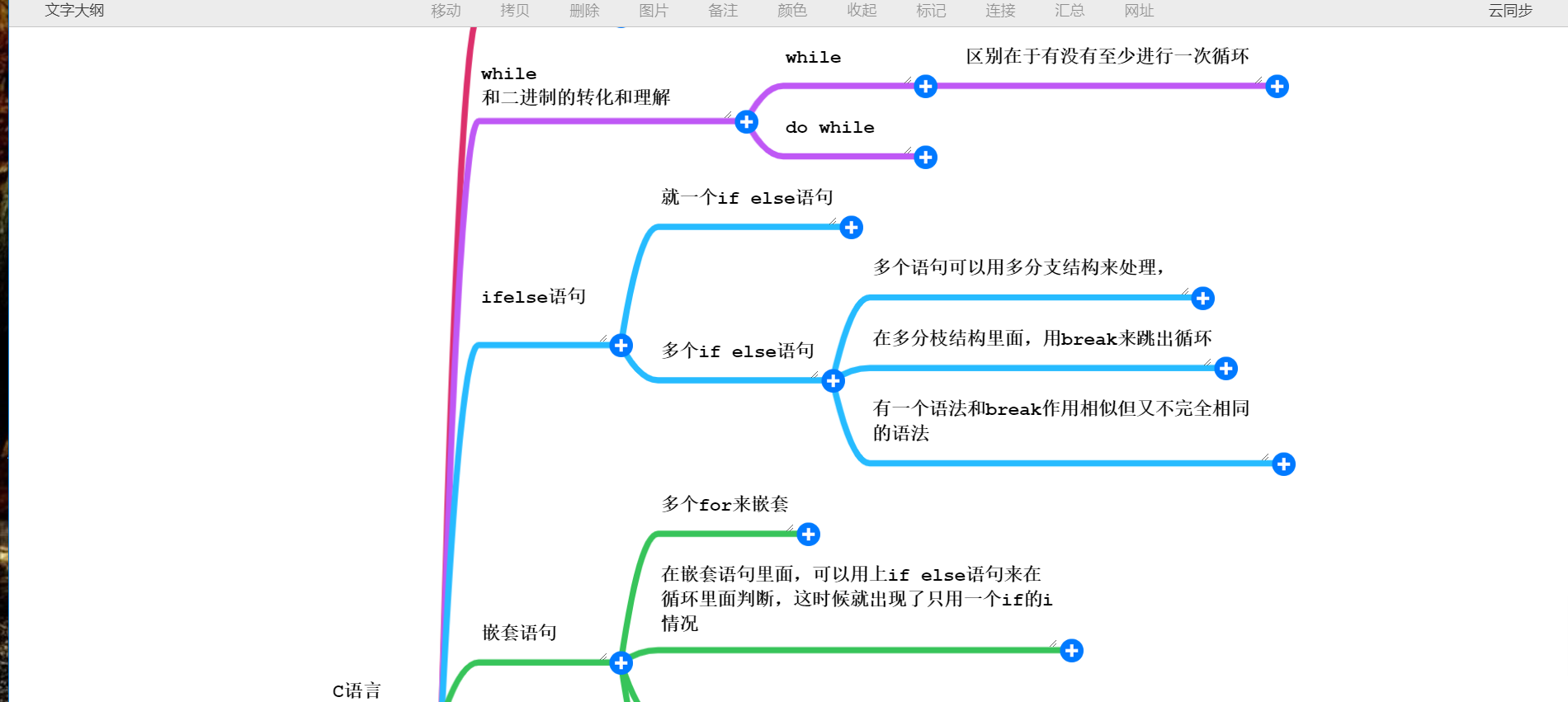
3.3.2 学习体会
从第一次上机课开始,是有一点讨厌调试这个东西的,因为要交作业,还计入平时分,主要啊时候我不会写,只能看着束发带,但现在来说的话,它给了我一种可以判断自己的方式,能很快知道自己有没有错误,还能在知道错误后,进一步知道具体错在哪里,在这次作业中,就有不小的用处,让我的作业看起来美观不少,另外,在定义函数题中,发现自己对这个操纵并不熟悉,还有很大的提升空间。



