「学习笔记」Splay
一.什么是 Splay#
是一种二叉查找树,它通过不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,并且保持平衡,不退化为链。
二.Splay 的结构#
-
二叉查找树的性质#
首先是一颗二叉树。
并且左子树任意节点的值 根节点的值 右子树任意节点的值。 -
节点维护的信息#
根节点编号;
节点个数;
父亲;
左右儿子编号;
节点权值;
权值出现次数;
子树大小。
三.Splay 的操作#
-
1. pushup#
在改变节点位置后,将节点 的子树大小 值更新:
void pushup (int u) { siz[u] = siz[ch[u][0]] + siz[ch[u][1]] + cnt[u]; } -
2. get#
判断节点 是父亲节点的左儿子还是右儿子:
bool get (int u) {return u == ch[u][1];} -
3. clear#
销毁节点 :
void clear (int u) { ch[u][0] = ch[u][1] = fa[u] = val[u] = siz[u] = cnt[u] = 0; } -
4. rotate#
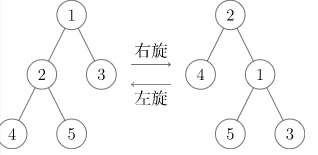
将节点 左旋转或者右旋转向上一层,这是为了保证 的平衡。
可以看做左旋为顺时针方向,右旋为逆时针方向。旋转需要保证以下三条要求:
- 整棵 的中序遍历不变(需要满足二叉查找树的性质)
- 受影响的节点维护的信息依然正确有效
- 必须指向旋转后的根节点
分析一下旋转操作:
首先设需要旋转的节点为 ,其父亲节点为 ,以右旋为例:- 将 的左儿子指向 的右儿子,且 的右儿子的父亲指向 :
ch[y][0] = ch[x][1]; fa[ch[x][1]] = y; - 将 的右儿子指向 ,且 的父亲指向 ;
ch[x][1] = y; fa[y] = x; - 如果原来的 有父亲 ,那么把 的某个儿子,也就是原来 所在的儿子位置 指向 ,且 的父亲指向 。
fa[x] = z; if (z) ch[z][y == ch[z][1]] = x;
综合起来的代码如下:
void rotate (int x) { int y = fa[x], z = fa[y], chk = get (x); ch[y][chk] = ch[x][chk ^ 1]; if (ch[x][chk ^ 1]) { fa[ch[x][chk ^ 1]] = y; } ch[x][chk ^ 1] = y; fa[y] = x; fa[x] = z; if (z) { ch[z][y == ch[z][1]] = x; } pushup (y); pushup (x); }由于左旋和右旋是两种相反的操作,所以我们可以融合到一个函数中,也就出现了 的操作。
-
5. splay#
操作规定:每次访问一个点都要将其旋转至根节点。
也就是说 操作就是将一个点旋转到根节点上。
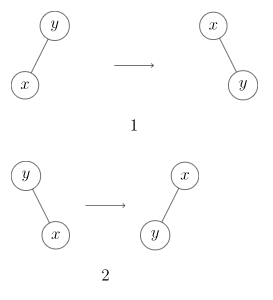
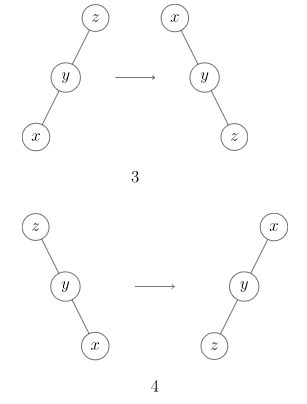
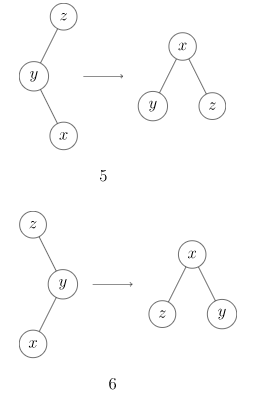
接下来对于 的 种情况进行讨论:经过这 种情况模拟我们得知:
当 的父亲的父亲存在时:
- 和 的父亲和 的父亲的父亲三个点在同一直线上时,旋转 的父亲;
- 否则旋转 点。
代码如下:
void splay (int x, int aim) {//将 x 旋转到 aim 的儿子处 for (int f = fa[x]; f = fa[x], f != aim; rotate (x)) {//不断旋转 if (fa[f] != aim) { rotate (get (x) == get (f) ? f : x); } } if (!aim) { root = x;//修改根节点 } } -
6. insert#
设插入的值为 ,分三种情况:
- 如果树为空,则直接插入根并退出。
- 如果当前节点的权值等于 ,则增加当前节点的大小,并更新节点与父亲的信息,将当前节点进行 操作。
- 否则按二叉查找树的性质向下寻找,找到空节点插入,再进行 操作。
void insert (int k) { if (!root) {//树为空 val[++ tot] = k; cnt[tot] ++; root = tot; pushup (root); //新建节点 return ; } int now = root, f = 0; while (1) { if (val[now] == k) {//找到权值相同的节点 cnt[now] ++;//增加大小 pushup (now); pushup (f); splay (now, 0);//旋转到根 break; } f = now;//向下搜索 now = ch[now][val[now] < k]; //当前点权值小于k,则在右儿子处 //当前点权值大于k,则在左儿子处 if (!now) {//找到空节点 val[++ tot] = k; cnt[tot] ++; fa[tot] = f; ch[f][val[f] < k] = tot;//父亲节点的子节点更新 pushup (tot); pushup (f); splay (tot, 0);//旋转到根 //新建节点 break; } } } -
7. get_rank#
查询 值的排名。
根据二叉查找树的定义和性质,可以按照以下步骤查询 的排名。- 如果 比当前点的权值小,向它的左子树搜索。
- 如果 比当前点的权值大,将答案加上左子树的大小和当前节点的大小,然后向右子树搜索。
- 如果 与当前点的权值相同,返回当前的答案 。
代码如下:
int get_rank (int k) { int res = 0, now = root; while (1) { if (k < val[now]) { now = ch[now][0];//向左子树搜索 } else { res += siz[ch[now][0]];//增加排名 if (k == val[now]) { splay (now, 0);//不要忘记这一步 return res + 1; } res += cnt[now];//增加排名 now = ch[now][1];//向右子树搜索 } } } -
8. get_kth#
查询排名为 的权值。
分以下两种情况:- 如果左子树非空,且剩余排名 不大于左子树的大小 ,向左子树搜索。
- 否则将 减去左子树和根的大小。如果此时 的值小于等于 ,那么返回根节点的值。否则继续向右子树搜索。
代码如下:
int get_kth (int k) { int now = root; while (1) { if (ch[now][0] && k <= siz[ch[now][0]]) { now = ch[now][0];//向左子树搜索 } else { k -= cnt[now];//减去当前节点大小 k -= siz[ch[now][0]];//减去左子树大小 if (k <= 0) { splay (now, 0);//不要忘记了! return val[now]; } now = ch[now][1];//向右子树搜索 } } } -
9. get_pre#
查询点 的前驱,即最大的小于 的数。
那么可以将 插入 (此时 在根节点),前驱也就是 的左子树中最右的节点,最后将 删除即可。
代码如下:int get_pre () { int now = ch[root][0]; if (!now) { return now; } while (ch[now][1]) { now = ch[now][1];//在左子树中寻找最右的节点。 } splay (now, 0);//不要忘记! return now; } -
10. get_suf#
查询点 的后继,也就是最小的大于 的数。
查询方法与前驱相似,查找 的右子树中最左的节点。
代码如下:int get_suf () { int now = ch[root][1]; if (!now) { return now; } while (ch[now][0]) { now = ch[now][0]; } splay (now, 0); return now; } -
11. merge#
合并两棵 。设两棵树的根节点分别为 和 ,那要求 中的最大值小于 中的最小值。合并操作如下:
- 如果 和 中有一棵空树或都是空树,那么返回非空树或空树。
- 否则将 中的最大值 到根节点,将它的右子树设置为 并更新节点的信息,然后返回这个节点。
-
12. delete#
删除点 。
首先将 旋转到 的位置上:
- 如果 ,那么将 后退出即可;
- 否则合并它的两棵子树即可。
代码如下:
void del (int k) { get_rank (k);//将k旋转到根 if (cnt[root] > 1) { cnt[root] --;//直接减 pushup (root); return ; } if (!ch[root][0] && !ch[root][1]) { clear (root);//没有儿子,直接销毁 root = 0; return ; } if (!ch[root][0]) {//只有右子树 int now = root; root = ch[root][1]; fa[root] = 0; clear (now); return ; } if (!ch[root][1]) {//只有左子树 int now = root; root = ch[root][0]; fa[root] = 0; clear (now); return ; } int now = root, x = get_pre (); fa[ch[now][1]] = x; //根变为原来的根的前驱, //那么原来的右儿子的父亲就变为原来的根的前驱 ch[x][1] = ch[now][1];//前驱的右儿子变为原来根的右儿子 clear (now);//销毁原来的根 pushup (root); }
四.例题讲解#
P3369 【模板】普通平衡树#
模板题。将上文讲到的操作融合即可。
代码如下:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 7;
int rt[N], tot = 0, fa[N], ch[N][2], val[N], cnt[N], siz[N], root;
struct Splay {
inline void pushup (int u) {
siz[u] = siz[ch[u][0]] + siz[ch[u][1]] + cnt[u];
}
inline bool get (int u) {
return u == ch[fa[u]][1];
}
inline void clear (int u) {
ch[u][0] = ch[u][1] = fa[u] = val[u] = siz[u] = cnt[u] = 0;
}
inline void rotate (int x) {
int y = fa[x], z = fa[y], chk = get (x);
ch[y][chk] = ch[x][chk ^ 1];
if (ch[x][chk ^ 1]) {
fa[ch[x][chk ^ 1]] = y;
}
ch[x][chk ^ 1] = y;
fa[y] = x;
fa[x] = z;
if (z) {
ch[z][y == ch[z][1]] = x;
}
pushup (y);
pushup (x);
}
inline void splay (int x, int aim = 0) {
for (int f = fa[x]; f = fa[x], f != aim; rotate (x)) {
if (fa[f] != aim) {
rotate (get (x) == get (f) ? f : x);
}
}
if (!aim) {
root = x;
}
}
inline void insert (int k) {
if (!root) {
val[++ tot] = k;
cnt[tot] ++;
root = tot;
pushup (root);
return ;
}
int now = root, f = 0;
while (1) {
if (val[now] == k) {
cnt[now] ++;
pushup (now);
pushup (f);
splay (now, 0);
break;
}
f = now;
now = ch[now][val[now] < k];
if (!now) {
val[++ tot] = k;
cnt[tot] ++;
fa[tot] = f;
ch[f][val[f] < k] = tot;
pushup (tot);
pushup (f);
splay (tot, 0);
break;
}
}
}
int get_rank (int k) {
int res = 0, now = root;
while (1) {
if (k < val[now]) {
now = ch[now][0];
}
else {
res += siz[ch[now][0]];
if (k == val[now]) {
splay (now, 0);
return res + 1;
}
res += cnt[now];
now = ch[now][1];
}
}
}
int get_kth (int k) {
int now = root;
while (1) {
if (ch[now][0] && k <= siz[ch[now][0]]) {
now = ch[now][0];
}
else {
k -= cnt[now];
k -= siz[ch[now][0]];
if (k <= 0) {
splay (now, 0);
return val[now];
}
now = ch[now][1];
}
}
}
int get_pre () {
int now = ch[root][0];
if (!now) {
return now;
}
while (ch[now][1]) {
now = ch[now][1];
}
splay (now, 0);
return now;
}
int get_suf () {
int now = ch[root][1];
if (!now) {
return now;
}
while (ch[now][0]) {
now = ch[now][0];
}
splay (now, 0);
return now;
}
void del (int k) {
get_rank (k);
if (cnt[root] > 1) {
cnt[root] --;
pushup (root);
return ;
}
if (!ch[root][0] && !ch[root][1]) {
clear (root);
root = 0;
return ;
}
if (!ch[root][0]) {
int now = root;
root = ch[root][1];
fa[root] = 0;
clear (now);
return ;
}
if (!ch[root][1]) {
int now = root;
root = ch[root][0];
fa[root] = 0;
clear (now);
return ;
}
int now = root, x = get_pre ();
fa[ch[now][1]] = x;
ch[x][1] = ch[now][1];
clear (now);
pushup (root);
}
}tree;
int n, op, x;
int main () {
scanf ("%d", &n);
for (int i = 1; i <= n; i ++) {
scanf ("%d%d", &op, &x);
if (op == 1) {
tree.insert (x);
}
if (op == 2) {
tree.del (x);
}
if (op == 3) {
printf ("%d\n", tree.get_rank (x));
}
if (op == 4) {
printf ("%d\n", tree.get_kth (x));
}
if (op == 5) {
tree.insert (x);
printf ("%d\n", val[tree.get_pre ()]);
tree.del (x);
}
if (op == 6) {
tree.insert (x);
printf ("%d\n", val[tree.get_suf ()]);
tree.del (x);
}
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App
· 张高兴的大模型开发实战:(一)使用 Selenium 进行网页爬虫