「学习笔记」单调栈

一.单调栈的概念#

单调栈就是满足单调性的栈结构。与单调队列相比，它仅在一端进出。

二.单调栈的操作#

如图所示，栈中从顶到底的元素依次为 ${0,3,5,7}$。

插入元素 $4$ 时，为了保证单调性，需要依次弹出元素 $0,3$，操作后栈变为 $4,5,7$。

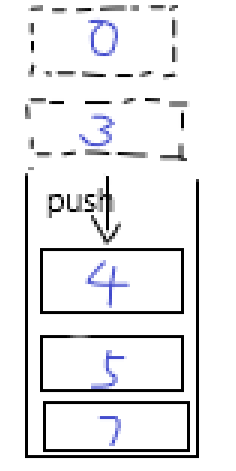
用代码表示如下：

Copy
int x;
stack<int> st;
while (!st.empty() && st.top () <= x) {
	st.pop ();
}
st.push (x);

三.例题讲解#

P5788 【模板】单调栈#

单调栈模板。

题意就是向后找，求第一个大于这个数的下标。

我们可以倒序处理，用单调栈维护即可。

核心代码如下：

Copy
for (int i = n; i >= 1; i --) {
	while (!st.empty() && a[st.top()] <= a[i]) {
		st.pop();//弹出栈中小于该数的数字。
	}
	if (st.empty()) {
		f[i] = 0;
	}
	else {
		f[i] = st.top();
	}
	st.push (i);//单调栈中存储编号。
}

P2866 [USACO06NOV]Bad Hair Day S#

非常板子的一道题了。

维护一个单调序列，对于当前的牛，弹出栈中身高小于它的牛，栈的大小就是这头牛的贡献。

核心代码如下：

Copy
for (int i = 1, x; i <= n; i ++) {
	cin >> x;
	while (!st.empty () && st.top () <= x) {
		st.pop ();//弹出栈中比它小的元素。
	}
	ans += st.size ();
	st.push (x);
}

P6510 奶牛排队#

题意：求一个区间，使得左端点最小，右端点最大，且区间内不存在与两端点相同的元素，求这个区间的最大长度。

设左端点为 $L$，右端点为 $R$。

因为 $L$ 是区间内最小的，所以 $[L,R]$ 中的元素都 $>L$，所以只要 $L$ 右侧第一个 $\le L$ 的奶牛位于 $R$ 的右侧，则 $L$ 合法。

因为 $R$ 是区间内最大的，所以 $[L,R]$ 中的元素都 $<R$，所以只要 $R$ 左侧第一个 $\ge L$ 的奶牛位于 $L$ 的左侧，则 $R$ 合法。

那么我们可以用单调栈维护当前左侧第一个 $\ge$ 和右侧第一个 $\le$。然后枚举右端点，更新答案即可。

寻找左侧第一个 $\ge$：

Copy
for (int i = 1; i <= n; i ++) {
	while (!s.empty () && s.top ().h < h[i]) {
		s.pop ();//弹出小于当前元素的。
	}
	if (!s.empty ()) {
		l[i] = s.top ().num;
	}
	else {
		l[i] = 0;
	}
	Node tmp;
	tmp.h = h[i];
	tmp.num = i;
	s.push (tmp);
}

寻找右侧第一个 $\le$：

Copy
for (int i = n; i >= 1; i --) {
	while (!s.empty () && s.top ().h > h[i]) {
		s.pop ();//弹出大于当前元素的。
	}
	if (!s.empty ()) {
		r[i] = s.top ().num;
	}
	else {
		r[i] = n + 1;
	}
	Node tmp;
	tmp.h = h[i];
	tmp.num = i;
	s.push (tmp);
}

P1901 发射站#

还是板子题。

对于当前元素，对于所有比它小的元素，我们全部弹出。

因为被弹出的元素是单调递增且小于当前元素的，那么当前元素可以接收到弹出元素的能量。

单调栈维护一个单调递减的序列即可。

核心代码如下：

Copy
for (int i = 1; i <= n; i ++) {
	while (!st.empty () && h[st.top ()] < h[i]) {
		ans[i] += v[st.top ()];//比当前元素小的都弹出栈，并累加答案。
		st.pop ();
	}
	if (!st.empty ()) {
		ans[st.top ()] += v[i];
	}
	st.push (i);
}