「学习笔记」网络流
一.网络流的一些概念
网络流:一种类比水流的解决问题的方法。
网络:相当于有源点和汇点的有向图。
弧:可以理解为有向边。
源点:可以理解为起点,有无限的水。
汇点:可以理解为终点。
弧的残留容量:也就是这条弧的容量减去流量。
残量网络:指每条弧都有残留容量的网络。
增广路:一条在残留网络中的路径,且路径上的每条边的残留容量都是正数。
二.最大流
P3376 【模板】网络最大流
最大流也就是源点能接收的流量最大值。
这里有一个很重要的定理:
增广路定理:流量网络达到最大值时当且仅当残量网络中没有增广路。
增广路方法:称为 \(FF\) 算法,不断在残留网络中找源点到汇点的增广路,根据木桶定律从源点发送流量(也就是发送流量为增广路中最小的弧的残留容量),并且修改弧的残留容量,直到残留网络上没有增广路。
寻找增广路的代码如下:
inline bool bfs () {
//dis数组是能流的最大值。
//s是起点,t是终点。
queue<int> q;
memset (vis, false, sizeof (vis));
q.push (s);
dis[s] = inf;//起点的容量为inf。
vis[s] = true;
while (!q.empty()) {
int u = q.front ();
q.pop ();
for (int i = head[u]; i; i = e[i].nxt) {
if (e[i].w == 0) {//不考虑残留容量为0的边。
continue;
}
int v = e[i].to;
if (vis[v] == true) {
continue;
}
dis[v] = min (dis[u], e[i].w);//根据木桶定律可流流量取min值。
pre[v] = i;//记录前驱。
q.push (v);
vis[v] = true;
if (v == t) {
return true;//到了汇点就找到了增广路。
}
}
}
return false;
}
然后我们就要用\(EK\)算法了。
\(EK\)算法的核心就在于不断用\(BFS\)寻找增广路并不断更新最大流量值,直到网络上不存在增广路为止。
实现过程分为两个函数:
\(1.\) 寻找增广路。\(2.\) 更新增广路上的残留容量。
第一个函数上文讲过了,接下来介绍第二个函数。
我们要算出每条增广路上残留容量的最小值 \(dis\),然后最大流就可以增加 \(dis\),增广路上的每条正向边都减去 \(dis\),反向边都加上 \(dis\)。
为什么要建反向边呢?这是 \(EK\) 算法中的重点!
因为一条边有可能被多条增广路所包含!
但有可能我们第一次选择的增广路并不是最优选择,而构建反向边就相当于给了一个反悔的操作。
在第二次经过这条边的时候,我们就可以通过反向边来将这条边恢复。
相当于我们加上反向边跑 \(EK\) 算法,就能保证得到的是最优答案。
建立反向边能让被多条增广路包含的边的流量最大化,也就达到了汇点流量最大化。
通俗点说,让这条被多条增广路包含的边被“榨干”,而通过遍历反向边就可以达到这个效果。
下面给出图来讲解过程:
黑边是正向边,红边是反向边,蓝字是正向边权,红字是反向边权,ans是最大流。
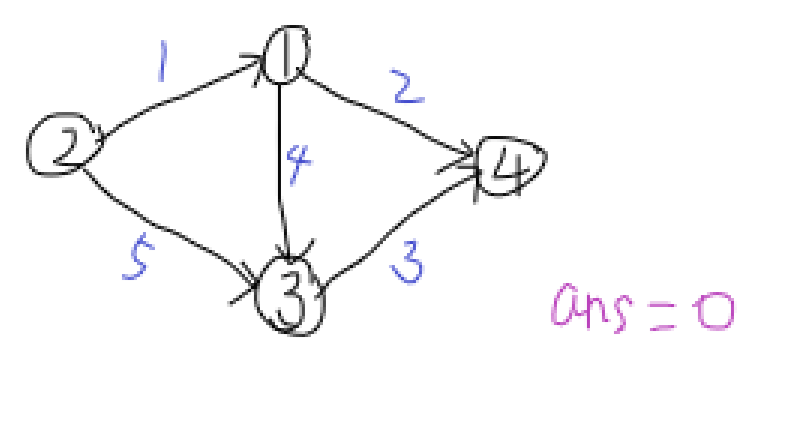
这是原图。
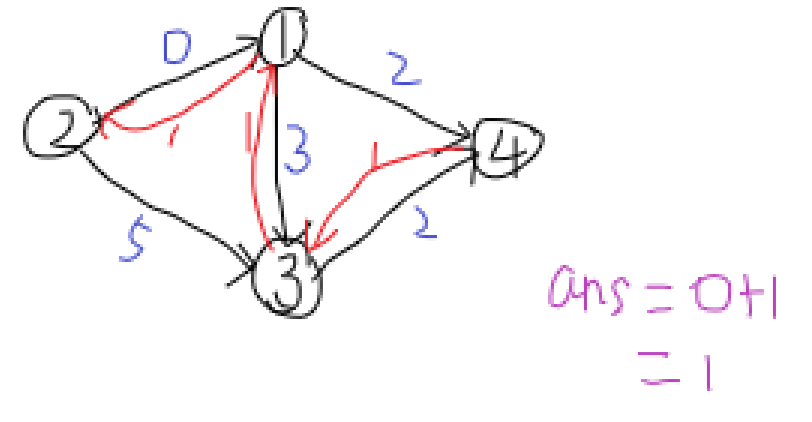
找到增广路 \(2\to1\to3\to4\),流量为 \(1\)。
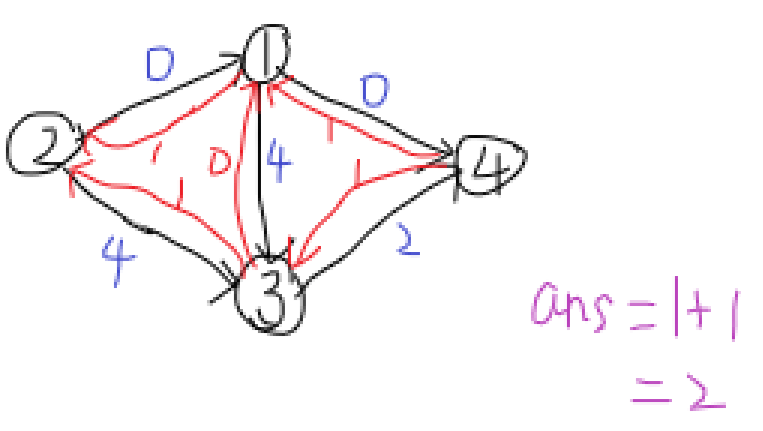
找到增广路 \(2\to3\to1\to4\),其中边 \(3\to1\) 走反向边,流量为 \(1\)。
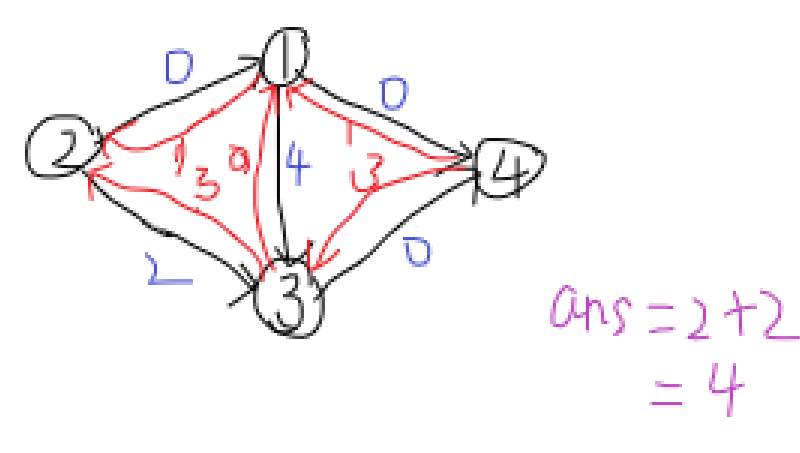
找到增广路 \(2\to3\to4\),流量为 \(2\)。
然后残量网络中没有增广路了,最终最大流为 \(4\)。
代码如下:
inline void EK () {
int ed = t;//t是汇点。
//dis[t] 是流向汇点的流量。
while (ed != s) {
int v = pre[ed];
e[v].w -= dis[t];//正向边减去流量。
e[v ^ 1].w += dis[t];//反向边加上流量。
ed = e[v ^ 1].to;//沿着增广路更新。
}
ans += dis[t];//最大流加上汇点的流量。
}
Tip:关于存储反向边,我们在邻接表中成对存储,也就是 \(1,2\) 一对, \(1,2\) 一对。因为这样我们就可以在修改边权时将正向边 \(xor1\) 得到反向边。
注意,在最初建边时要将正向边的起始编号设为 \(1\) 而不是 \(0\)。
这样正向边编号就是奇数, \(xor1\) 后就能 \(+1\) 从而得到反向边。
时间复杂度:
每条边最多被增广 \(\frac{n}{2} - 1\) 次,共有 \(m\) 条边,那总增广次数就是 \(nm\)。
一次 \(bfs\) 找增广路的最多要遍历 \(m\) 条边,那么总复杂度就是 \(O(nm^2)\)。
P2740 [USACO4.2]草地排水Drainage Ditches
这道题就是求最大流, \(EK\) 算法套上去就可以了。
三.最小费用最大流
P3381 【模板】最小费用最大流
这道题在最大流的前提下增加了最小费用的条件。
我们知道,流向汇点的最大流是唯一的,但是流的方法是不唯一的。
而我们原先的 \(bfs\) 不能完成是因为只选增广路而没有考虑最小花费。
那我们可以将 \(bfs\) 改造成最短路径算法,相当于在残量网络中的最短路径上跑最大流算法。
这样就能完美解决这个问题。
但由于有可能有负权,那我们就只能用 \(SPFA\) 算法了。
inline bool bfs () {
queue<int> q;
q.push (s);
memset (dis, inf, sizeof (dis));//dis为价格。
memset (vis, false, sizeof (vis));
vis[s] = true;//vis是是否在队列中。
flow[s] = inf;//起点的流量为 inf。
dis[s] = 0;//SPFA 算法中,起点的dis值为0。
while (!q.empty ()) {
int u = q.front ();
q.pop ();
vis[u] = false;
for (int i = head[u]; i; i = e[i].nxt) {
if (e[i].flow == 0) continue;//不走流量为0的边。
int v = e[i].to;
if (dis[v] > dis[u] + e[i].dis) {//最短路径
dis[v] = dis[u] + e[i].dis;
pre[v] = i;//记录前驱。
flow[v] = min (flow[u], e[i].flow);//路上最小容量。
if (vis[v] == false)
q.push (v),vis[v] = true;
}
}
}
if (dis[t] == inf)
return false;//不能到达汇点就是没有增广路。
return true;
}
int maxflow = 0, mincost = 0;
inline void MCMF () {
while (bfs () == true) {//不断找增广路。
int x = t;
while (x != s) {
int v = pre[x];
e[v].flow -= flow[t];
e[v ^ 1].flow += flow[t];
x = e[v ^ 1].to;
}
maxflow += flow[t];
mincost += dis[t] * flow[t];//花费是数量乘以单价。
}
}
时间复杂度与求最大流一样,为 \(O(nm^2)\)。
这个时候就有人问了, \(SPFA\) 不是死了吗?
由于有负边权我们不得不用 \(SPFA\)。
但是但是但是!
我们只要让负边权全变为正边权就可以了。
我的「学习笔记」Johnson 全源最短路 中有提到这个技巧,大家可以去学习。
这里是可以保证没有负环的,所以不需要用 \(SPFA\) 判断负环。
四.Dinic算法
我们发现在 \(EK\) 算法中效率较低的原因在于每一次 \(bfs\) 只能找到一条增广路。
那我们就采用一次 \(bfs\) 分层,然后用 \(dfs\) 多路增广找到最短的增广路,这样效率就飞速提升了。
算法分为两步:
\(1.\) 采用 \(bfs\) 将图分层,按照经过的边数把图分层,每次考虑点 \(u\) 时都只考虑下一层的点 \(v\),这样就能保证不混乱。
\(2.\) 采用 \(dfs\) 多路增广,当点 \(u\) 到达下一层的点 \(v\) 时,点 \(v\) 直接尝试到达汇点,然后到达汇点后就可以在增广路上找到增广的量。如果 \(u\) 的残留容量仍然大于 \(0\),那么就继续到点 \(u\) 下一层的别的点继续找增广路。
这个方法也是搭建在 \(EK\) 算法的基础上的,正确性可以保证。因为只要图中还有增广路,我们 \(bfs\) 分层后的多路增广也能找到增广路。
最后当没有增广路,停止循环。
代码如下:
inline int bfs () {
queue<int> q;
memset (dep, 0, sizeof (dep));//初始化。
q.push (s);
dep[s] = 1;//起点为第一层。
while (!q.empty ()) {
int u = q.front ();
q.pop ();
for (int i = head[u]; i; i = e[i].nxt) {
if (e[i].w == 0) {//不走流量为0的边。
continue;
}
int v = e[i].to;
if (dep[v] == 0) {
dep[v] = dep[u] + 1;//设置dep。
q.push (v);
}
}
}
return dep[t] != 0;
//如果不为0就代表到达了汇点,也就是有增广路。
}
ll dfs (int u, ll in) {//u表示当前点,in表示流到当前点的流量。
if (u == t) {
return in;//到达汇点时,流到当前点的流量就是增广路的流量。
}
ll out = 0;
for (int i = head[u]; i && in; i = e[i].nxt) {//要保证流量为正数!!!
if (e[i].w == 0) {//不走流量为0的边。
continue;
}
int v = e[i].to;
if (dep[v] == dep[u] + 1) {//只走下一层的点。
ll temp = min (e[i].w, in);//这条路径的流量
ll now = dfs (v, temp);//从点u到汇点的增广路的流量。
e[i].w -= now;//正向边减。
e[i ^ 1].w += now;//反向边加。
in -= now;//流过来的总量减。
out += now;//能流出的总量加。
}
}
if (out == 0)
dep[u] = 0;//不能流出就标记。
return out;
}
在累计答案的时候,我们不断分层找增广路,多路增广时要将初始流量设为 \(inf\),因为能流的量是无穷大的。
五.当前弧优化
当前弧优化也就是去除颓余的操作。
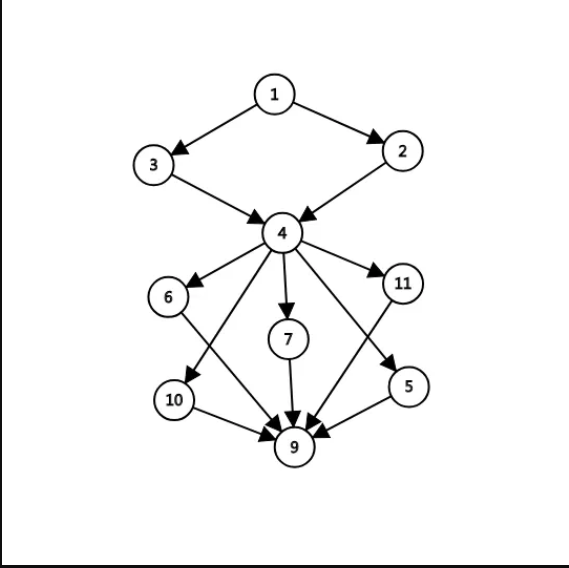
如图所示,当我们找到增广路 \(1\to3\to4\to7\to9\) 后,很多条路径都没有可以被增广的可能性了。
那我们就设置一个一个 \(cur\) 数组,表示上一次该点遍历到的边,也就是当前弧。
\(cur\) 数组也就相当于建边时的 \(head\) 数组,多路增广时我们从 \(cur_{当前点}\) 开始遍历就可以了。
初始化时将 \(cur_x=head_x\)。
唯一改变的代码如下:
for (int i = cur[u]; i && in; i = e[i].nxt) {//从当前弧开始。
cur[u] = i;//记录当前弧。
if (e[i].w == 0)
continue;
int v = e[i].to;
if (dep[v] == dep[u] + 1) {
ll now = dfs (v, min (e[i].w, in));
e[i].w -= now;
e[i ^ 1].w += now;
in -= now;
out += now;
}
//除前两行之外没有改动。
}
在稠密图中当前弧优化的优化效果巨大!
六.参考资料
https://www.luogu.com.cn/blog/yxz874544095/solution-p3376
https://www.luogu.com.cn/blog/cicos/Dinic
https://www.cnblogs.com/Xing-Ling/p/11487554.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号