「学习笔记」线段树
零.前言
由于作者仍然不断地学习关于线段树的知识,所以该学习笔记的内容将不断填充。
这里给出一份洛谷题单供大家参考,为该学习笔记的例题。
欢迎点赞关注收藏。
一.概念
线段树是一种二叉搜索树,每个节点最多有两颗子树,通常称为左、右子树。
这个数据结构将一个区间分成若干个区间,每一个节点存储一个区间 \([L,R]\) 的信息,叶子结点的 \(L\) 等于 \(R\)。
也就是说,我们将 \([1,n]\) 平均分为两个区间,然后一直执行这个操作,分到无法再分为止。
线段树的思想和分治很像:将大区间的信息分为若干个小区间的信息进行操作。
二.建树
首先我们要有一个结构体封装节点信息:
struct SegMentTree {
int l;//区间左端点。
int r;//区间右端点。
int sum;//区间和。
int siz;//区间长度。
//Do other things.
}S[N];
我们有一个数组 \([1,2,3,4,5]\),线段树的搭建如下。
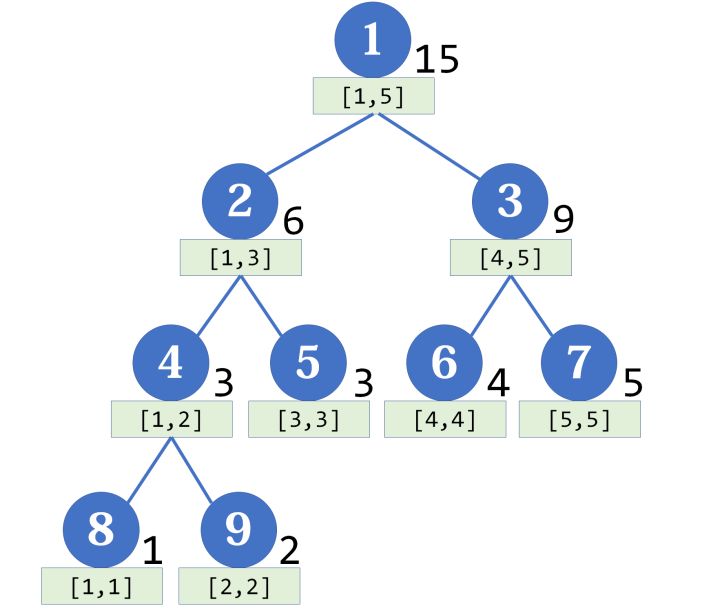
可以发现,对于一个节点 \(u\),它的左子节点和右子节点的编号分别为 \(2u\) 和 \(2u+1\),这样我们就能从根节点一直递归下去建树。
显然,节点 \(u\) 的区间和为它的左子节点和右子节点的区间和之和。
这样,就可以写出建树代码了:
#define ls (x) (x * 2)//左子节点。
#define rs (x) (x * 2 + 1)//右子节点。
void build (int nd, int l, int r) {
s[nd].l = l, s[nd].r = r, s[nd].siz = r - l + 1;
//记录信息。
if (l == r) {
s[nd].sum = a[l];//a数组为最初给定的数列。
return ;
}
int mid = l + r >> 1;
build (ls(nd), l, mid);
build (rs(nd), mid + 1, r);
//递归左子树和右子树。
s[nd].sum = s[ls(nd)].sum + s[rs(nd)].sum;
//合并信息。
}
三.区间查询
其实单点查询没什么必要学,区间查询可以实现单点查询。
那么这里就只讲解区间查询。
对于一个区间 \([L,R]\),我们要查询它的区间之和。
同样需要递归记录和。
考虑一个节点 \(u\), 设它的左端点为 \(u_l\),右端点为 \(u_l\),询问区间为 \([L,R]\)。
如果 \(L\le u_l\) 并且 \(R \ge u_r\),那么直接返回当前节点的区间和即可。
也就是说当当前节点是询问范围的子集时,就直接返回当前节点的区间和。
如果不满足上述条件,那么就需要递归两个子树,通过合并两个区间的信息获得该区间的答案。
这样很容易得出代码了:
ll query (int nd, int l, int r) {
if (l <= s[nd].l && r >= s[nd].r) {
return s[nd].sum;
//当前节点是询问范围的子集时,就直接返回当前节点的区间和。
}
int mid = s[nd].l + s[nd].r >> 1;
ll res = 0;
if (l <= mid) {
res += query (ls(nd), l, r);
//左子树与询问区间有交集,那么递归左子树。
}
if (r > mid) {
res += query (rs(nd), l, r);
//右子树与询问区间有交集,那么递归右子树。
}
return res;
}
当然,如果需要单点查询节点 \(u\),那么直接将询问区间左右端点都设为 \(u\) 即可。
四.区间加法
给定一个区间 \([l,r]\),要求给每个区间中的数增加 \(k\)。
这时候暴力的想法冒出来了。但是暴力遍历区间进行操作的话,时间难以承受。
这里给一个小故事来启发大家的思路:
同学 \(u\) 很喜欢借别人的钱,但是他觉得每借 \(1\) 次就还别人 \(1\) 次钱实在是太麻烦了!于是,他想到了一个好方法。
一天,他对最经常借他钱的同学 \(v\) 说:"前几天我一共借了你 \(76\) 元,今天我再借你 \(15\) 元。但是我先不还给你,等到你需要用钱的时候我再还给你。"
小 \(v\) 说:"这样是挺好,能减少你的还钱的操作,方便。但是你和我如果都不记得你借了我多少钱怎么办呢?"
小 \(u\) 说:"你放心,我拿一个小本本记着的,你需要钱的时候我就会还给你滴!"
于是,小 \(u\) 和小 \(v\) 一言为定,双方都达成了自己的愿望。
看到这里,大家应该都有想法了。
对于一个节点,我们需要一个变量记录改变的数量,通常我们称为懒惰标记。
如果当前节点的懒惰标记为 \(0\),也就是说无需下传标记了。
对于下传懒惰标记,我们可以单独写一个函数:
inline void pushdown (int nd) {
s[ls(nd)].add += s[nd].add;
s[rs(nd)].add += s[nd].add;
//记录懒惰标记
s[ls(nd)].sum += (s[ls(nd)].siz * s[nd].add);
s[rs(nd)].sum += (s[rs(nd)].siz * s[nd].add);
//左右子树的每个数都需要加上父节点的懒惰标记,那么区间和只需要乘上区间长度即可。
s[nd].add = 0;//下传过了就无需下传啦!
}
对于区间修改,按照上文区间查询一样的思路,对于三种情况进行分类讨论:
void Add (int nd, int l, int r, int k) {
//k为增加的数字,l和r是询问区间。
if (l <= s[nd].l && r >= s[nd].r) {
//当前区间是询问区间的子集时。
s[nd].sum += s[nd].siz * k;
s[nd].add += k;
return ;
}
if (s[nd].add) {
pushdown (nd);
}
int mid = s[nd].l + s[nd].r >> 1;
if (l <= mid) {
Add (ls(nd), l, r, k);
//递归修改左子树。
}
if (r > mid) {
Add (rs(nd), l, r, k);
//递归修改右子树。
}
s[nd].sum = s[ls(nd)].sum + s[rs(nd)].sum;
//合并左右区间。
}
当然,在有区间修改的时候,区间查询时,也是需要下传懒惰标记的。
五.基础运用
P3372 【模板】线段树 1
单点修改,区间查询。
P2357 守墓人
单点修改,区间查询。
P2068 统计和
区间修改,区间查询。
P2846 [USACO08NOV]Light Switching G
区间异或,区间查询。下传懒惰标记和修改的时候稍微改改即可。
P3870 [TJOI2009]开关
同上题。
SP7259 LITE - Light Switching
同上题。
P5057 [CQOI2006]简单题
同上题。
五倍经验!
因为之前写的代码太丑就不放了qwq。
六.区间乘法
上文我们提到过,对于区间加法时,我们创造出一个懒惰标记记录。
同样,对于区间乘法,我们也需要一个懒惰标记进行标记。
我们知道,乘法和加法的优先级不同,也就是说,我们不能将乘法和加法的信息混在一起,所以需要两个标记进行处理。
思想透彻了,其实代码实现也很简单。
下传标记如下:
inline void pushdown (int nd) {
s[ls(nd)].mul = s[nd].mul * s[ls(nd)].mul;
s[rs(nd)].mul = s[nd].mul * s[rs(nd)].mul;
//维护乘法懒惰标记。
s[ls(nd)].add = s[nd].mul * s[ls(nd)].add + s[nd].add;
s[rs(nd)].add = s[nd].mul * s[rs(nd)].add + s[nd].add;
//需要乘上乘法懒惰标记。
s[ls(nd)].sum = s[ls(nd)].siz * s[nd].add + s[nd].mul * s[ls(nd)].sum;
s[rs(nd)].sum = s[rs(nd)].siz * s[nd].add + s[nd].mul * s[rs(nd)].sum;
s[nd].add = 0;
s[nd].mul = 1;
}
对于区间乘法,我们的操作像区间加法一样,递归左右子树进行修改。
代码如下:
void Mul (int nd, int l, int r, int k) {
if (l <= s[nd].l && r >= s[nd].r) {
s[nd].mul *= k;
s[nd].add *= k;
s[nd].sum *= k;
//处理叶子节点信息。
return ;
}
pushdown (nd);
//下传标记。
int mid = s[nd].l + s[nd].r >> 1;
if (l <= mid) {
Mul (ls(nd), l, r, k);
}
if (r > mid) {
Mul (rs(nd), l, r, k);
}
//递归左右子树。
pushup (nd);
//合并区间信息。
}
七.区间最值
其实思想都是一样的,和查询一样,分三种情况进行处理,递归左右子树。
查询区间最小值如下:
int Query_Min (int nd, int l, int r) {
if (l <= s[nd].l && r >= s[nd].r) {
return s[nd].mn;
//直接返回。
}
int mid = s[nd].l + s[nd].r >>1, ans = inf;
if (l <= mid) {
ans = min (ans, Query_Min (ls(nd), l, r));
//左子树找最小值。
}
if (r > mid) {
ans = min (ans, Query_Min (rs(nd), l, r));
//右子树找最小值。
}
return ans;
}
查询最大值将符号换一下即可。
八.基础运用
P3373 【模板】线段树 2
区间加法,乘法,询问。
P5097 [USACO04OPEN]Cave Cows 2
区间查询最小值,懒惰标记都不需要。
P2880 [USACO07JAN]Balanced Lineup G
求极差,区间查询最大值以及最小值即可。
区间查询最小值。
区间查询最小值。
九.区间开方
SP2713 GSS4 - Can you answer these queries IV
区间开方的模板题。
首先我们发现一个性质:\(10^{18}\) 经过 \(6\) 次开方(向下取整)后就变成了 \(1\)。
也就是说,对于任意一个区间,最多只可能被开方(向下取整)\(6\) 次。因为 \(1\) 继续开方(向下取整)后一直都是 \(1\)。
于是,我们只需要记录每个区间的最大值,当该区间最大值为 \(1\) 时,就可以退出,否则直接使用 \(sqrt\) 函数暴力修改即可。
void Sqrt (int nd, int l, int r, int tl, int tr) {
if (maxx[nd] <= 1) {
return ;
}
if (l == r) {
s[nd] = sqrt (s[nd]);
maxx[nd] = s[nd];
//暴力修改。
return ;
}
int mid = l + r >> 1;
if (tl <= mid) {
Sqrt (ls(nd), l, mid, tl, tr);
}
if (tr > mid) {
Sqrt (rs(nd), mid + 1, r, tl, tr);
}
pushup (nd);
}
十.区间取模
给出一个很显然的结论:
我们可以参考区间开方的思想,也就是说,一个区间最多被取模 \(\log x\) 次。
所以,只需要记录当前区间的最大值,如果最大值小于 \(p\) 就可以直接退出。
否则暴力取模。
void Mod (int nd, int l, int r, int tl, int tr, int p) {
if (mx[nd] < p) {
return ;
}
if (l == r) {
sum[nd] %= p;
mx[nd] %= p;
return ;
}
int mid = l + r >> 1;
if (tl <= mid) {
Mod (ls(nd), l, mid, tl, tr, p);
}
if (tr > mid) {
Mod (rs(nd), mid + 1, r, tl, tr, p);
}
pushup (nd);
}

