「学习笔记」Johnson 全源最短路
一.问题引入
给定一个包含 \(n\) 个结点和 \(m\) 条带权边的有向图,求所有点对间的最短路径长度。
在解决最短路问题时,负边权的情况是经常遇到的。
而这道题目要求求全源最短路径,我们会想到三个做法:
\(1.\) Spfa单源最短路径算法,时间复杂度为 \(O(nm)\)。求全源最短路径,枚举起点时间复杂度为 \(O(n^2m)\)。
\(2.\) Floyd全源最短路径算法,时间复杂度为 \(O(n^3)\)。
\(3.\) Dijkstra单源最短路径算法,时间复杂度为 \(O(n^2)\),经过堆优化可达到 \(O(n log m)\)。求全源最短路径,枚举起点时间复杂度为 \(O(n^2logm)\)。
很明显,我们会选择第三种做法,这样的时间复杂度是最优的。
二.算法过程
Johnson提出了一种做法,就是按照模块一的第三种做法。
但是 Dijkstra 最短路径算法无法处理负边权,那怎么办呢?
下意识我们会将每个边权增加一个数字,但是这是错误的,因为这样会影响最短路径。
为了便于理解,这里给出oi-wiki的解释。
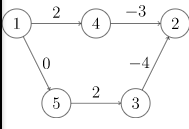
如下图,\(1->2\) 的最短路径是 \(1->5->3->2\),最短路径长度为 \(-2\)。
而当我们加上一个正整数 \(k\),如 \(5\),就会变成下图。
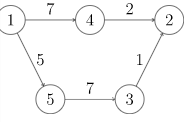
这时, \(1->2\) 的最短路径却是 \(1->4->2\)。
所以,这种做法会导致最短路径变化,所以是不可取的。
而 Johnson 算法提出了一种重新标注边权的方法:
我们建一个超级源点 \(0\),所有点与其连一条边权为 \(0\) 的边。
先采用 Spfa 算法将每个点与 超级源点 \(0\) 的最短路径长度算出来,这里记作 \(h_i\)。
那么,我们在跑 \(n\) 遍 Dijkstra 前,修改边权。
设一条有向边 \(u->v\) 边权为 \(w\),那么将每条边的边权增加 \(h_u-h_v\),当然,最后统计答案的时候要将其减去。
接下来以每个点为源点跑 \(n\) 遍 Dijkstra 求答案即可。
最初采用 Spfa 判断负环,是否有解,并不影响时间复杂度。
而最后跑 \(n\) 遍 Dijkstra 的时间复杂度为 \(O(n^2logm)\),该算法就可以比较高效的求全源最短路径了。
三.证明正确性
关于 Johnson 全源最短路算法,比较巧妙的就是将每条边权调整为非负。
至于为什么加这个数字呢?
这里设一条有向边 \(u->v\) 边权为 \(w\),还有上文的 \(h_i\) 为每个点与超级源点 \(0\) 的最短路径长度。
那么,我们知道边权满足以下三角形不等式:
\(h_u + w ≥ h_v\)
将其变形为:
\(w - h_v + h_u≥ 0\)
那么这样,将 \(w\) 增加 \(h_u-h_v\),就能满足非负性。
注意,最后统计答案的时候需要将其减去。
四.模板代码
这道题就是 Johnson 全源最短路算法的模板题了。
示范代码如下:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <functional>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define int ll
const int N = 16666;
const int inf = 1e9;
struct Edge {
int nxt;
int to;
int w;
}e[N];
int head[N], edge_num = 0;
inline void add_edge (int x, int y, int z) {
e[++ edge_num].to = y;
e[edge_num].nxt = head[x];
e[edge_num].w = z;
head[x] = edge_num;
}
int n, m, indeg[N], inque[N];
int d[N];
inline bool SPFA (int s) {//SPFA判断负环。
for (int i = 1; i <= n; i ++) {
d[i] = inf;
}
memset (inque, false, sizeof (inque));
queue<int> qwq;
qwq.push(s);
d[s] = 0, inque[s] = true;
indeg[s] ++;
while (!qwq.empty()) {
int u = qwq.front();
qwq.pop();
inque[u] = false;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (d[v] > d[u] + e[i].w) {
d[v] = d[u] + e[i].w;
if (inque[v] == false) {
qwq.push (v);
inque[v] = true;
indeg[v] ++;
if (indeg[v] >= n + 1) {
return true;
}
}
}
}
}
return false;
}
int dis[N];
bool vis[N];
inline void Dij (int s) {//求单源最短路径。
for (int i = 1; i <= n; i ++) {
dis[i] = inf;
}
memset (vis, false, sizeof (vis));
priority_queue<pii, vector<pii>, greater<pii> > q;
dis[s] = 0;
q.push (make_pair(0, s));
while (!q.empty()) {
int u = q.top().second;
q.pop();
if (vis[u]) {
continue;
}
vis[u] = true;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (vis[v] == false) {
q.push (make_pair(dis[v], v));
}
}
}
}
}
signed main() {
scanf ("%lld%lld", &n, &m);
for (int i = 1, x, y, z; i <= m; i ++) {
scanf ("%lld%lld%lld", &x, &y, &z);
add_edge (x, y, z);
}
for (int i = 1; i <= n; i ++) {
add_edge (0, i, 0);
}
if (SPFA (0) == true) {
//出现负环无解。
printf ("-1");
return 0;
}
for (int i = 1; i <= n; i ++) {
for (int j = head[i]; j; j = e[j].nxt) {
int v = e[j].to;
e[j].w += d[i] - d[v]; //使边权满足非负性。
}
}
for (int i = 1; i <= n; i ++) {
Dij (i);
ll ans = 0;
for (int j = 1; j <= n; j ++) {
if (dis[j] == inf) {
ans += 1ll * inf * j;
}
else {
ans += 1ll * j * (dis[j] - d[i] + d[j]);//要将其减去。
}
}
printf ("%lld\n", ans);
}
return 0;
}
另外,该题还涉及到 \(2\) 道模板题目,如下:
P3385 【模板】负环
到此,您就学会了 Johnson 全源最短路算法。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号