「学习笔记」笛卡尔树
一.笛卡尔树的概念
笛卡尔树是一种二叉树，能帮助我们查询区间最值，第 \(k\) 极值。每一个节点都由两个值构成，分别为 \(key\) 和 \(value\) 。要求 \(key\) 值满足二叉查找树的性质， \(value\) 值满足堆的性质，如下图所示（源于维基百科）。
我们在上图可以发现，在这颗笛卡尔树中，以数组元素为 \(value\) 值，以数组下标为 \(key\) 值。
并且，上图的 \(key\) 值满足二叉查找树的性质， \(value\) 值满足小根堆的性质，这就是一颗笛卡尔树了。
附：
二叉查找树的性质有三条：
\(1.\) 左子树上所有节点的值都小于等于它的根节点的值。
\(2.\) 右子树上所有节点的值都大于等于它的根节点的值。
\(3.\) 左、右子树也为二叉查找树。
二.笛卡尔树的构建
首先，我们将 \(key\) 值从小到大进行排序，再逐个插入笛卡尔树中。那么，我们每次插入的元素必然在这颗笛卡尔树的右链的末端，因为我们的 \(key\) 值是从小到大排序的，那么按照二叉查找树的定义，每次插入的节点肯定要排在这颗树的右链上。
那么，我们每次进行插入的过程就如下：
我们从当前右链的底部从下到上遍历，一直比较当前节点 \(u\) 和右链节点上的 \(value\) 值，如果找到一个右链节点 \(v\)，构成 \(v_{value}<u_{value}\)，就将节点 \(u\) 插到节点 \(v\) 的右子节点上，那么原来节点 \(v\) 的右子树就变为节点 \(u\) 的左子树了。
下面给出一张摘自oi-wiki的图片供大家参考，红框部分为右链。
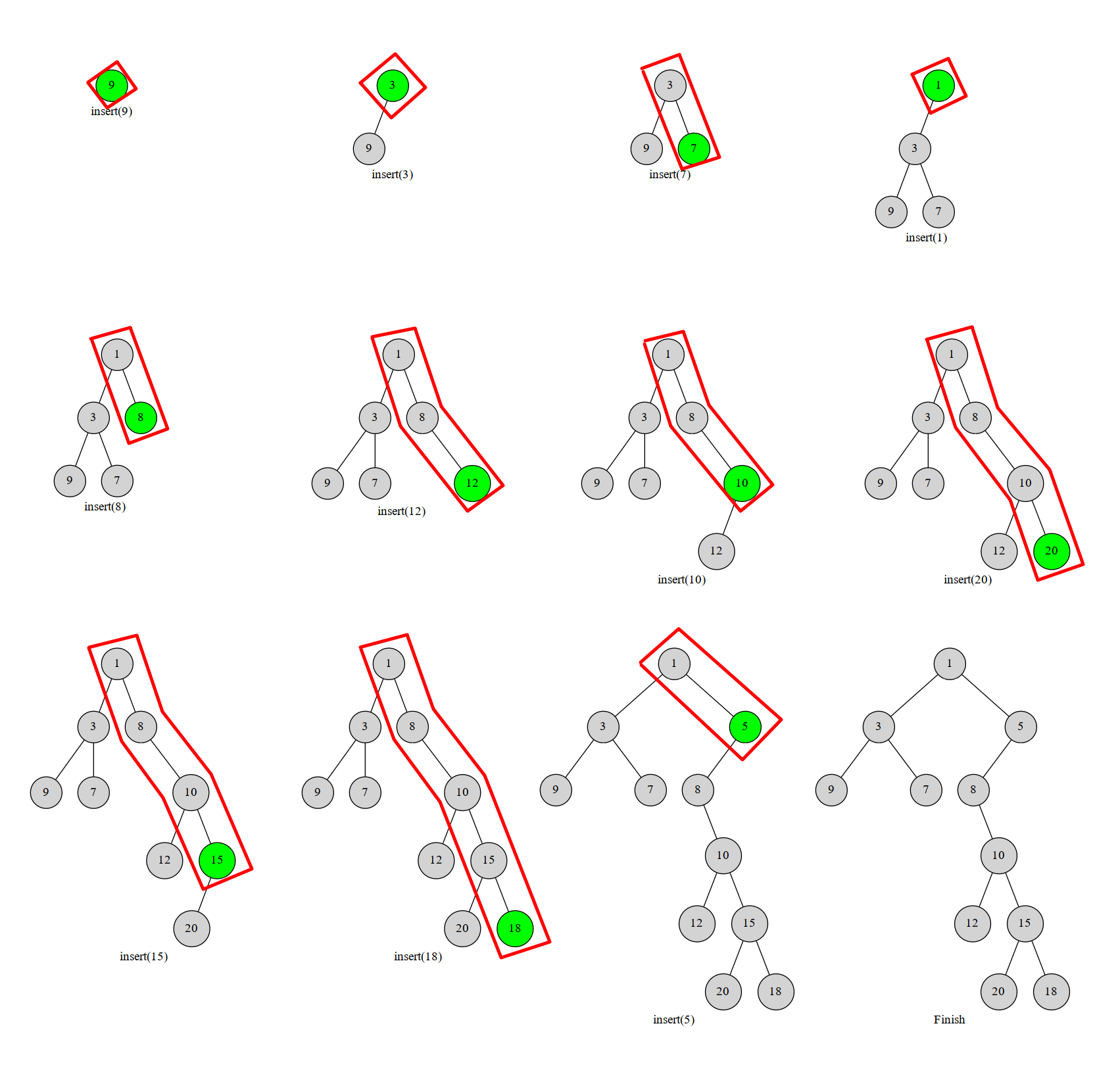
我们采用单调栈来维护右链。可以发现，每个点最多进出单调栈一次，也就是说，我们的时间复杂度是 \(O(N)\) 。
代码如下：
sta[1] = 1;
//以1为初始栈顶。
for (int i = 2; i <= n; i ++) {//ls为左子节点，rs为右子节点。
while (a[sta[top]] > a[i] && top) {
top --;
//弹栈，找与当前元素小于等于的元素。
}
if (!top) {
//如果右链上的节点都比当前元素小，那么当前节点就是右链的链顶。
ls[i] = sta[top + 1];
//那么原来的栈顶就是当前元素的左子节点。
}
else {
ls[i] = rs[sta[top]];
//将当前节点插入栈顶节点的下方，那么栈顶节点的左子节点就要变为当前节点的左子节点。
rs[sta[top]] = i;
// 当前节点就是栈顶节点的右子节点。
}
sta[++ top] = i;
//将key值入栈。
}
三.例题
例题 \(1\)：
这是笛卡尔树的模板题。
只要按照题目给出的排列 \(p\) 作为每个节点的 \(value\) 值建树，最后根据题目给出的两个公式计算答案即可。
核心代码与模块二的构建笛卡尔树代码相同，不放代码了。
例题 \(2\)：
依旧是比较模板的一道笛卡尔树题。
我们只要将题目给出的生成序列当做 \(key\) 值，把输入顺序当作 \(value\) 值就可以转换成模板题了。
最后，题目要求字典序最小，于是我们转化为先序遍历输出即可。
核心代码如下：
void dfs (int x) {
//先序遍历输出。
if (x) {
printf ("%d ", x);
dfs (ls[x]);
dfs (rs[x]);
}
}
for (int i = 1, x; i <= n; i ++) {
scanf ("%d", &x);
//将题目给定的生成序列当做key值。
a[x] = i;
//将输入顺序当做value值。
}
例题 \(3\)：
SP1805 HISTOGRA - Largest Rectangle in a Histogram
很经典的一道求最大矩阵的题目。
很显然，我们可以用笛卡尔树轻松完成。
我们可以先构建笛卡尔树，从根节点，也就是单调栈中的第一个节点开始遍历。
我们设一个为 节点 \(x\) 为根的子树大小为 \(siz_x\)，那么，我们只需要找到一个最大的 \((ls_{siz_i}+rs_{siz_i}+1)\) \(× h_i\) 就是最后的答案。
多测记得清空！！！
代码如下：
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 200005;
typedef long long ll;
int n, top = 1, ls[N], rs[N];
ll ans, siz[N], sta[N], a[N];
void dfs (ll x) {
if (ls[x]) {
dfs (ls[x]);
}
if (rs[x]) {
dfs (rs[x]);
}
siz[x] = siz[ls[x]] + siz[rs[x]] + 1;
ans = max (ans, siz[x] * a[x]);
}
int main() {
while (scanf ("%d", &n) != EOF && n) {
memset (a, 0, sizeof (a));
memset (siz, 0, sizeof (siz));
memset (ls, 0, sizeof (ls));
memset (rs, 0, sizeof (rs));
for (int i = 1; i <= n; i ++) {
scanf ("%d", &a[i]);
}
sta[1] = 1, ans = 0, top = 1;
for (int i = 2; i <= n; i ++) {
while (a[sta[top]] > a[i] && top) {
top --;
}
if (!top) {
ls[i] = sta[top + 1];
}
else {
ls[i] = rs[sta[top]];
rs[sta[top]] = i;
}
sta[++ top] = i;
}
dfs (sta[1]);
printf ("%lld\n", ans);
}
return 0;
}
四.参考资料
感谢以下作者，若有侵权请联系删除。
https://blog.csdn.net/weixin_34349320/article/details/93762012
