「学习笔记」二分图
零. 前言
作者为此学习笔记倾注了很大的精力,同时我给出了一个「练习题单」二分图供大家参考练习。如果有改进意见,可以随时提出。
一. 二分图定义
我们先来看看百度百科的定义
- 二分图又称作二部图,是图论中的一种特殊模型。 设\(G=(V,E)\)是一个无向图,如果顶点V可分割为两个互不相交的子集\((A,B)\),并且图中的每条边 \((i,j)\) 所关联的两个顶点i和j分别属于这两个不同的顶点集 (i \(\in\) A , j \(\in\) B),则称图G为一个二分图。
-------百度百科。
挺难理解的是不是。
我们结合图理解一下:
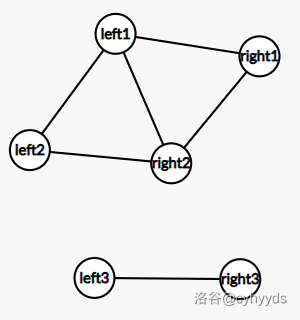
如图,在二分图中,能把点分成两个顶点集,使每一个顶点集中,没有两个点有连边,也就是说,边只会连接两个顶点集。
二. 二分图判定
我们有一个定理:当一个无向图为二分图时,图中不存在奇环。
我们一般采用染色法, \(dfs\) 遍历。
有三个步骤:
\(1.\) 初始化所有节点都未染色。
\(2.\) 从节点 \(u\) 出发进行染色为 \(c\) 。
\(3.\) 从节点 \(u\) 出发遍历所有与节点 \(u\) 有连接的点 \(v\),有三种情况:
-
节点 \(v\) 未染色,则将节点 \(v\) 染色为节点 \(u\) 的相反色。
-
节点 \(v\) 的颜色已是节点 \(u\) 的相反色,那继续第二步。
-
节点 \(v\) 和节点 \(u\) 的颜色相同,那么这个图就不是二分图。
这是一道判定二分图的题目,我们用染色法,最后二分答案即可。
代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int M = 1555555;
const int N = 25555;
struct EDGE {
int nxt;
int to;
int w;
}e[M];
int head[M], edge_num = 0, n, m;
inline void add_edge (int x, int y, int z) {
e[++edge_num].nxt = head[x];
e[edge_num].to = y;
e[edge_num].w = z;
head[x] = edge_num;
}
bool check (int mid) {
int col[N] = {};
queue<int> q;
for (int i = 1; i <= n; i ++) {
if (col[i] == 0) {//未染色
q.push(i);
col[i] = 1;
while (!q.empty()) {
int u = q.front();//取队头
q.pop();//弹出队头
for (int i = head[u]; i; i= e[i].nxt) {
if (e[i].w >= mid) {//仅保留边权大于mid的边
int v = e[i].to;
if (col[v] == 0) {//未染色
q.push(v);//入队
if (col[u] == 1) {
col[v] = 2;//染相反色
}
else {
col[v] = 1;//染相反色
}
}
else if (col[v] == col[u]) {
return false;//相同则不是二分图
}
}
}
}
}
}
return true;
}
int main() {
scanf ("%d%d", &n, &m);
int L = 0, R = 0;
for (int i = 1; i <= m; i ++) {
int x, y, z;
scanf ("%d%d%d", &x, &y, &z);
R = max (R, z);//右端点取最大边权
add_edge (x, y, z);
add_edge (y, x, z);//建双向边
}
R ++;
while (L + 1 < R) {//二分答案
int mid = L + R >> 1;
if (check(mid) == true) {
R = mid;
}
else {
L = mid;
}
}
printf ("%d", L);//要求答案最小化,输出左端点
return 0;
}
三. 二分图最大匹配
什么是二分图的匹配?
匹配是一个边的集合,且任意两条边都没有公共顶点。

这样就是一种匹配,匹配数就是 \(3\) 。
那如下图,这就不是一种匹配。
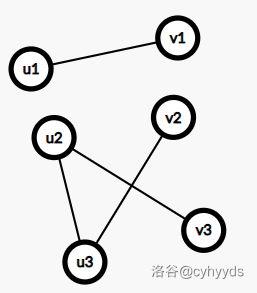
由于匹配很多,所以我们求的就是二分图最大匹配。
这两道是同一个模板。
在求最大匹配时,我们通常会使用匈牙利算法。(因为好写)
判定定理:
二分图的一组匹配 \(S\) 是最大匹配,当且仅当图中不存在 \(S\) 的增广路。
匈牙利算法就是一个不断找增广路的算法。
算法过程:
\(1.\) 设匹配 \(S\) 为空集合,也就是说与所有边都不匹配。
\(2.\) 枚举左部的一个点 \(u\) ,与其连接的右部点 \(v\) 尝试匹配,当满足下列两个条件中的一个时,匹配成功。
-
\(v\) 点未匹配过。
-
\(v\) 点已经和另外一个 \(v_j\) 点匹配,但是从 \(v_j\) 点出发还能找到可以匹配的点。
\(3.\) 一直重复第二步,直到找不到增广路了为止。
代码如下:
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1555555;
struct EDGE {
int nxt;
int to;
}e[N];
int head[N], edge_num = 0;
inline void add_edge (int x, int y) {
e[++edge_num].nxt = head[x];
e[edge_num].to = y;
head[x] = edge_num;
}
bool vis[N];
//vis[i]表示i点试图更改匹配成功或失败
int obj[N];
//obj[i]表示i点的匹配对象
int n, m, ie;
bool Hungary (int u) {
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (vis[v] == false) {//该点没有试图更改匹配
vis[v] = true;//标记该点试图更改匹配
if (obj[v] == 0 || Hungary(obj[v]) == true) {
//两个条件满足一个即可
obj[v] = u;
//v的匹配对象是u
return true;
//返回u点有匹配对象
}
}
}
return false;
//返回u点无匹配对象
}
int main() {
scanf ("%d%d%d", &n, &m, &ie);
for (int i = 1; i <= ie; i ++) {
int x, y;
scanf ("%d%d", &x, &y);
add_edge (x, y);
}
int cnt = 0;
for (int i = 1; i <= n; i ++) {
memset (vis, false, sizeof (vis));//每次更新vis
if (Hungary(i) == true) {
//i点有匹配则++
cnt ++;
}
}
printf ("%d", cnt);
return 0;
}
初看一头雾水,认真一看,这其实是一道裸的二分图最大匹配。
我们可以把每一个点看作二分图中的点,把它的行和列连边,就会发现这个图是一个匹配。
在两个操作中交换行列也相当于匈牙利算法中的协商调整,不影响最大匹配。
如果有 \(n\) 个及以上个匹配,那么就可以完成题目中的任务。
注意
此题多测,记得清空。(多测不清空,爆零两行泪。)
代码如下:
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 255;
int p[N][N], obj[N], n;
//obj为匹配对象
bool vis[N];
bool Hungary (int x) {//最大匹配
for (int i = 1; i <= n; i ++) {
if (p[x][i] == true && vis[i] == false) {
vis[i] = true;
if (obj[i] == 0 || Hungary(obj[i]) == true) {
obj[i] = x;
return true;
}
}
}
return false;
}
int main() {
int T;
cin >> T;
while (T --) {
memset (p, 0, sizeof (p));//多测清空操作
memset (obj, 0, sizeof (obj));//同上
cin >> n;
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
cin >> p[i][j];
}
}
int cnt = 0;
for (int i = 1; i <= n; i ++) {
memset (vis, false, sizeof (vis));
if (Hungary(i) == true) {
cnt ++;
}
}
if (cnt >= n) {
puts ("Yes");//大于等于n就可以实现题意
}
else {
puts ("No");
}
}
return 0;
}
很明显,这道题求最大匹配。
还需要输出配对方案,于是我们只要遍历一遍,寻找有匹配的输出即可。
代码如下:
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int N = 155555;
struct EDGE {
int nxt;
int to;
}e[N];
int obj[N], head[N], edge_num = 0;
inline void add_edge (int x, int y) {
e[++edge_num].to = y;
e[edge_num].nxt = head[x];
head[x] = edge_num;
}
bool vis[N];
bool Hungary(int u) {
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (vis[v] == false) {
vis[v] = true;
if (obj[v] == 0 || Hungary(obj[v]) == true) {
obj[v] = u;
return true;
}
}
}
return false;
}
int main() {
int m, n;
scanf ("%d%d", &m, &n);
int u, v;
while (1) {
scanf ("%d%d", &u, &v);
if (u == -1 && v == -1) {
break;
}
add_edge (u, v);
}
int cnt = 0;
for (int i = 1; i <= n; i ++) {
memset (vis, false, sizeof (vis));
if (Hungary(i) == true) {
cnt ++;
}
}
printf ("%d\n", cnt);
for (int i = m; i <= n; i ++) {
if (obj[i]) {
printf ("%d %d\n", obj[i], i);
}
}
return 0;
}
一道稍微需要变化思维的一道题,代码实现依旧简短,我们只要求最大匹配即可。
我们将两个属性值分别与编号 \(i\) 连边,最后求最大匹配时,由于答案在 \(1\) 到 \(10000\) 之间,所以最后累计答案也在其中。
有一个小常数优化:每次进行匈牙利算法时都 \(memset\) ,这样的常数过高。我们可以用一个时间戳来判断是否该点遍历过,可以大大优化我们的常数。
代码如下:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 3e6 + 5;
struct EDGE {
int nxt;
int to;
}e[N<<1];
int sjc = 0, n, head[N<<1], edge_num = 0, obj[N];
int vis[N<<1];
inline void add_edge (int x, int y) {
e[++edge_num].nxt = head[x];
e[edge_num].to = y;
head[x] = edge_num;
}
bool Hungary (int u) {
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (vis[v]!=sjc) {//时间戳
vis[v] = sjc;
if (obj[v] == -1 || Hungary(obj[v]) == true) {
obj[v] = u;
return true;
}
}
}
return false;
}
int main() {
memset (obj, -1, sizeof (obj));
scanf ("%d", &n);
for (int i = 1; i <= n; i ++) {
int x, y;
scanf ("%d%d", &x, &y);
add_edge (x, i);
add_edge (y, i);
}
int cnt = 0;
for (int i = 1; i <= 10000; i ++) {
sjc ++;//时间戳
if (Hungary(i) == true) {
cnt ++;
}
else {
break;
}
}
printf ("%d", cnt);
return 0;
}
P1894 [USACO4.2]完美的牛栏The Perfect Stall
一道裸的二分图最大匹配,直接匈牙利加邻接矩阵即可。
代码如下:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 555;
int obj[N], n, m;
bool vis[N], f[N][N];
bool Hungary (int u) {
for (int i = 1; i <= n; i ++) {
if (!vis[i] && f[u][i]) {
vis[i] = true;
if (obj[i] == 0 || Hungary(obj[i]) == true) {
obj[i] = u;
return true;
}
}
}
return false;
}
int main() {
scanf ("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) {
int x;
scanf ("%d", &x);
for (int j = 1; j <= x; j ++) {
int t;
scanf ("%d", &t);
f[t][i] = true;
}
}
int cnt = 0;
for (int i = 1; i <= n; i ++) {
memset (vis, false, sizeof (vis));
if (Hungary(i) == true) {
cnt ++;
}
}
printf ("%d", cnt);
return 0;
}
这道题依然是裸的二分图最大匹配,但是该题的建边方式有所不同。由于一排可以坐两个位置,所以我们要每排建边两次。
代码如下:
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 22222;
int obj[N];
bool vis[N];
struct EDGE {
int nxt;
int to;
}e[N];
int head[N], edge_num = 0;
inline void add_edge (int x, int y) {
e[++edge_num].nxt = head[x];
e[edge_num].to = y;
head[x] = edge_num;
}
bool Hungary (int u) {
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (!vis[v]) {
vis[v] = true;
if (obj[v] == 0 || Hungary (obj[v]) == true) {
obj[v] = u;
return true;
}
}
}
return false;
}
int main() {
int n;
scanf ("%d", &n);
for (int i = 1; i <= (n<<1); i ++) {
int x, y;
scanf ("%d%d", &x, &y);
add_edge (i, x);
add_edge (i, y);
add_edge (i, x+n);
add_edge (i, y+n);
//特殊建边
}
int cnt = 0;
for (int i = 1; i <= (n<<1); i ++) {
memset (vis, false, sizeof (vis));
if (Hungary(i) == true) {
cnt ++;
}
}
printf ("%d", cnt);
return 0;
}
四.二分图最小路径覆盖
什么是路径覆盖?题目给出了定义。
- 给定有向图 \(G=(V,E)\)。设 \(P\) 是 \(G\) 的一个简单路(顶点不相交)的集合。如果 \(V\) 中每个定点恰好在 \(P\) 的一条路上,则称 \(P\) 是 \(G\) 的一个路径覆盖。\(P\) 中路径可以从 \(V\) 的任何一个定点开始,长度也是任意的,特别地,可以为 \(0\)。 \(G\) 的最小路径覆盖是 \(G\) 所含路径条数最少的路径覆盖。
在这里,有一个很重要的结论。
最小路径覆盖 = 顶点数 - 最大匹配数。
为什么呢?
设图 \(G\) 有 \(n\) 个点。
当点之间没有边时,路径数等于点数,也就是 \(n-0\)。
当多出来一条匹配边 \(x->y\) 时,因为 \(x\) 和 \(y\) 在同一条边上,所以路径数减一,也就是 \(n - 1\)。
以此类推,我们可以得到:最小路径覆盖 = 顶点数 - 最大匹配数。
当然这还没完,在此题中,要求我们输出路径。
我们这就需要一个拆点的思想,将每个点 \(u_i\) 拆成 \(u_i\) 和 \(u_{i+n}\) ,建立一个新的二分图。
于是,左部点就是 \(1\) ~ \(n\) ,右部点就是 \(n+1\) ~ \(2n\)。这样,我们就得到了一个新的拆点二分图。
代码如下:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 15555;
struct GAP {
int nxt;
int to;
}e[N];
int head[N], edge_num = 0, n, m;
inline void add_edge (int x,int y) {
e[++edge_num].nxt = head[x];
e[edge_num].to = y;
head[x] = edge_num;
}
bool vis[N];
int obj[N];
bool Hungary (int u) { //匈牙利算法求最大匹配
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (vis[v] == false) {
vis[v] = true;
if (obj[v] == 0 || Hungary(obj[v]) == true) {
obj[v] = u;
obj[u] = v;
return true;
}
}
}
return false;
}
inline void print (int x) {
x += n;//加n使点x为右部点
do {
printf ("%d ", x - n);//减回去
vis[x - n] = true;//记录
x = obj[x - n];//使x点成为下一个路径上的点
}while (x);
puts (" ");//换行
}
int main() {
scanf ("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int u, v;
scanf ("%d%d", &u, &v);
add_edge (u, v + n); //拆点
}
int cnt = 0;
for (int i = 1; i <= n; i ++) {
memset (vis, false, sizeof (vis));//每次都要更新
if (Hungary(i) == true) {
cnt ++;
}
}
for (int i = 1; i <= n; i++) {
if (vis[i] == false) {//输出路径
print (i);
}
}
printf ("%d", n - cnt);//运用定理
return 0;
}
同样,这题也是一道很经典的最小路径覆盖问题。
我们使用上题的定理:最小路径覆盖 = 顶点数 - 最大匹配数。
直接用匈牙利算法计算最大匹配即可。
注意
该题多测,注意清空。
代码如下:
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1555555;
struct EDGE {
int nxt;
int to;
}e[N];
int obj[N], head[N], edge_num = 0, n, m, T;
inline void add_edge (int x, int y) {
e[++edge_num].nxt = head[x];
e[edge_num].to = y;
head[x] = edge_num;
}
bool vis[N];
bool Hungary (int u) {
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (vis[v] == false) {
vis[v] = true;
if (obj[v] == 0 || Hungary(obj[v]) == true) {
obj[v] = u;
return true;
}
}
}
return false;
}
inline void init () {
memset (vis, false, sizeof (vis));
memset (obj, 0, sizeof (obj));
memset (head, 0, sizeof (head));
edge_num = 0;
}
int main() {
scanf ("%d", &T);
while (T--) {
init();//多测清空
scanf ("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int u, v;
scanf ("%d%d", &u, &v);
add_edge (u, v);
}
int cnt = 0;
for (int i = 1; i <= n; i ++) {
memset (vis, false, sizeof (vis));
if (Hungary(i) == true) {
cnt ++;//匈牙利求最大匹配
}
}
printf ("%d\n", n - cnt);
}
}
//样例噢
/*
2
4
3
3 4
1 3
2 3
3
3
1 3
1 2
2 3
ans:
2
1
*/
五. 二分图最小点覆盖
- 点覆盖,在图论中点覆盖的概念定义如下:对于图 \(G=(V,E)\)中的一个点覆盖是一个集合 \(S⊆V\) 使得每一条边至少有一个端点在 \(S\) 中。 --百度百科
通俗的来说,也就是一条路径使图 \(G\) 的每条边的至少一个顶点都在该路径的某个点上。
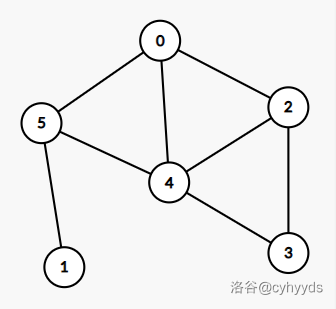
如上图,最小点覆盖就是 \(5->4->2\)。
有一个定理需要记住:
最小点覆盖 = 最大匹配数
我们将 \(a_i\) 与 \(b_i\) 连边跑最小点覆盖即可。
这道题就是很典型的求二分图最小点覆盖。
\(n\) 的范围极小,我们用邻接矩阵存储即可。
最大匹配用匈牙利算法即可,这道题就迎刃而解了。
代码如下:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 666;
int n, m, obj[N];
bool vis[N], g[N][N];
bool Hungary (int u) {
for (int i = 1; i <= n; i ++) {
if (vis[i] || !g[u][i]) {
continue;
}
vis[i] = true;
if (obj[i] == 0 || Hungary (obj[i]) == true) {
obj[i] = u;
return true;
}
}
return false;
}
int main() {
scanf ("%d%d", &n, &m);
for (int i = 1; i <= m; i ++) {
int x, y;
scanf ("%d%d", &x, &y);
g[x][y] = true;
}
int cnt = 0;
for (int i = 1;i <= n; i ++) {
memset (vis, false, sizeof (vis));
if (Hungary(i) == true) {
cnt ++;
}
}
printf ("%d", cnt);
return 0;
}
六.二分图最大独立集
独立集:对于一张无向图 \((V,E)\) ,若存在一个点集 \(V′\),满足 \(V′⊆V\) ,且对于任意 \(u,v∈V′\),\((u,v)∉E\),则称 \(V′\) 为这张无向图的一组独立集。
最大独立集:包含点数最多的独立集被称为图的最大独立集。
定理:
最大独立集=点数-最小点覆盖=点数-最大匹配数
题目要求选择一些点,使这些点不能互相攻击。
我们将不能一起放置的点连边,那么答案就是最大独立集。
接下来我们要将这些点分为两个点集,观察题目,发现列 \(-1,+1,-3,+3\),那么可以按照列的奇偶性建图,分为两个点集即可。
建图代码如下:
int f (int x, int y) {
return (x - 1) * m + y;
}
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= m; j ++) {
if (!(i & 1)) {//找偶数列
if (!a[i][j]) {//没有障碍
for (int k = 0; k < 8; k ++) {
int nx = i + dx[k];
int ny = j + dy[k];
if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && !a[nx][ny]) {
add (f (i, j), f (nx, ny));
//f (i,j) 是偶数列
//f (nx, ny) 是奇数列
}
}
}
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号