2019软件工程实践第三次作业
一、GitHub地址:
地址如下:https://github.com/darkness-li/031702430
二、PSP表格:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | 40 |
| Estimate | 估计这个任务需要多少时间 | 2050 | 2440 |
| Development | 开发 | 240 | 300 |
| Analysis | 需求分析 (包括学习新技术) | 240 | 220 |
| Design Spec | 生成设计文档 | 100 | 130 |
| Design Review | 设计复审 | 120 | 150 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 60 | 100 |
| Design | 具体设计 | 120 | 150 |
| Coding | 具体编码 | 240 | 300 |
| Code Review | 代码复审 | 180 | 200 |
| Test | 测试(自我测试,修改代码,提交修改) | 120 | 180 |
| Reporting | 报告 | 240 | 300 |
| Test Repor | 测试报告 | 180 | 200 |
| Size Measurement | 计算工作量 | 30 | 40 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 120 | 150 |
| 合计 | 2050 | 2440 |
三、解题思路描述:
在刚拿到这个题目的时候,第一眼的印象是要求好多啊(哈哈哈)。由于以前没有玩过数独,所以我就先去了解了一下数独的规则,传统的数独游戏一般是9宫格,但这次作业的要求确是3到9宫格,所以刚开始还是有点吓到的。以下是我在解决这个问题的过程中的分析过程:
1.初步分析:
刚开始分析时,我认为结合宫格的行、列和每个小宫中的数字信息应该就能确定出未填空格要填入什么数字,而且题目也说了输入仅保证只有一个解,所以我认为在遍历完一遍整个数独之后应该至少能填入一个空,而当填了一个空之后,我们已知的信息就又多了,再多遍历几遍应该就能填完整个数独。在这个阶段的我,觉得出题人是不是有点sha,明明这么简单的题,而后面证明了是我太天真了。
2.碰壁阶段:
在按照初步分析的思路后,我迫不及待地下手写了第一个代码。而且,助教给的用例还成功跑完了3-6阶的宫格,但是在跑7阶和8阶的宫格时,我的程序奔溃了。。。(o(╥﹏╥)o......)因为执行完程序之后output.txt文件里根本没有内容,而且命令行也直接卡死了。所以,我就知道了肯定有bug。。在看了一下7宫格的数独后,我发现了我初步想法里的一个致命的问题,那就是有时候并不是遍历完一遍数独之后一定能填入一个空,因为有时候多个待填入的空里都存在着多种可能,需要我们去假设推理、去试探才能解出题来,所以,意识到这个bug之后,我简直要气炸了,这意味着我这个代码GG了。
3.深入分析:
在发现bug之后,在悲伤了一段时间之后,我知道还是要面对现实。通过分析之前的错误,我知道有时候数独里的空并不是仅根据宫格的行、列和每个小宫中的数字信息就能确定的,还需要我们先假设一个空,然后根据这个假设去填下一个空,当有一个空没办法填的时候,说明我们上一步假设错了,上一步应该填另外一个数字。依据此过程,直到填出整个数独为止。按这样的分析,我觉得这应该是个采用深度优先搜索策略的题目,也意味着我必须再修改程序。但是,可能是出于对第一个失败代码的眷恋,我认为其实也不必从第一个空开始就采用深度优先搜索,因为有些数独是仅仅根据行列宫的信息就能解出来的。因此,最终我决定这样修改我的程序:先按照初步分析阶段的设想,先把仅根据行列宫就能唯一确定的空先填入,如果最后成功填出整个数独,说明我们就不用进行深度优先搜索;如果最后不能成功填出整个数独,则说明我们要采用深度优先搜索策略,但此时因为我们已经或多或少地填了一些空格,那样就可以减少深搜的时间了。
四、设计实现过程:
在设计实现时,因为我发现3-9宫这7个宫格有些宫格具有共性,而有些具有特性,所以我认为可以将这7个宫格分为三类:第一类,3、5、7阶宫格,因为这些宫格不需要考虑宫的信息;第二类,4、9阶宫格,这些宫格虽然要考虑宫的信息,但是小宫的形状是规则的;第三类,6、8阶宫格,每个小宫的形状不规则。但是,这样分类可能导致我写的模块有点多,应该也可以把他们综合起来考虑,从而使整个程序看起来更精简。以下是我程序中主要的函数模块:
1.void sudok1(int m, int count);//参数m为宫格的阶数,count为待填入的空格总数;
功能:sudok1函数的功能是先把阶数为3、5、7的数独中仅根据行列信息就能唯一确定的数字填入
2.void sudok2(int m, int count);//参数m为宫格的阶数,count为待填入的空格总数;
功能:sudok2函数的功能是先把阶数为4、9的数独中仅根据行、列、小宫的信息就能唯一确定的数字填入
3.void sudok3(int m, int count); //参数m为宫格的阶数,count为待填入的空格总数;
功能:sudok3函数的功能是先把阶数为6、8的数独中仅根据行、列、小宫的信息就能唯一确定的数字填入
ps:这三个子函数也是我按照初步分析所写的第一个代码的主要内容,在最终考量后,我决定也将这些函数作为一些功能模块来使用,所以就保留了它们。
4.int dfs(int n, int m);//深搜函数是这个程序的核心部分,这里先把数独的每个位置从1-n*n编号,n的初值为一,即数独最左上的位置;参数m代表数独的阶数
功能:深度优先搜索函数,对于数独中每个位置为0的格,从1-m(m为阶数)这m个数中先检查哪个数能填入数独,若能填入则填入,当把整个数独的每个空位都成功填入一次后,说明我们解出了这个数独,于是返回;如果这m个数中没有一个满足要求,则回溯,并将填入的数字置0。
5.int check1(int x, int y, int m, int num);//x为试填的空格的横坐标,y为试填的空格的纵坐标,m为宫格的阶数,num代表试图填入的数
功能:check1函数用于检查试填入阶数为3、5、7宫格的数字的合法性
6.int check2(int x, int y, int m, int num);//参数信息同上
功能:check2函数用于检查试填入阶数为4、9宫格的数字的合法性
7.int check3(int x, int y, int m, int num);//参数信息同上
功能:check3函数用于检查试填入阶数为6、8宫格的数字的合法性
子函数间的关系流程图如下:
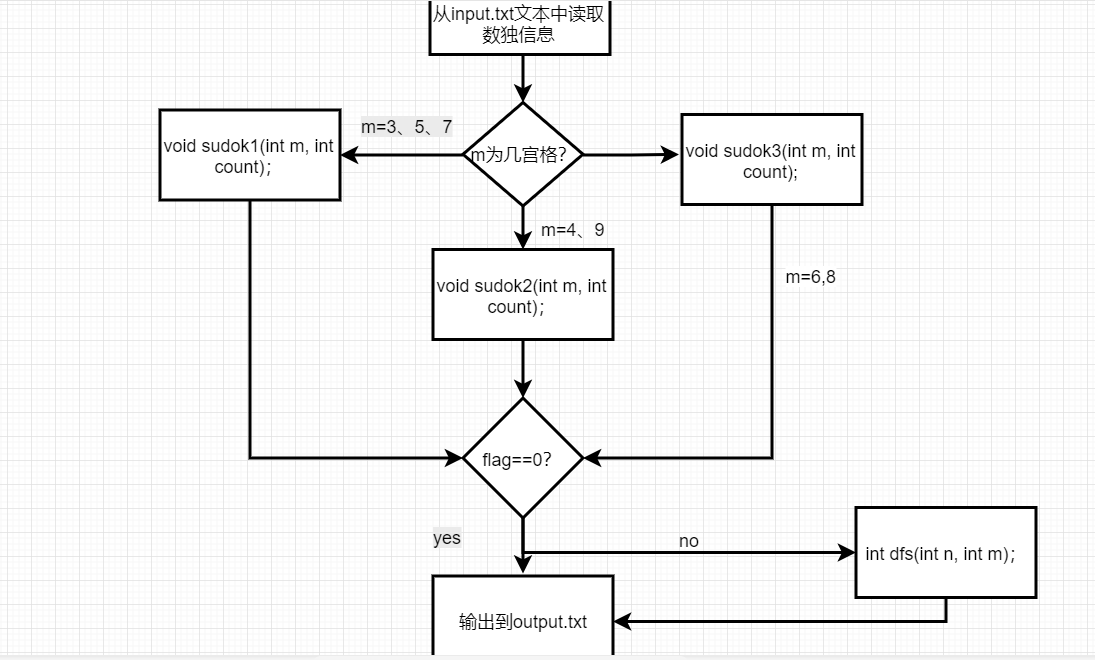
五、程序性能改进:
目前在程序性能改进上还没有过多的想法,现有的解决方法我只能想到深度优先搜索策略,如果说要朝哪些方向优化的话,我觉得可以考虑一下改进深度优先搜索所选取第一个空格的位置,可能位置选取的好的话,就可以更快地解出数独,减少回溯的次数。同时,对于有多个解的数独,如何把每一个解都罗列出来,这应该也是改进的一个方向!
六、用例测试:
1.未采用深度优先搜索策略,仅根据行列宫信息来确定所要填入的数字的代码:
先测试5宫格:

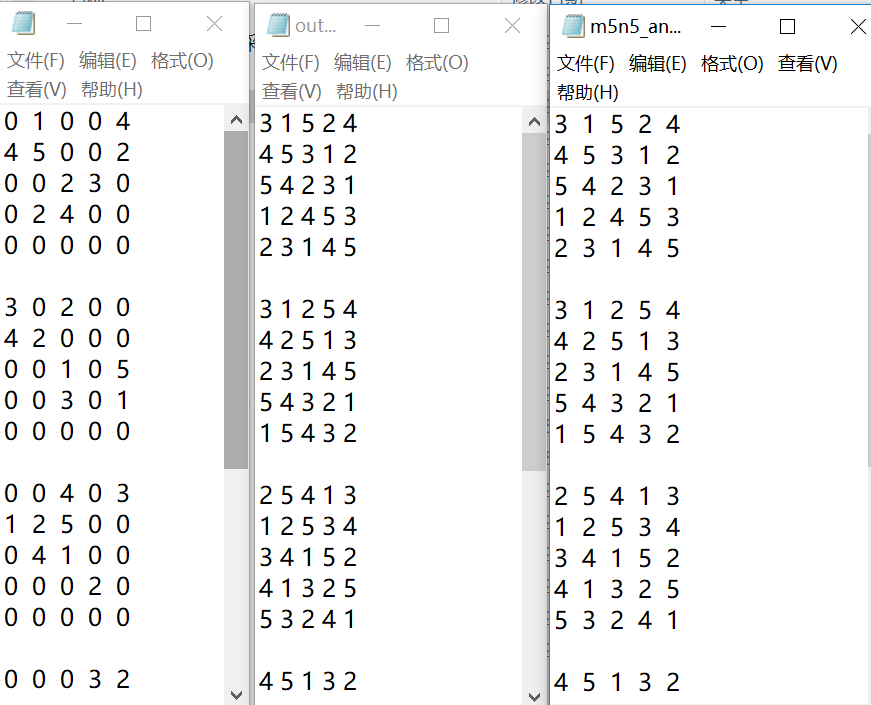
其实这个代码在测试部分数独时是能给出正确结果的,但是在测试7宫格时:

命令行就直接卡死了。。output.txt也没有输出,说明程序陷入了死循环,因此,对于某些数独,是有必要采用深度优先搜索策略的。
2.采用深度优先搜索策略,并结合第一个失败代码的测试用例:
(代码经过code quality analysis的检查结果为:)

3宫格(左边为input.txt,中间为output.txt,右边为答案文本):

4宫格:

5宫格:

6宫格:

7宫格:

8宫格:
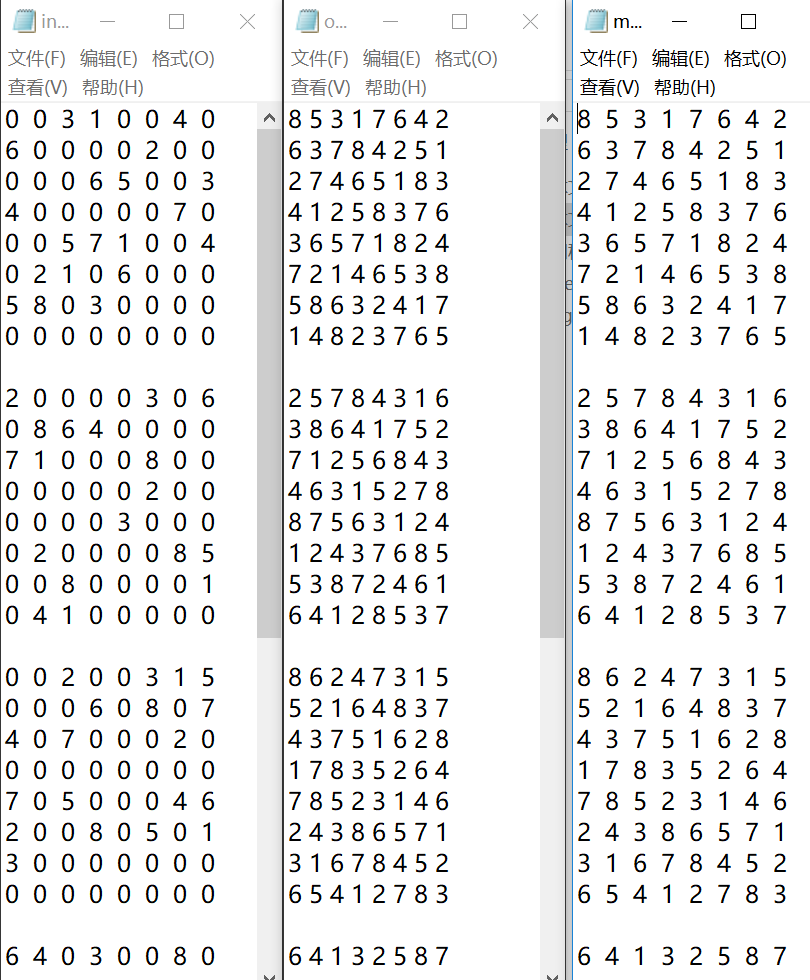
9宫格:
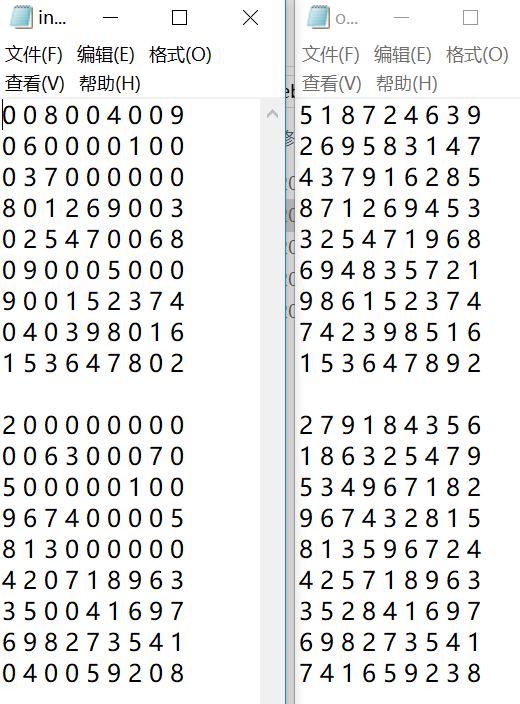
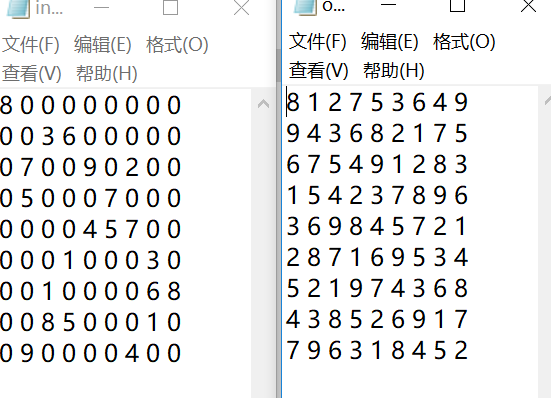
最后再加一道世界级难度的9宫格数独:
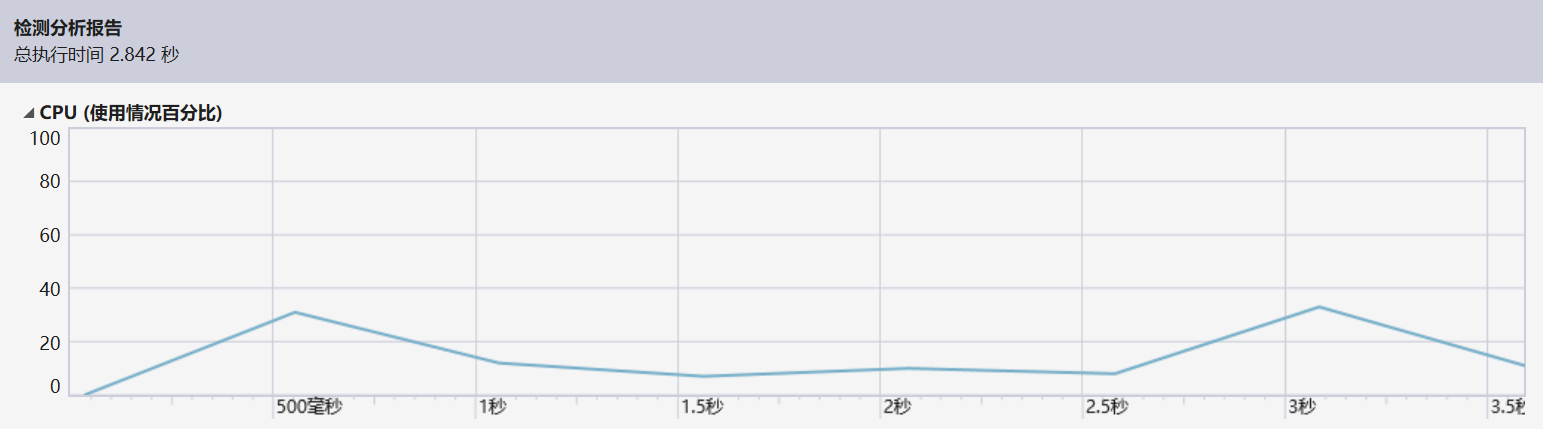
七:性能分析:
由于是第一次使用性能分析的工具,所以对这个工具的主要作用和内容还不是很理解,需要后续继续学习和掌握。以下是一些性能分析的截图:

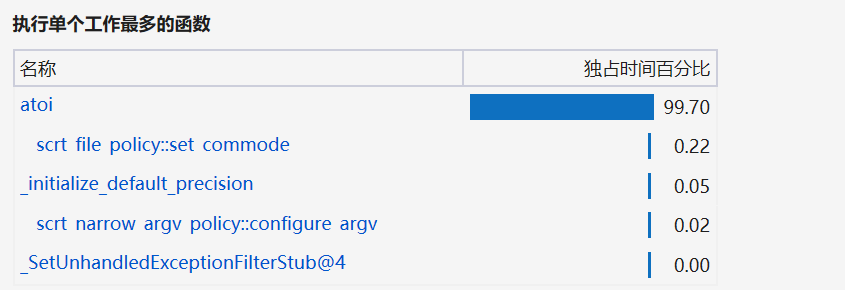

八、完整代码(Sudoku.cpp)如下:
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<fstream>
#include<cmath>
#pragma warning(disable:4996)
#include"stdafx.h"
using namespace std;
int s[10][10], s1[10][10];//数组s[10][10]用于保存从input.txt中读入的数独信息,s1[10][10]为备份的数独信息
int flag = 0, pan = 0;//定义两个起标志作用的循环变量,用于下面的程序使用
int check1(int x, int y, int m, int num) { //check1()函数用于检查填入阶数为3、5、7宫格的数字的合法性
int x1 = x, y1 = y, m1 = m, num1 = num;
int i;
for (i = 1; i <= m1; i++) {
if (s[x1][i] == num1) { //如果宫格的列中存在要填入的数字num,则不能填入,返回0
return 0;
}
}
for (i = 1; i <= m1; i++) {
if (s[i][y1] == num1) { //如果宫格的行中存在要填入的数字num,则不能填入,返回0
return 0;
}
}
return 1;
}
int check2(int x, int y, int m, int num) { //check2()函数用于检查填入阶数为4、9宫格的数字的合法性
int x1 = x, y1 = y, m1 = m, num1 = num;
int i, j, flag1, k;
int row, col;
k = (int)sqrt(m1);
flag1 = check1(x1, y1, m1, num1);
if (flag1 == 0) //调用check1函数先检查行列的合法性,不合法则直接返回0
return 0;
if (flag1 == 1) {
row = ((x1 - 1) / k * k) + 1;
col = ((y1 - 1) / k * k) + 1;
for (i = row; i < row + k; i++) {
for (j = col; j < col + k; j++) { //检查要填入的位置所在的小宫格的合法性
if (s[i][j] == num1) {
return 0;
}
}
}
}
return 1;
}
int check3(int x, int y, int m, int num) { //check3()函数用于检查填入阶数为6、8宫格的数字的合法性
int x1 = x, y1 = y, m1 = m, num1 = num;
int i, j, flag1;
int row, col;
flag1 = check1(x1, y1, m1, num1);
if (flag1 == 0) //调用check1函数先检查行列的合法性,不合法则直接返回0
return 0;
if (flag1 == 1) {
if (m1 == 6) {
row = ((x1 - 1) / 2 * 2) + 1;
col = ((y1 - 1) / 3 * 3) + 1; //这是一个用于计算小宫格最左上的位置坐标的公式
x1 = 2; y1 = 3;
}
if (m1 == 8) {
row = ((x1 - 1) / 4 * 4) + 1;
col = ((y1 - 1) / 2 * 2) + 1;
x1 = 4; y1 = 2;
}
for (i = row; i < row + x1; i++) {
for (j = col; j < col + y1; j++) { //检查要填入的位置所在的小宫格的合法性
if (s[i][j] == num) {
return 0;
}
}
}
}
return 1;
}
int dfs(int n, int m) { /*深度优先搜索函数,对于数独中每个位置为0的格,从1-m(m为阶数)这m个数中先检查哪个数能填入数独,若能填入则填入,当把整个数独
的每个空位都成功填入一次后,说明我们解出了这个数独,于是返回;如果这m个数中没有一个满足要求,则回溯,并将填入的数字置0。*/
int i;
if (n > m*m) {
pan = 1;
return 0;
}
if (s[((n - 1) / m) + 1][((n - 1) % m) + 1] != 0) { //这里把数独的每个位置从1-n*n编号,((n - 1) / m) + 1用于计算位置的行坐标,((n - 1) % m) + 1用于计算位置的列坐标
dfs(n + 1, m);
}
if (s[((n - 1) / m) + 1][((n - 1) % m) + 1] == 0) {
for (i = 1; i <= m; i++) { //检查1-m这m个数中哪几个数能填入
int flag = 0;
if (m == 3 || m == 5 || m == 7) {
flag = check1(((n - 1) / m) + 1, ((n - 1) % m) + 1, m, i);
}
if (m == 4 || m == 9) {
flag = check2(((n - 1) / m) + 1, ((n - 1) % m) + 1, m, i);
}
if (m == 6 || m == 8) {
flag = check3(((n - 1) / m) + 1, ((n - 1) % m) + 1, m, i);
}
if (flag == 1) {
s[((n - 1) / m) + 1][((n - 1) % m) + 1] = i; //flag=1说明该位置能填入i,则填入,继续搜索下一个格子
dfs(n + 1, m);
if (pan == 1)
return 0;
s[((n - 1) / m) + 1][((n - 1) % m) + 1] = 0;//说明填入的数字不满足要求,将原先赋值的空位置0
}
}
}
return 0;
}
void sudok1(int m, int count) { //sudok1函数先把阶数为3、5、7的数独中仅根据行列信息就能唯一确定的数字填入
int i, j, k1, k2, k3;
int m1 = m;
int count1 = count;
int m2 = m1 + 1;
int count2;
while (count1) {
count2 = count1; //定义count2变量,在每次遍历整个数独之前,将count1的值赋给它
for (i = 1; i < m1 + 1; i++) {
for (j = 1; j < m1 + 1; j++) {
if (s[i][j] == 0) {
int count2 = m1;
int a[10] = { 0 };
for (k1 = 1; k1 < m1 + 1; k1++) {
if (s[i][k1] != 0) {
if (a[s[i][k1]] == 0) {
a[s[i][k1]] = 1;
count2--;
}
}
}
for (k2 = 1; k2 < m1 + 1; k2++) {
if (s[k2][j] != 0) {
if (a[s[k2][j]] == 0) {
a[s[k2][j]] = 1;
count2--;
}
}
}
if (count2 == 1) {
count1--; //当找到一个能填入的数时,count1变量减一
for (k3 = 1; k3 < m1 + 1; k3++) {
if (a[k3] == 0) {
s1[i][j] = k3;
s[i][j] = k3;
break;
}
}
}
}
}
}
if (count2 == count1) { //在遍历完整个数独之后,如果count1变量的值没有改变,说明这轮遍历找不到能填的数了,就退出循环
flag = 1;
break;
}
}
}
void sudok2(int m, int count) { //sudok2函数先把阶数为4、9的数独中仅根据行、列、小宫的信息就能唯一确定的数字填入
int i, j, k, k1, k2, k3, m2;
int row;//行
int col;//列
int m1 = m;
int count1 = count;
k = (int)sqrt(m1);
m2 = m1 + 1;
int count3;
while (count1) {
count3 = count1;
for (i = 1; i < m1 + 1; i++) {
for (j = 1; j < m1 + 1; j++) {
if (s[i][j] == 0) {
int count2 = m1;
int a[10] = { 0 };
for (k1 = 1; k1 < m1 + 1; k1++) {
if (s[i][k1] != 0) {
if (a[s[i][k1]] == 0) {
a[s[i][k1]] = 1;
count2--;
}
}
}
for (k2 = 1; k2 < m1 + 1; k2++) {
if (s[k2][j] != 0) {
if (a[s[k2][j]] == 0) {
a[s[k2][j]] = 1;
count2--;
}
}
}
row = ((i - 1) / k * k) + 1; //计算小宫格最左上位置的横坐标
col = ((j - 1) / k * k) + 1; //计算小宫格最左上位置的纵坐标
for (k1 = row; k1 < row + k; k1++) {
for (k2 = col; k2 < col + k; k2++) {
if (s[k1][k2] != 0) {
if (a[s[k1][k2]] == 0) {
a[s[k1][k2]] = 1;
count2--;
}
}
}
}
if (count2 == 1) {
count1--;
for (k3 = 1; k3 < m1 + 1; k3++) {
if (a[k3] == 0) {
s1[i][j] = k3;
s[i][j] = k3;
break;
}
}
}
}
}
}
if (count3 == count1) {
flag = 1;
break;
}
}
}
void sudok3(int m, int count) { //sudok3函数先把阶数为6、8的数独中仅根据行、列、小宫的信息就能唯一确定的数字填入
int i, j, x1, y1, k1, k2, k3;
int row;//行
int col;//列
int m1 = m;
int count1 = count;
int m2 = m1 + 1;
int c;
int count3;
while (count1) {
count3 = count1;
for (i = 1; i < m1 + 1; i++) {
for (j = 1; j < m1 + 1; j++) {
if (s[i][j] == 0) {
int count2 = m1;
int a[10] = { 0 };
for (k1 = 1; k1 < m1 + 1; k1++) {
if (s[i][k1] != 0) {
c = s[i][k1];
if (a[c] == 0) {
a[c] = 1;
count2--;
}
}
}
for (k2 = 1; k2 < m1 + 1; k2++) {
if (s[k2][j] != 0) {
if (a[s[k2][j]] == 0) {
a[s[k2][j]] = 1;
count2--;
}
}
}
if (m1 == 6) {
x1 = 2; y1 = 3;
row = ((i - 1) / x1 * x1) + 1; //计算小宫格最左上位置的横坐标
col = ((j - 1) / y1 * y1) + 1; //计算小宫格最左上位置的纵坐标
}
if (m1 == 8) {
x1 = 4; y1 = 2;
row = ((i - 1) / x1 * x1) + 1;
col = ((j - 1) / y1 * y1) + 1;
}
for (k1 = row; k1 < row + x1; k1++) {
for (k2 = col; k2 < col + y1; k2++) {
if (s[k1][k2] != 0) {
if (a[s[k1][k2]] == 0) {
a[s[k1][k2]] = 1;
count2--;
}
}
}
}
if (count2 == 1) {
count1--;
for (k3 = 1; k3 < m1 + 1; k3++) {
if (a[k3] == 0) {
s1[i][j] = k3;
s[i][j] = k3;
break;
}
}
}
}
}
}
if (count3 == count1) {
flag = 1;
break;
}
}
}
int main(int argc, char *argv[]) {
int n, m,k;//m是宫格阶级,n是盘面数目
int i, j, count;
FILE *fp1;
FILE *fp2;
m = atoi(argv[2]);//获取从命令行中输入的参数
n = atoi(argv[4]);
fp1 = fopen("input.txt", "r");
if (fp1 == NULL)
return -1;
fp2 = fopen("output.txt", "r");
if (fp2 == NULL)
return -1;
fclose(fp2);
while (n--) {
i = 0, j = 0, count = 0, flag = 0;//初始化循环变量
s[10][10] = { 0 };
s1[10][10] = { 0 };
for (i = 1; i < m + 1; i++) {
for (j = 1; j < m + 1; j++) {
fscanf(fp1, "%d", &s[i][j]);//从input.txt中读入数独的信息
s1[i][j] = s[i][j];
if (s1[i][j] == 0)
count++;
}
}
if (m == 3 || m == 5 || m == 7)
sudok1(m, count);
if (m == 4 || m == 9)
sudok2(m, count);
if (m == 6 || m == 8)
sudok3(m, count);
if (flag == 1) { //flag==1说明该数独不能仅根据行、列、小宫的信息完成填入,要执行dfs函数
k=dfs(1, m);
}
pan = 0; flag = 0;//处理完每组数独后对控制变量重新赋初值
fp2 = fopen("output.txt", "a");
if (fp2 == NULL)
return -1;
for (i = 1; i < m + 1; i++) {
for (j = 1; j < m + 1; j++) {
fprintf(fp2, "%d", s[i][j]);//将处理好的数独写入output.txt
if (j != m)
fprintf(fp2, " ");
}
fprintf(fp2, "\n");
}
fprintf(fp2, "\n");
fclose(fp2);
s[10][10] = { 0 }; //初始化数组
s1[10][10] = { 0 };
}
fclose(fp1);
return 0;
}
九、心路历程与收获:
这次的编程作业,是我第一次如此系统而又完整地接触到编写一个程序的过程,感觉这整个过程下来我确实学到了挺多的东西,例如GitHub的使用、visual studio 2107的使用、文件系统的使用以及如何从命令行传递参数到主程序中(当然还有到现在仍不太懂得使用的单元测试)。我觉得这次编程作业带给我的不仅仅是编程能力上的一些小提高,更重要的是让我明白了只有清晰地了解需求、系统地制定方案、严谨而又有序地执行计划、合理安排时间,才能够写出更高质量的程序。总体而言,虽然过程痛苦,但是受益匪浅!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号