KMP注记
相关介绍在下面:
- https://blog.csdn.net/yutianzuijin/article/details/11954939
- http://www.cnblogs.com/dolphin0520/archive/2011/08/24/2151846.html
实际上,最先看的是2,但并描述没那么清晰,1上的图描述易于理解。这里保存一下。注释见图注。
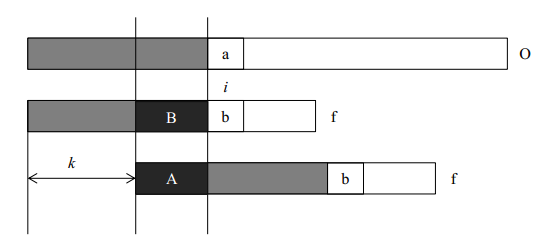 Fig 1. `O`是待搜索串,`f`是模式串。如果在`i`处没有匹配上,可以已知在该处之前有一定长度的后缀与O对应上(就是B段),所以如果有`next`表的协助,可以知道将f后移多少(就是*k*),能够匹配上这段后缀对应上O的字段。
Fig 1. `O`是待搜索串,`f`是模式串。如果在`i`处没有匹配上,可以已知在该处之前有一定长度的后缀与O对应上(就是B段),所以如果有`next`表的协助,可以知道将f后移多少(就是*k*),能够匹配上这段后缀对应上O的字段。
def genNext(s, nextTab=None, idx=0):
assert idx>=0, idx
if nextTab is None:
nextTab = [0 for i in s]
if idx==len(nextTab):
return nextTab
if idx ==0:
nextTab[idx] = -1
# fill the idx-th element...
else:
if s[nextTab[idx-1]+1] == s[idx]:
nextTab[idx] = nextTab[idx-1] +1
else:
nextTab[idx] = 0
return genNext(s,nextTab, idx+1)
s='ababcababa'
p='ababa'
print s
print p
print genNext(p)
def searchPat(s,p):
nextTab = genNext(p)
j=0
i=0
while True:
if s[i]==p[j]:
j+=1
i+=1
elif nextTab[j] >=0:
j=nextTab[j]
elif nextTab[j]==-1:
i += 1
j = 0
# print i,j
if j==len(p):
return i-j
return -1
print searchPat(s,p)



【推荐】还在用 ECharts 开发大屏?试试这款永久免费的开源 BI 工具!
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步